Measurement and Geometry - HiSet: High School Equivalency Test: Math
Card 0 of 20
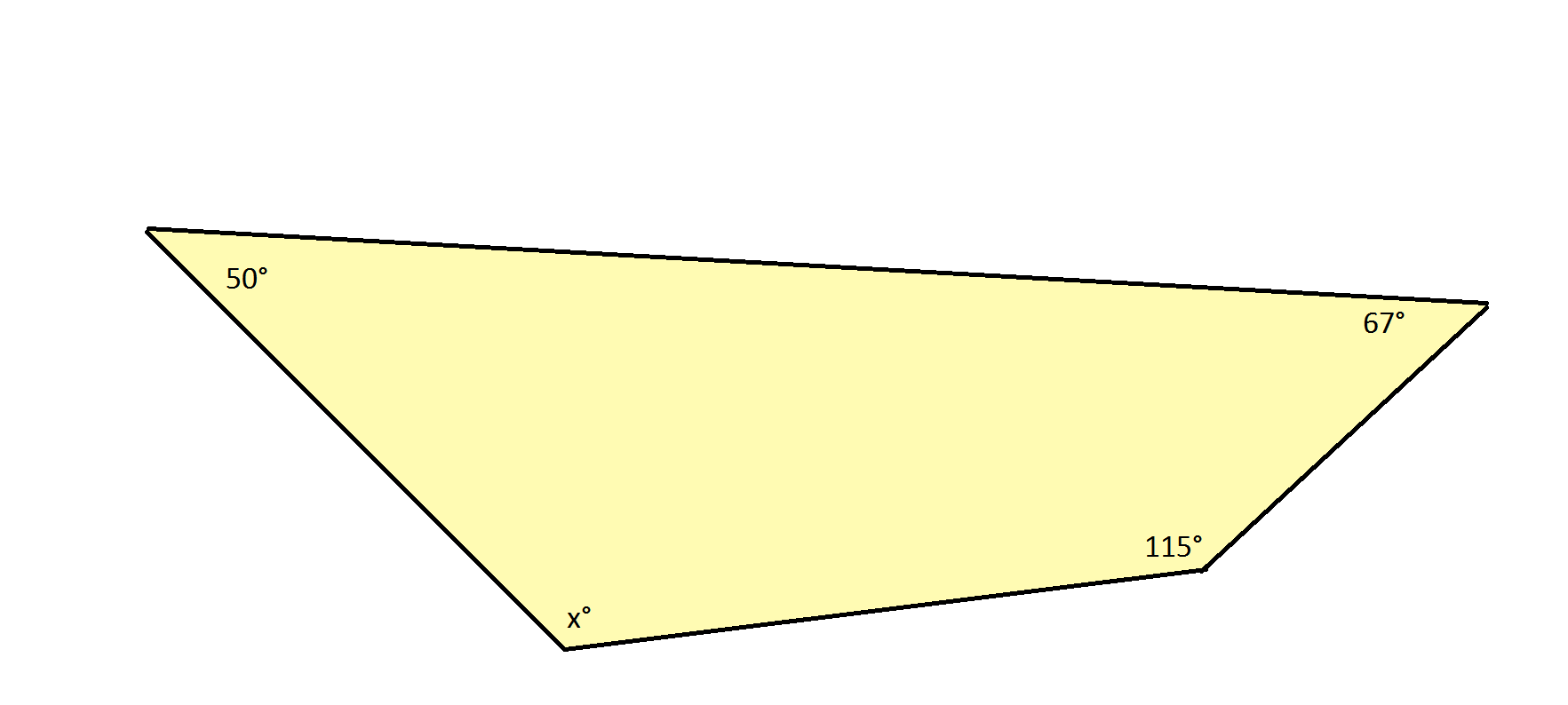
A quadrilateral is shown, and the angle measures of 3 interior angles are given. Find x, the missing angle measure.

A quadrilateral is shown, and the angle measures of 3 interior angles are given. Find x, the missing angle measure.
The sum of the measures of the interior angles of a quadrilateral is 360 degrees. The sum of the measures of the interior angles of any polygon can be determined using the following formula:
 , where
, where  is the number of sides.
is the number of sides.
For example, with a quadrilateral, which has 4 sides, you obtain the following calculation:

Solving for  requires setting up an algebraic equation, adding all 4 angles to equal 360 degrees:
requires setting up an algebraic equation, adding all 4 angles to equal 360 degrees:

Solving for  is straightforward: subtract the values of the 3 known angles from both sides:
is straightforward: subtract the values of the 3 known angles from both sides:


The sum of the measures of the interior angles of a quadrilateral is 360 degrees. The sum of the measures of the interior angles of any polygon can be determined using the following formula:


For example, with a quadrilateral, which has 4 sides, you obtain the following calculation:
Solving for 
Solving for 
Compare your answer with the correct one above
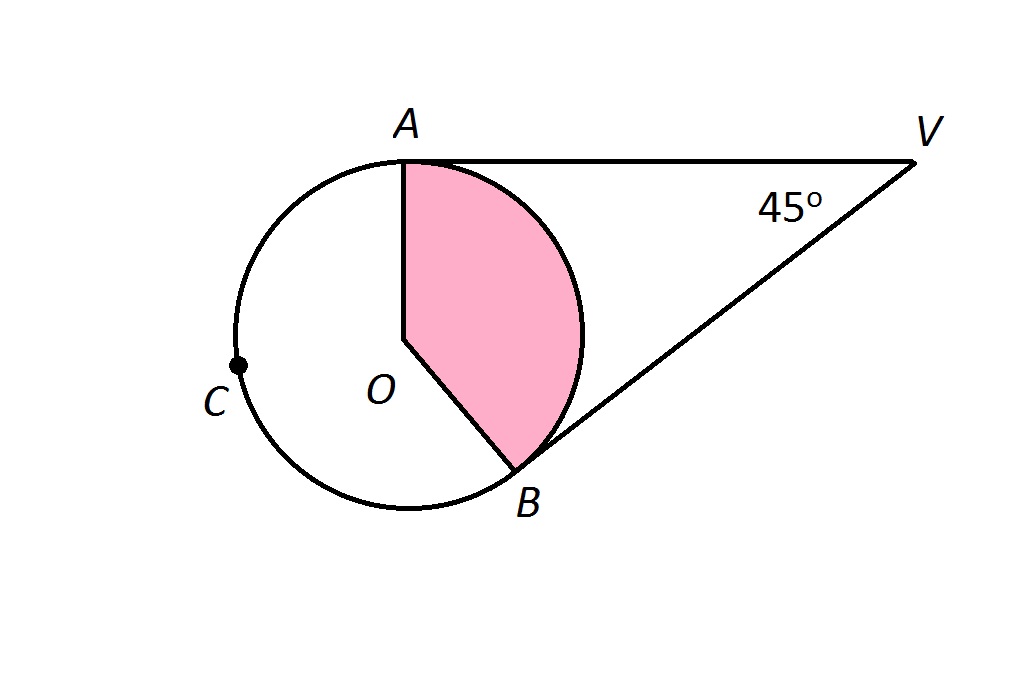
 is the center of the above circle. Calculate
is the center of the above circle. Calculate  .
.



 is the central angle that intercepts
is the central angle that intercepts  , so
, so
 .
.
Therefore, we need to find  to obtain our answer.
to obtain our answer.
If the sides of an angle with vertex outside the circle are both tangent to the circle, the angle formed is half the difference of the measures of the arcs. Therefore,

Letting  , since the total arc measure of a circle is 360 degrees,
, since the total arc measure of a circle is 360 degrees,

We are also given that

Making substitutions, and solving for  :
:


Multiply both sides by 2:


Subtract 360 from both sides:


Divide both sides by  :
:

 ,
,
the measure of  and, consequently, that of
and, consequently, that of  .
.



Therefore, we need to find 
If the sides of an angle with vertex outside the circle are both tangent to the circle, the angle formed is half the difference of the measures of the arcs. Therefore,
Letting 
We are also given that
Making substitutions, and solving for 
Multiply both sides by 2:
Subtract 360 from both sides:
Divide both sides by 

the measure of 

Compare your answer with the correct one above

The above figure shows a regular seven-sided polygon, or heptagon, inscribed inside a circle.  is the common center of the figures.
is the common center of the figures.
Give the measure of  .
.

The above figure shows a regular seven-sided polygon, or heptagon, inscribed inside a circle. 
Give the measure of 
Consider the figure below, which adds some radii of the heptagon (and circle):

 , as a radius of a regular polygon, bisects
, as a radius of a regular polygon, bisects  . The measure of this angle can be calculated using the formula
. The measure of this angle can be calculated using the formula
 ,
,
where  :
:

Consequently,
 ,
,
the correct response.
Consider the figure below, which adds some radii of the heptagon (and circle):




where 
Consequently,

the correct response.
Compare your answer with the correct one above

The above figure shows a regular seven-sided polygon, or heptagon, inscribed inside a circle.  is the common center of the figures.
is the common center of the figures.
Give the measure of  .
.

The above figure shows a regular seven-sided polygon, or heptagon, inscribed inside a circle. 
Give the measure of 
Examine the diagram below, which divides  into three congruent angles, one of which is
into three congruent angles, one of which is  :
:

The measure of a central angle of a regular  -sided polygon which intercepts one side of the polygon is
-sided polygon which intercepts one side of the polygon is  ; setting
; setting  , the measure of
, the measure of  is
is
 .
.  has measure three times this; that is,
has measure three times this; that is,

Examine the diagram below, which divides 


The measure of a central angle of a regular 





Compare your answer with the correct one above

The above figure shows a regular seven-sided polygon, or heptagon, inscribed inside a circle.  is the common center of the figures.
is the common center of the figures.
Give the measure of  .
.

The above figure shows a regular seven-sided polygon, or heptagon, inscribed inside a circle. 
Give the measure of 
Examine the diagram below, which divides  into two congruent angles, one of which is
into two congruent angles, one of which is  :
:

The measure of a central angle of a regular  -sided polygon which intercepts one side of the polygon is
-sided polygon which intercepts one side of the polygon is  ; setting
; setting  , the measure of
, the measure of  is
is
 .
.  has measure twice this; that is,
has measure twice this; that is,

Examine the diagram below, which divides 


The measure of a central angle of a regular 





Compare your answer with the correct one above

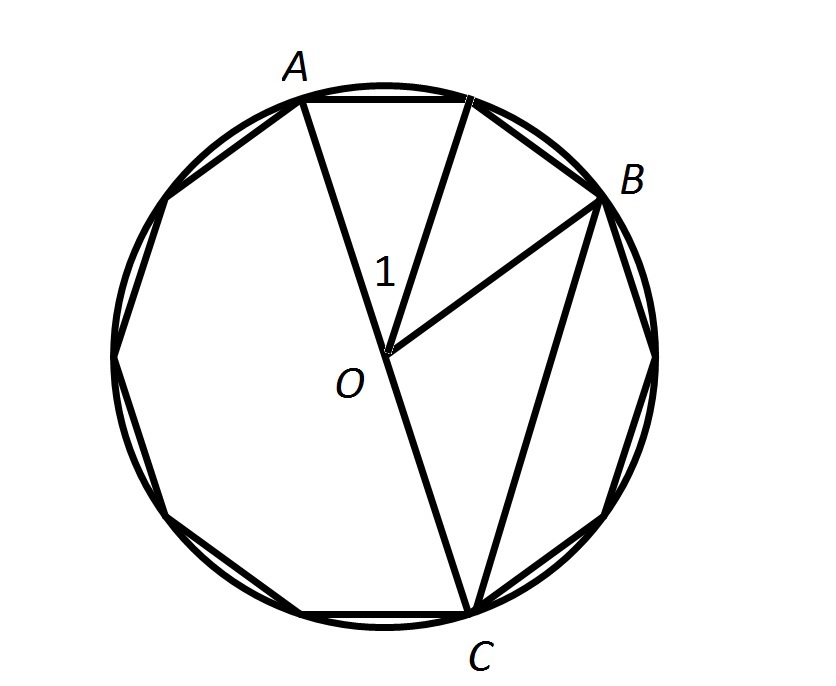
The above figure shows a regular ten-sided polygon, or decagon, inscribed inside a circle.  is the common center of the figures.
is the common center of the figures.
Give the measure of  .
.

The above figure shows a regular ten-sided polygon, or decagon, inscribed inside a circle. 
Give the measure of 
Examine the diagram below, which divides  into two congruent angles, one of which is
into two congruent angles, one of which is  :
:
The measure of a central angle of a regular  -sided polygon which intercepts one side of the polygon is
-sided polygon which intercepts one side of the polygon is  ; setting
; setting  , the measure of
, the measure of  is
is
 .
.  has measure twice this; that is,
has measure twice this; that is,
 .
.
Examine the diagram below, which divides 


The measure of a central angle of a regular 






Compare your answer with the correct one above

The above figure shows a regular ten-sided polygon, or decagon, inscribed inside a circle.  is the common center of the figures.
is the common center of the figures.
Give the measure of  .
.

The above figure shows a regular ten-sided polygon, or decagon, inscribed inside a circle. 
Give the measure of 
Consider the triangle  . Since
. Since  and
and  are radii, they are congruent, and by the Isosceles Triangle Theorem,
are radii, they are congruent, and by the Isosceles Triangle Theorem,  .
.
Now, examine the figure below, which divides  into three congruent angles, one of which is
into three congruent angles, one of which is  :
:

The measure of a central angle of a regular  -sided polygon which intercepts one side of the polygon is
-sided polygon which intercepts one side of the polygon is  ; setting
; setting  , the measure of
, the measure of  is
is
 .
.  has measure three times this; that is,
has measure three times this; that is,
 .
.
The measures of the interior angles of a triangle total  , so
, so

Substituting 108 for  and
and  for
for  :
:






Consider the triangle 



Now, examine the figure below, which divides 


The measure of a central angle of a regular 






The measures of the interior angles of a triangle total 
Substituting 108 for 


Compare your answer with the correct one above

The above figure shows a regular ten-sided polygon, or decagon, inscribed inside a circle.  is the common center of the figures.
is the common center of the figures.
Give the measure of  .
.

The above figure shows a regular ten-sided polygon, or decagon, inscribed inside a circle. 
Give the measure of 
Through symmetry, it can be seen that Quadrilateral  is a trapezoid, such that
is a trapezoid, such that  . By the Same-Side Interior Angle Theorem,
. By the Same-Side Interior Angle Theorem,  and
and  are supplementary - that is,
are supplementary - that is,
 .
.
The measure of  can be calculated using the formula
can be calculated using the formula
 ,
,
where  :
:

Substituting:



Through symmetry, it can be seen that Quadrilateral 




The measure of 

where 
Substituting:
Compare your answer with the correct one above
If two angles are supplementary and one angle measures  , what is the measurement of the second angle?
, what is the measurement of the second angle?
If two angles are supplementary and one angle measures 
Step 1: Define supplementary angles. Supplementary angles are two angles whose sum is  .
.
Step 2: Find the other angle by subtracting the given angle from the maximum sum of the two angles.
So, 
The missing angle (or second angle) is 
Step 1: Define supplementary angles. Supplementary angles are two angles whose sum is 
Step 2: Find the other angle by subtracting the given angle from the maximum sum of the two angles.
So,
The missing angle (or second angle) is
Compare your answer with the correct one above
 and
and  are complementary angles.
are complementary angles.
 and
and  are supplementary angles.
are supplementary angles.


Evaluate  .
.




Evaluate 
 and
and  are supplementary angles, so, by definition,
are supplementary angles, so, by definition,

 , so substitute and solve for
, so substitute and solve for  :
:



 and
and  are complementary angles, so, by definition,
are complementary angles, so, by definition,

Substitute and solve for  :
:



 - that is, the angles have the same measure. Therefore,
- that is, the angles have the same measure. Therefore,
 .
.






Substitute and solve for 


Compare your answer with the correct one above
 and
and  are a pair of vertical angles.
are a pair of vertical angles.
 and
and  are a linear pair.
are a linear pair.
 and
and  are the two acute angles of a right triangle.
are the two acute angles of a right triangle.
Which of the following must be true?






Which of the following must be true?
 and
and  are a pair of vertical angles; it follows that
are a pair of vertical angles; it follows that

 and
and  are a linear pair; it follows that they are supplementary - that is,
are a linear pair; it follows that they are supplementary - that is,
 .
.
 and
and  are the two acute angles of a right triangle; it follows that they are complementary - that is,
are the two acute angles of a right triangle; it follows that they are complementary - that is,
 .
.
Therefore, we have the three statements



From the second statement, we can subtract  from both sides to get
from both sides to get


Substitute this expression for  in the third expression to get
in the third expression to get

Substitute  for
for  :
:

Add  to both sides:
to both sides:

 ,
,
or, rearranged,
 .
.








Therefore, we have the three statements
From the second statement, we can subtract 
Substitute this expression for 
Substitute 

Add 

or, rearranged,

Compare your answer with the correct one above
Find the length of the hypotenuse of a right triangle whose legs are the following lengths:

Find the length of the hypotenuse of a right triangle whose legs are the following lengths:
The hypotenuse of a right triangle can be calculated using the Pythagorean Theorem. This theorem states that if we know the lengths of the two other legs of the triangle, then we can calculate the hypotenuse. It is written in the following way:

In this formula the legs are noted by the variables,  and
and  . The variable
. The variable  represents the hypotenuse.
represents the hypotenuse.
Substitute and solve for the hypotenuse.

Simplify.


Take the square root of both sides of the equation.


The hypotenuse of a right triangle can be calculated using the Pythagorean Theorem. This theorem states that if we know the lengths of the two other legs of the triangle, then we can calculate the hypotenuse. It is written in the following way:
In this formula the legs are noted by the variables, 


Substitute and solve for the hypotenuse.
Simplify.
Take the square root of both sides of the equation.
Compare your answer with the correct one above
If the two legs of a right triangle are  cm and
cm and  cm, what is the length of the hypotenuse. Answer must be in SIMPLIFIED form (or lowest terms).
cm, what is the length of the hypotenuse. Answer must be in SIMPLIFIED form (or lowest terms).
If the two legs of a right triangle are 

Step 1: Recall the Pythagorean theorem statement and formula.
Statement: For any right triangle, the sums of the squares of the shorter sides is equal to the square of the longest side.
Formula: In a right triangle  , If
, If  are the shorter sides and
are the shorter sides and  is the longest side.. then,
is the longest side.. then,

Step 2: Plug in the values given to us in the problem....

Evaluate:

Simplify:

Simplify:

Take the square root...

Step 3: Simplify the root...

The length of the hypotenuse in most simplified form is  cm.
cm.
Step 1: Recall the Pythagorean theorem statement and formula.
Statement: For any right triangle, the sums of the squares of the shorter sides is equal to the square of the longest side.
Formula: In a right triangle 


Step 2: Plug in the values given to us in the problem....
Evaluate:
Simplify:
Simplify:
Take the square root...
Step 3: Simplify the root...
The length of the hypotenuse in most simplified form is 
Compare your answer with the correct one above
Which of the following could be the lengths of the sides of a right triangle?
Which of the following could be the lengths of the sides of a right triangle?
In each choice, the two shortest sides of the triangle are 9 and 12, so the third side can be found by applying the Pythagorean Theorem. Set  in the Pythagorean equation and solve for
in the Pythagorean equation and solve for  :
:

Take the square root:
 .
.
The correct choice is
 .
.
In each choice, the two shortest sides of the triangle are 9 and 12, so the third side can be found by applying the Pythagorean Theorem. Set 

Take the square root:

The correct choice is

Compare your answer with the correct one above

The depicted circle has a radius of 3 cm. The arc length between the two points shown on the circle is  cm. Find the area of the enclosed sector (highlighted in green).
cm. Find the area of the enclosed sector (highlighted in green).

The depicted circle has a radius of 3 cm. The arc length between the two points shown on the circle is 
First, find the area and circumference of the circle using the radius and the following formulae for circles:


Substituting in 3 for  yields:
yields:


Next, find what fraction of the total circumference is between the two points on the circle (the arc length).

Finally, use this fraction to calculate the area of the enclosed sector. Note that this area is proportional to the above fraction. In other words:

So the Sector Area is one sixth of the total area.

Cross multiply:

Divide both sides by 6, then simplify to get the final answer:

First, find the area and circumference of the circle using the radius and the following formulae for circles:
Substituting in 3 for 
Next, find what fraction of the total circumference is between the two points on the circle (the arc length).
Finally, use this fraction to calculate the area of the enclosed sector. Note that this area is proportional to the above fraction. In other words:
So the Sector Area is one sixth of the total area.
Cross multiply:
Divide both sides by 6, then simplify to get the final answer:
Compare your answer with the correct one above

 is the center of the above circle, and
is the center of the above circle, and  . Evaluate the length of
. Evaluate the length of  .
.




The radius of the circle is given to be  . The total circumference
. The total circumference  of the circle is
of the circle is  times this, or
times this, or
 .
.
The length  of
of  is equal to
is equal to

Thus, it is first necessary to find the degree measure of  . If the sides of an angle with vertex outside the circle are both tangent to the circle, the angle formed is half the difference of the measures of the arcs. Therefore,
. If the sides of an angle with vertex outside the circle are both tangent to the circle, the angle formed is half the difference of the measures of the arcs. Therefore,

Letting  , since the total arc measure of a circle is 360 degrees,
, since the total arc measure of a circle is 360 degrees,

We are also given that

Making substitutions, and solving for  :
:


Multiply both sides by 2:


Subtract 360 from both sides:


Divide both sides by  :
:

 ,
,
the degree measure of  .
.
Thus, the length  of
of  is
is





The radius of the circle is given to be 



The length 

Thus, it is first necessary to find the degree measure of 
Letting 
We are also given that
Making substitutions, and solving for 
Multiply both sides by 2:
Subtract 360 from both sides:
Divide both sides by 

the degree measure of 
Thus, the length 

Compare your answer with the correct one above

 is the center of the above circle, and
is the center of the above circle, and  . Evaluate the area of the shaded sector.
. Evaluate the area of the shaded sector.



The radius of the circle is given to be  . The total area
. The total area  of the circle can be found using the area formula:
of the circle can be found using the area formula:



The area  of the sector is equal to
of the sector is equal to

Thus, it is first necessary to find the degree measure of  . If the sides of an angle with vertex outside the circle are both tangent to the circle, the angle formed is half the difference of the measures of the arcs. Therefore,
. If the sides of an angle with vertex outside the circle are both tangent to the circle, the angle formed is half the difference of the measures of the arcs. Therefore,

Letting  , since the total arc measure of a circle is 360 degrees,
, since the total arc measure of a circle is 360 degrees,

We are also given that

Making substitutions, and solving for  :
:


Multiply both sides by 2:


Subtract 360 from both sides:


Divide both sides by  :
:

 ,
,
the degree measure of  .
.
Thus, the area of the shaded sector is





The radius of the circle is given to be 

The area 
Thus, it is first necessary to find the degree measure of 
Letting 
We are also given that
Making substitutions, and solving for 
Multiply both sides by 2:
Subtract 360 from both sides:
Divide both sides by 

the degree measure of 
Thus, the area of the shaded sector is
Compare your answer with the correct one above

 is the center of the above circle, and
is the center of the above circle, and  . Evaluate the area of the shaded sector.
. Evaluate the area of the shaded sector.



The radius of the circle is given to be  . The total area
. The total area  of the circle can be found using the area formula:
of the circle can be found using the area formula:



The area  of the sector is equal to
of the sector is equal to

Thus, it is first necessary to find the degree measure of  . If the sides of an angle with vertex outside the circle are both tangent to the circle, the angle formed is half the difference of the measures of the arcs. Therefore,
. If the sides of an angle with vertex outside the circle are both tangent to the circle, the angle formed is half the difference of the measures of the arcs. Therefore,

Letting  , since the total arc measure of a circle is 360 degrees,
, since the total arc measure of a circle is 360 degrees,

We are also given that

Making substitutions, and solving for  :
:


Multiply both sides by 2:


Add 360 to both sides:


Divide both sides by 2:

 ,
,
the degree measure of  .
.
Therefore, the area  of the shaded sector is
of the shaded sector is





The radius of the circle is given to be 

The area 
Thus, it is first necessary to find the degree measure of 
Letting 
We are also given that
Making substitutions, and solving for 
Multiply both sides by 2:
Add 360 to both sides:
Divide both sides by 2:

the degree measure of 
Therefore, the area 
Compare your answer with the correct one above

 is the center of the above circle, and
is the center of the above circle, and  . Evaluate the length of
. Evaluate the length of  .
.




The radius of the circle is given to be  .
.
The total circumference  of the circle is
of the circle is  times this, or
times this, or
 .
.
The length  of
of  is equal to
is equal to

Thus, it is first necessary to find the degree measure of  . If the sides of an angle with vertex outside the circle are both tangent to the circle, the angle formed is half the difference of the measures of the arcs. Therefore,
. If the sides of an angle with vertex outside the circle are both tangent to the circle, the angle formed is half the difference of the measures of the arcs. Therefore,

Letting  , since the total arc measure of a circle is 360 degrees,
, since the total arc measure of a circle is 360 degrees,

We are also given that

Making substitutions, and solving for  :
:


Multiply both sides by 2:


Add 360 to both sides:


Divide both sides by 2:

 ,
,
the degree measure of  .
.
Thus, the length  of
of  is
is





The radius of the circle is given to be 
The total circumference 


The length 

Thus, it is first necessary to find the degree measure of 
Letting 
We are also given that
Making substitutions, and solving for 
Multiply both sides by 2:
Add 360 to both sides:
Divide both sides by 2:

the degree measure of 
Thus, the length 

Compare your answer with the correct one above

Refer to the above figure. Give the ratio of the area of Sector 2 to that of Sector 1.

Refer to the above figure. Give the ratio of the area of Sector 2 to that of Sector 1.
The ratio of the area of the larger Sector 2 to that of smaller Sector 1 is equal to the ratio of their respective arc measures - that is,
 .
.
Therefore, it is sufficient to find these arc measures.
If the sides of an angle with vertex outside the circle are both tangent to the circle, the angle formed is half the difference of the measures of the arcs. Therefore,

Letting  , since the total arc measure of a circle is 360 degrees,
, since the total arc measure of a circle is 360 degrees,

We are also given that

Making substitutions, and solving for  :
:


Multiply both sides by 2:


Add 360 to both sides:


Divide both sides by 2:

 ,
,
the degree measure of  .
.
It follows that

By the Arc Addition Principle,

Since  , the central angle which intercepts
, the central angle which intercepts  , is a right angle,
, is a right angle,  . By substitution,
. By substitution,
 ,
,
and


The ratio  is equal to
is equal to
 ,
,
a 5 to 1 ratio.
The ratio of the area of the larger Sector 2 to that of smaller Sector 1 is equal to the ratio of their respective arc measures - that is,

Therefore, it is sufficient to find these arc measures.
If the sides of an angle with vertex outside the circle are both tangent to the circle, the angle formed is half the difference of the measures of the arcs. Therefore,
Letting 
We are also given that
Making substitutions, and solving for 
Multiply both sides by 2:
Add 360 to both sides:
Divide both sides by 2:

the degree measure of 
It follows that
By the Arc Addition Principle,
Since 



and
The ratio 

a 5 to 1 ratio.
Compare your answer with the correct one above











































































































































