Functions and function notation - HiSet: High School Equivalency Test: Math

Card 0 of 17

Question

Define functions $f(x) = \sqrt{x}$ and $g(x) =- x^{2}$

Give the domain of the composition $g\circ f$ .

Answer

The domain of the composition of functions $g\circ f$ is that the set of all values that fall in the domain of such that falls in the domain of .

$f(x) = \sqrt{x}$ , a square root function, whose domain is the set of all values of that make the radicand nonnegative. Since the radicand is itself, the domain of is simply the set of all nonnegative numbers, or $\left [ 0, \infty\right )$ .

$g(x) =- x^{2}$ , a polynomial function, whose domain is the set of all real numbers. Therefore, the domain is not restricted further by . The domain of $g\circ f$ is $\left [ 0, \infty\right )$ .

Compare your answer with the correct one above

Question

Define functions $f(x) = \sqrt{x}$ and $g(x) =- x^{2}$

Give the domain of the composition $f \circ g$ .

Answer

The domain of the composition of functions $f \circ g$ is the set of all values that fall in the domain of such that falls in the domain of .

$g(x) =- x^{2}$ , a polynomial function, so the domain of is equal to the set of all real numbers, $\left ( -\infty, \infty\right )$ . Therefore, places no restrictions on the domain of $f \circ g$ .

$f(x) = \sqrt{x}$ , a square root function, whose domain is the set of all values of that make the radicand nonnegative. Since the radicand is itself, the domain of is simply the set of all nonnegative numbers, or $\left [ 0, \infty\right )$ . Therefore, we must select the set of all in $\left ( -\infty, \infty\right )$ such that $g(c) \ge 0$ , or, equivalently,

$-c^{2} \ge 0$

However, $c^{2} \ge 0$ , so $-c^{2} \le 0$ , with equality only if . Therefore, the domain of $f \circ g$ is the single-element set $\left { 0 \right }$ , which is not among the choices.

Compare your answer with the correct one above

Question

Define functions $f(x) = \frac{1}{x-1}$ and $g(x)= \sqrt{x}+ 1$ .

Give the domain of the composition $g\circ f$ .

Answer

The domain of the composition of functions $g\circ f$ is that the set of all values that fall in the domain of such that falls in the domain of .

$f(x) = \frac{1}{x-1}$ , a rational function, so its domain is the set of all numbers except those that make its denominator zero. if and only if , making its domain $(-\infty, 1) \cup (1, \infty)$ .

$g(x)= \sqrt{x}+ 1$ , a square root function, so the domain of is the set of all values that make the radicand a nonnegative number. Since the radicand is itself, the domain of is simply the set of all nonnegative numbers, or $\left [ 0, \infty\right )$ .

Therefore, we need to further restrict the domain to those values in $(-\infty, 1) \cup (1, \infty)$ that make

$f(c) \ge 0$

Equivalently,

$\frac{1}{c-1}\ge 0$

Since 1 is positive, and the quotient is nonnegative as well, it follows that

,

and

.

The domain of $g\circ f$ is therefore $(1, \infty)$ .

Compare your answer with the correct one above

Question

Define functions $f(x) = \frac{1}{x-1}$ and $g(x)= \sqrt{x}+ 1$ .

Give the domain of the composition $f \circ g$ .

Answer

The domain of the composition of functions $f \circ g$ is the set of all values that fall in the domain of such that falls in the domain of .

$g(x)= \sqrt{x}+ 1$ , a square root function, so the domain of is the set of all values that make the radicand a nonnegative number. Since the radicand is itself, the domain of is simply the set of all nonnegative numbers, or $\left [ 0, \infty\right )$ .

$f(x) = \frac{1}{x-1}$ , a rational function, so its domain is the set of all numbers except those that make its denominator zero. if and only if , so from $\left [ 0, \infty\right )$ , we exclude only the value so that

;

that is,

$\sqrt{c}+ 1 = 1$

$\sqrt{c}+ 1 - 1 = 1 - 1$

$\sqrt{c} = 0$

Excluding this value from the domain, this leaves $\left ( 0, \infty\right )$ as the domain of $f \circ g$ .

Compare your answer with the correct one above

Question

Define functions $f(x) = x^{2}-16$ and $g(x) = \sqrt{x}$ .

Give the domain of the composition $g\circ f$ .

Answer

The domain of the composition of functions $g\circ f$ is that the set of all values that fall in the domain of such that falls in the domain of .

$f(x) = x^{2}-16$ , a polynomial function, so its domain is the set of all real numbers.

$g(x) = \sqrt{x}$ , so the domain of is the set of all values that make the radicand a nonnegative number. Since the radicand is itself, the domain of is simply the set of all nonnegative numbers, or $\left [ 0, \infty\right )$ .

Therefore, the domain of $g\circ f$ is the set of all real numbers such that

$f(c) \ge 0$ .

Equivalently,

$c^{2}-16 \ge 0$

To solve this, first, solve the corresponding equation:

$c^{2}-16 = 0$

Factor the polynomial at left using the difference of squares pattern:

By the Zero Factor Property, either

, in which case ,

or

, in which case .

These are the boundary values of the intervals to be tested. Choose an interior value of each interval and test it in the inequality:

$(-\infty, -4)$

Testing :

$(-5)^{2}-16 \ge 0$

$25-16 \ge 0$

$9 \ge 0$ - True; include

Testing :

$0^{2}-16 \ge 0$

$0 -16 \ge 0$

$-16 \ge 0$ - False; exclude

$( 4 , \infty)$

Testing :

$5^{2}-16 \ge 0$

$25-16 \ge 0$

$9 \ge 0$ - True; include

Include $(-\infty, -4)$ and $( 4 , \infty)$ . Also include the boundary values, since equality is included in the inequality statement ( $\ge$ ).

The correct domain is $(-\infty, -4] \cup [4 , \infty)$ .

Compare your answer with the correct one above

Question

Define functions $f(x) = x^{2}-16$ and $g(x) = \sqrt{x}$ .

Give the domain of the composition $f \circ g$ .

Answer

The domain of the composition of functions $f \circ g$ is the set of all values that fall in the domain of such that falls in the domain of .

$g(x) = \sqrt{x}$ , a square root function, so the domain of is the set of all values that make the radicand a nonnegative number. Since the radicand is itself, the domain of is simply the set of all nonnegative numbers, or $\left [ 0, \infty\right )$ .

$f(x) = x^{2}-16$ , a polynomial function; its domain is the set of all reals, so it does not restrict the domain any further.

The correct domain is $\left [ 0, \infty\right )$ .

Compare your answer with the correct one above

Question

Define functions $f(x) = \sqrt{x-8}$ and $g(x) = \sqrt{x+ 8}$ .

Give the domain of the function .

Answer

The domain of the sum of two functions is the intersections of the domains of the individual functions. Both and are square root functions, so their radicands must both be positive.

The domain of is the set of all values of such that:

$x-8 \ge 0$

Adding 8 to both sides:

$x-8 + 8 \ge 0 + 8$

$x \ge 8$

This domain is $[8, \infty )$ .

The domain of is the set of all values of such that:

$x+8 \ge 0$

Subtracting 8 tfrom both sides:

$x+ 8-8 \ge 0 - 8$

$x \ge -8$

This domain is $[-8, \infty )$

The domain of is the intersection of the domains, which is $[8, \infty )$ .

Compare your answer with the correct one above

Question

Define functions $f(x) = \sqrt{x+8}$ and $g(x) = \sqrt{8-x}$ .

Give the domain of the function .

Answer

The domain of the difference of two functions is the intersections of the domains of the individual functions. Both and are square root functions, so their radicands must both be positive.

The domain of is the set of all values of such that:

$x+8 \ge 0$

Subtracting 8 tfrom both sides:

$x+ 8-8 \ge 0 - 8$

$x \ge -8$

This domain is $[-8, \infty )$

The domain of is the set of all values of such that:

$8-x \ge 0$

Adding to both sides:

$8-x + x \ge 0 + x$

$8 \ge x$ , or

$x \le 8$

This domain is $(-\infty , 8]$ .

The domain of is the intersection of these, .

Compare your answer with the correct one above

Question

Define functions $f(x) = \sqrt[3]{x-8}$ and $g(x) = \sqrt[3]{x+ 8}$ .

Give the domain of the function .

Answer

The domain of the sum of two functions is the intersections of the domains of the individual functions.

Both and are cube root functions. There is no restriction on the value of the radicand of a cube root, so both of these functions have as their domain the set of all real numbers $(-\infty, \infty)$ . It follows that also has domain $(-\infty, \infty)$ .

Compare your answer with the correct one above

Question

Define

$f(x)= \left{\begin{matrix} x-2,&x< 0 \ x+ 3,& x \ge 0\end{matrix}\right.$

Give the range of the function.

Answer

The range of a function is the set of all possible values of over its domain.

Since this function is piecewise-defined, it is necessary to examine both parts of the function and extract the range of each.

For , it holds that , so

,

or

$x \in(-\infty, -2)$ .

For $x \ge 0$ , it holds that , so

$x \ge 0$

$x+ 3 \ge 0+ 3$

$f(x) \ge 3$ ,

or

$x \in [3, \infty)$

The overall range of is the union of these sets, or $(-\infty, -2) \cup [3, \infty)$ .

Compare your answer with the correct one above

Question

Define $f(x)= -\frac{1}{x+1}$ and .

Evaluate $(f\circ g )(2)$ .

Answer

By definition,

$(f\circ g )(2) = f(g(2))$ ,

so first, evaluate by substituting 2 for in :

$(f\circ g )(2) = f(4)$ ,

so evaluate through a similar substitution:

$f(x)= -\frac{1}{x+1}$

$f(4)= -\frac{1}{4+1} = - \frac{1}{5}$ ,

the correct response.

Compare your answer with the correct one above

Question

Define functions and as follows:

$f(x)= \left{\begin{matrix} x^{2} -2,&x< 0 \ x+ 3,& x \ge 0\end{matrix}\right.$

Evaluate $(f \circ g)(0)$ .

Answer

By definition, $(f \circ g)(0) = f(g(0))$ . Evaluate by substituting 0 for in the definition of :

$(f \circ g)(0) = f(g(0)) = f(4)$ , so substitute 4 for in the definition of . Since 4 satisfies the condition $x \ge 0$ , use the definition for those values:

,

the correct value.

Compare your answer with the correct one above

Question

The plot shows the graphs of five different equations. Using shape and location, determine which graphed line corresponds to the equation .

Answer

The power of and are both 1, so this is a linear equation of order 1. Therefore, the graph must be a straight line. We can eliminate A and E, since neither are straight lines.

The equation is given in the slope-intercept form, , where stands for the slope of the line and stands for the line's y-intercept. Since , the coefficient of x, is positive here, we are looking for a line that goes upwards. We can eliminate D since it goes downwards, and therefore has a negative slope.

In the given equation, the constant , which represents the y-intercept, is also positive. Therefore, the line we are looking for also must intersect the y-axis at a positive value. The graph C appears to intersect the y-axis at a negative value, whereas the graph B appears to intersect the y-axis at a positive value. Therefore, B is the corresponding graph.

Compare your answer with the correct one above

Question

A restaurant sets the prices of its dishes using the following function:

Price = (Cost of Ingredients) + (40% of the Cost of Ingredients) + 5

where all quantities are in U.S. Dollars.

If the cost of ingredients for a steak dish is $14, what will the restaurant set the price of the steak dish at?

Answer

The price of the dish is a function of a single variable, the cost of the ingredients. One way to conceptualize the problem is by thinking of it in function notation. Let be the variable representing the cost of the ingredients. Let be a function of the cost of ingredients giving the price of the dish. Then, we can turn

"Price = (Cost of Ingredients) + (40% of the Cost of Ingredients) + 5"

into a regular equation with recognizable parts. Replace "Price" with and replace "cost of ingredients" with the variable .

Simplify by combining like terms ( and ) to obtain:

The cost of ingredients for the steak dish is $14, so substitute 14 for .

$p(14) = 1.4\times14 +5$

All that's left is to compute the answer:

So, the steak dish will have a price of $24.60.

Compare your answer with the correct one above

Question

The daily pay in U.S. Dollars for a certain job is defined as the following function , where equals time in hours:

If an employee works for 7 hours in a day, how much is he or she paid?

Answer

The above function can be understood as, "An employee is paid $15 for each hour he or she works, plus a flat amount of $10."

If an employee works 7 hours, we can find the amount that he or she is paid by plugging in 7 for "Hours" in the equation:

Adhering to order of operations, we next find the product of 15 and 7:

Finally, we find the sum of 105 and 10:

The employee is paid $115.00 for seven hours' work.

Compare your answer with the correct one above

Question

Consider the scenario below:

Helen is a painter. It takes her 3 days to make each painting. She has already made 6 paintings. Which of the following functions best models the number of paintings she will have after days?

Answer

The question asks, "Which of the following functions best models the number of paintings she will have after days?"

From this, you know that the variable represents the number of days, and that represents the number of paintings she makes as a function of days spent working.

If it takes 3 days to make a painting, each day results in $\frac{1}{3}$ paintings. Therefore, we have a linear relationship with slope $\frac{1}{3}$ .

Additionally, she begins with 6 paintings. Therefore, even when zero days are spent working on paintings, she will have 6 paintings. In other words, . This means the y-intercept is 6.

As a result, the function will be

$f(x)=\frac{1}{3}x +6$

which can be rewritten as

$f(x)=\frac{x}{3} +6$

Compare your answer with the correct one above

Question

is a linear function defined on the set of real numbers. Four values of are given in the following table:

$\begin{matrix} \underline{x}& \underline{f(x)} \ 13 & 4 \ 10 & 6 \ 7 & 8 \ 4 & 10 \end{matrix}$

Give the definition for .

Answer

By the two-point formula, the equation of a line through points $(x_{1}, y_{1}), (x_{2}, y_{2})$ is

$y-y_{1} = m(x- x_{1})$ ,

where $m = \frac{x_{2}-x_{1}}{y_{2}-y_{1}}$ , the slope of the line. The choice of the two points from the given four is arbitrary, so we will select the middle two ordered pairs. Substituting $x_{1}= 10,y_{1} =6, x_{2}= 7, y_{2}= 8$ , then

$m = \frac{x_{2}-x_{1}}{y_{2}-y_{1}}= \frac{7-10}{8-6} = -\frac{3}{2}$

The first formula becomes

$y-10 = -\frac{3}{2}(x-6)$

Since , solve for . First, distribute $-\frac{3}{2}$ throughout the difference at right:

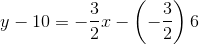
$y-10 = -\frac{3}{2} x- \left (-\frac{3}{2} \right )6$

$y-10 = -\frac{3}{2} x- \left (-9 \right )$

$y-10 = -\frac{3}{2} x+9$

Isolate by adding 10 to both sides:

$y-10+ 10 = -\frac{3}{2} x+9+ 10$

$y = -\frac{3}{2} x+19$

Replacing, the definition of 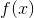is

$f(x) = -\frac{3}{2} x+19$ .

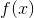
Compare your answer with the correct one above

Tap the card to reveal the answer