Electric Circuits - High School Physics
Card 0 of 20
What is the power of a circuit with a current of  and a resistance of
and a resistance of  ?
?
What is the power of a circuit with a current of 

The standard equation for power is:
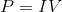
We are given only current and reistance, meaning we must manipulate this equation so that only those variables are present. To do this, we can substitute Ohm's law for voltage.


Now we have an equation for power that uses only current and resistance. Plug in the values given in the question to find the final answer.

The standard equation for power is:
We are given only current and reistance, meaning we must manipulate this equation so that only those variables are present. To do this, we can substitute Ohm's law for voltage.
Now we have an equation for power that uses only current and resistance. Plug in the values given in the question to find the final answer.
Compare your answer with the correct one above
Three capacitors are in series. They have capacitances of  ,
,  , and
, and  , respectively. What is their total capacitance?
, respectively. What is their total capacitance?
Three capacitors are in series. They have capacitances of 


For capacitors in series the formula for total capacitance is:

Note that this formula is similar to the formula for total resistance in parallel. Using the values for each individual capacitor, we can solve for the total capacitance.



For capacitors in series the formula for total capacitance is:
Note that this formula is similar to the formula for total resistance in parallel. Using the values for each individual capacitor, we can solve for the total capacitance.
Compare your answer with the correct one above
Three capacitors are in parallel. They have capacitance values of  ,
,  , and
, and  . What is their total capacitance?
. What is their total capacitance?
Three capacitors are in parallel. They have capacitance values of 


For capacitors in parallel the formula for total capacitance is:

Note that this formula is similar to the formula for total resistance in series. Using the values for each individual capacitor, we can solve for the total capacitance.


For capacitors in parallel the formula for total capacitance is:
Note that this formula is similar to the formula for total resistance in series. Using the values for each individual capacitor, we can solve for the total capacitance.
Compare your answer with the correct one above
Three capacitors, each with a capacity of  are arranged in parallel. What is the total capacitance of this circuit?
are arranged in parallel. What is the total capacitance of this circuit?
Three capacitors, each with a capacity of 
The formula for capacitors in parallel is:

Our three capacitors all have equal capacitance values. We can simply add them together to find the total capacitance.


The formula for capacitors in parallel is:
Our three capacitors all have equal capacitance values. We can simply add them together to find the total capacitance.
Compare your answer with the correct one above
What is the total capacitance of a series circuit with capacitors of  ,
,  , and
, and  ?
?
What is the total capacitance of a series circuit with capacitors of 


The total capacitance of a series circuit is 
Plug in our given values.




The total capacitance of a series circuit is
Plug in our given values.
Compare your answer with the correct one above
Calculate the total capacitance of a circuit with the following three capacitors in parallel.

Calculate the total capacitance of a circuit with the following three capacitors in parallel.
To calculate the total capacitance for capacitors in parallel, simply sum the value of each individual capacitor.


To calculate the total capacitance for capacitors in parallel, simply sum the value of each individual capacitor.
Compare your answer with the correct one above
Calculate the total capacitance of a circuit with the following three capacitors in series.

Calculate the total capacitance of a circuit with the following three capacitors in series.
To find the total capacitance for capacitors in series, we must sum the inverse of each individual capacitance and take the reciprocal of the result.



Remember, you must still take the final reciprocal!

To find the total capacitance for capacitors in series, we must sum the inverse of each individual capacitance and take the reciprocal of the result.
Remember, you must still take the final reciprocal!
Compare your answer with the correct one above
Ten resistors, each with  resistance, are set up in series. What is their equivalent resistance?
resistance, are set up in series. What is their equivalent resistance?
Ten resistors, each with 
For resistors aligned in series, the equivalent resistance is the sum of the individual resistances.

Since all the resistors in this problem are equal, we can simplify with multiplication.


For resistors aligned in series, the equivalent resistance is the sum of the individual resistances.
Since all the resistors in this problem are equal, we can simplify with multiplication.
Compare your answer with the correct one above
Ten resistors, each with  resistance, are set up in parallel. What is the equivalent resistance?
resistance, are set up in parallel. What is the equivalent resistance?
Ten resistors, each with 
For resistors in parallel, the equivalent resistance can be found by summing the reciprocals of the individual resistances, then taking the reciprocal of the resultant sum.

Since all the resistors in this problem are equal, we can simplify by multiplying.




For resistors in parallel, the equivalent resistance can be found by summing the reciprocals of the individual resistances, then taking the reciprocal of the resultant sum.
Since all the resistors in this problem are equal, we can simplify by multiplying.
Compare your answer with the correct one above
There are three resistors in parallel in a circuit with resistances of  ,
,  , and
, and  .
.
What is the equivalent resistance?
There are three resistors in parallel in a circuit with resistances of 


What is the equivalent resistance?
The equation for resistors in parallel is:

We are given the values of the resistors. Using this formula, we can solve for the equivalent resistance.
Plug in the given values and solve.





The equation for resistors in parallel is:
We are given the values of the resistors. Using this formula, we can solve for the equivalent resistance.
Plug in the given values and solve.
Compare your answer with the correct one above
Twelve resistors of equal resistance are set up in series. If the total resistance is  , what is the resistance of each resistor?
, what is the resistance of each resistor?
Twelve resistors of equal resistance are set up in series. If the total resistance is 
The total resistance of resistors in series is the sum of the individual resistances.

In this case, we know the total resistance and the number of resistors, and we are told that all resistors are of equal strength. That means we can simplify this problem using multiplication.

We can use the total resistance to solve for the individual value.



The total resistance of resistors in series is the sum of the individual resistances.
In this case, we know the total resistance and the number of resistors, and we are told that all resistors are of equal strength. That means we can simplify this problem using multiplication.
We can use the total resistance to solve for the individual value.
Compare your answer with the correct one above
Three resistors are in a series. They have  ,
,  , and
, and  of resistance respectively. What is the total resistance?
of resistance respectively. What is the total resistance?
Three resistors are in a series. They have 


When working in a series, the total resistance is the sum of the individual resistances.

Use the given values for each individual resistor to solve for the total resistance.


When working in a series, the total resistance is the sum of the individual resistances.
Use the given values for each individual resistor to solve for the total resistance.
Compare your answer with the correct one above
Six resistors are arranged in a series. Their resistances are  ,
,  ,
,  ,
,  ,
,  , and
, and  . What is their total resistance?
. What is their total resistance?
Six resistors are arranged in a series. Their resistances are 





When working in a series, the total resistance is the sum of the individual resistances.

Use the given values for each individual resistor to solve for the total resistance.


When working in a series, the total resistance is the sum of the individual resistances.
Use the given values for each individual resistor to solve for the total resistance.
Compare your answer with the correct one above
Three resistors are in a parallel circuit. They have resistances of  ,
,  , and
, and  , respectively. What is their total resistance?
, respectively. What is their total resistance?
Three resistors are in a parallel circuit. They have resistances of 


The formula for resistors in parallel is:

Using the given individual resistances, we can find the total resistance of the circuit.



The formula for resistors in parallel is:
Using the given individual resistances, we can find the total resistance of the circuit.
Compare your answer with the correct one above
Two resistors in series have  and
and  resistance, respectively. What is the total resistance?
resistance, respectively. What is the total resistance?
Two resistors in series have 

For resistors in a series, total resistance is equal to the sum of each individual resistance.

We can use the individual resistances from the question to solve for the total resistance.


For resistors in a series, total resistance is equal to the sum of each individual resistance.
We can use the individual resistances from the question to solve for the total resistance.
Compare your answer with the correct one above
What is the total resistance of a series circuit with resistors of  ,
,  , and
, and  ?
?
What is the total resistance of a series circuit with resistors of 


For a series circuit, the formula for total resistance is:

We are given the values of each resistance, allowing us to sum them to find the total resistance in the circuit.


For a series circuit, the formula for total resistance is:
We are given the values of each resistance, allowing us to sum them to find the total resistance in the circuit.
Compare your answer with the correct one above
What is the total resistance of a parallel circuit with resistors of  ,
,  , and
, and  ?
?
What is the total resistance of a parallel circuit with resistors of 


The formula for resistance in parallel is:

We are given the values for each individual resistor, allowing us to solve for the total resistance.



The formula for resistance in parallel is:
We are given the values for each individual resistor, allowing us to solve for the total resistance.
Compare your answer with the correct one above
Calculate the resistance of a copper wire with cross-sectional area of  and length of
and length of  .
.

Calculate the resistance of a copper wire with cross-sectional area of 

The resistance of a wire is given by the following equation:

We are given the resistivity ( ), cross-sectional area, and length. Using these values, we can solve for the resistance.
), cross-sectional area, and length. Using these values, we can solve for the resistance.
First, convert the cross-sectional area to square-meters.

Use the resistance equation to solve.


The resistance of a wire is given by the following equation:
We are given the resistivity (
First, convert the cross-sectional area to square-meters.
Use the resistance equation to solve.
Compare your answer with the correct one above
What is the total resistance of a  ,
,  , and
, and  series circuit?
series circuit?
What is the total resistance of a 


The formula for resistors in series is  .
.
Plug in our given values.



The formula for resistors in series is 
Plug in our given values.
Compare your answer with the correct one above

Calculate the voltage drop across the 14 ohm resistor.
Calculate the voltage drop across the 14 ohm resistor.
To begin, let us start with the  resistor and the
resistor and the  resistor that are in parallel. In parallel we can add resistors through the equation
resistor that are in parallel. In parallel we can add resistors through the equation 





This new resistor is now in series with the two 4Ω resistors. In series we can just add these resistors up.


This new resistor is now in parallel with the  resistor. In parallel we can add resistors through the equation
resistor. In parallel we can add resistors through the equation 




This new resistor is now in series with the  and
and  resistor. In series we can just add these resistors up.
resistor. In series we can just add these resistors up.


Now that we have the equivalent resistance of the circuit. We can now determine the current flowing out of the battery.

Rearrange to solve for current.



One of the best ways to work through a problem like this is to create a V= IR chart for all the components of the circuit.

We know that the current that is flowing out of the battery is the current that is flowing through both by 5 and 3 Ohm resistors since all of these are in series. So we can put this information into our chart.

Using Ohm’s Law we can determine the voltage for each of these two resistors.






We can now use Kirchoff’s loop law through the loop of the 5, 3, and 14 Ohm resistor to determine the voltage that is traveling through the 14 Ohm resistor.



To begin, let us start with the 

This new resistor is now in series with the two 4Ω resistors. In series we can just add these resistors up.
This new resistor is now in parallel with the 
This new resistor is now in series with the 

Now that we have the equivalent resistance of the circuit. We can now determine the current flowing out of the battery.
Rearrange to solve for current.
One of the best ways to work through a problem like this is to create a V= IR chart for all the components of the circuit.

We know that the current that is flowing out of the battery is the current that is flowing through both by 5 and 3 Ohm resistors since all of these are in series. So we can put this information into our chart.

Using Ohm’s Law we can determine the voltage for each of these two resistors.

We can now use Kirchoff’s loop law through the loop of the 5, 3, and 14 Ohm resistor to determine the voltage that is traveling through the 14 Ohm resistor.
Compare your answer with the correct one above


























