Circuit Calculations and Concepts - High School Physics
Card 0 of 20
What is the power of a circuit with a current of 
and a resistance of 
?
What is the power of a circuit with a current of
The standard equation for power is:
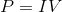
We are given only current and reistance, meaning we must manipulate this equation so that only those variables are present. To do this, we can substitute Ohm's law for voltage.
Now we have an equation for power that uses only current and resistance. Plug in the values given in the question to find the final answer.
The standard equation for power is:
We are given only current and reistance, meaning we must manipulate this equation so that only those variables are present. To do this, we can substitute Ohm's law for voltage.
Now we have an equation for power that uses only current and resistance. Plug in the values given in the question to find the final answer.
Compare your answer with the correct one above
Calculate the voltage drop across the 14 ohm resistor.
Calculate the voltage drop across the 14 ohm resistor.
To begin, let us start with the 
resistor and the 
resistor that are in parallel. In parallel we can add resistors through the equation 
This new resistor is now in series with the two 4Ω resistors. In series we can just add these resistors up.
This new resistor is now in parallel with the 
resistor. In parallel we can add resistors through the equation 
This new resistor is now in series with the 
and 
resistor. In series we can just add these resistors up.
Now that we have the equivalent resistance of the circuit. We can now determine the current flowing out of the battery.
Rearrange to solve for current.
One of the best ways to work through a problem like this is to create a V= IR chart for all the components of the circuit.
We know that the current that is flowing out of the battery is the current that is flowing through both by 5 and 3 Ohm resistors since all of these are in series. So we can put this information into our chart.
Using Ohm’s Law we can determine the voltage for each of these two resistors.
We can now use Kirchoff’s loop law through the loop of the 5, 3, and 14 Ohm resistor to determine the voltage that is traveling through the 14 Ohm resistor.
To begin, let us start with the 
This new resistor is now in series with the two 4Ω resistors. In series we can just add these resistors up.
This new resistor is now in parallel with the 
This new resistor is now in series with the 
Now that we have the equivalent resistance of the circuit. We can now determine the current flowing out of the battery.
Rearrange to solve for current.
One of the best ways to work through a problem like this is to create a V= IR chart for all the components of the circuit.
We know that the current that is flowing out of the battery is the current that is flowing through both by 5 and 3 Ohm resistors since all of these are in series. So we can put this information into our chart.
Using Ohm’s Law we can determine the voltage for each of these two resistors.
We can now use Kirchoff’s loop law through the loop of the 5, 3, and 14 Ohm resistor to determine the voltage that is traveling through the 14 Ohm resistor.
Compare your answer with the correct one above
Calculate the current through the 10 ohm resistor.
Calculate the current through the 10 ohm resistor.
To begin, let us start with the 
resistor and the 
resistor that are in parallel. In parallel we can add resistors through the equation 
This new resistor is now in series with the two 
resistors. In series we can just add these resistors up.
This new resistor is now in parallel with the 
resistor. In parallel we can add resistors through the equation 
This new resistor is now in series with the 
and 
resistor. In series we can just add these resistors up.
Now that we have the equivalent resistance of the circuit. We can now determine the current flowing out of the battery.
Rearrange to solve for current.
One of the best ways to work through a problem like this is to create a V= IR chart for all the components of the circuit.
We know that the current that is flowing out of the battery is the current that is flowing through both by 5 and 3 Ohm resistors since all of these are in series. So we can put this information into our chart.
Using Ohm’s Law we can determine the voltage for each of these two resistors.
We can now use Ohm’s law and our voltage to determine the current going through the 14 Ohm resistor.
Next we can analyze the current in the Junction between the 5, 14 and 4 Ohm resistors. Kirchoff’s laws state that the sum of the current flowing in and out of junction must equal 0.
We have 
flowing in from the 
resistor and 
flowing out to go through the 
resistor.
So the current going through the 4 Ohm resistor is 3 amps. This will be the same for both 4 ohm resistors as both have the same current going into and out of the junctions near them. We can then use this to determine the voltage drop across each of the resistors.
Now let’s add this to our chart.
We can now use Kirchoff’s loop law to determine the voltage across the 10 Ohm resistor. Let’s analyze the loop that goes from the 5, to the 4 to the 10 back through the 4 and then through 3 Ohm resistor.
We can now use Ohm’s Law to determine the current through the 10 Ohm resistor.
To begin, let us start with the 
This new resistor is now in series with the two 
This new resistor is now in parallel with the 
This new resistor is now in series with the 
Now that we have the equivalent resistance of the circuit. We can now determine the current flowing out of the battery.
Rearrange to solve for current.
One of the best ways to work through a problem like this is to create a V= IR chart for all the components of the circuit.
We know that the current that is flowing out of the battery is the current that is flowing through both by 5 and 3 Ohm resistors since all of these are in series. So we can put this information into our chart.
Using Ohm’s Law we can determine the voltage for each of these two resistors.
We can now use Ohm’s law and our voltage to determine the current going through the 14 Ohm resistor.
Next we can analyze the current in the Junction between the 5, 14 and 4 Ohm resistors. Kirchoff’s laws state that the sum of the current flowing in and out of junction must equal 0.
We have 
So the current going through the 4 Ohm resistor is 3 amps. This will be the same for both 4 ohm resistors as both have the same current going into and out of the junctions near them. We can then use this to determine the voltage drop across each of the resistors.
Now let’s add this to our chart.
We can now use Kirchoff’s loop law to determine the voltage across the 10 Ohm resistor. Let’s analyze the loop that goes from the 5, to the 4 to the 10 back through the 4 and then through 3 Ohm resistor.
We can now use Ohm’s Law to determine the current through the 10 Ohm resistor.
Compare your answer with the correct one above
Calculate the current in the 15 Ohm Resistor.
Calculate the current in the 15 Ohm Resistor.
To begin, let us start with the 
resistor and the 
resistor that are in parallel. In parallel we can add resistors through the equation 
This new resistor is now in series with the two 
resistors. In series we can just add these resistors up.
This new resistor is now in parallel with the 
resistor. In parallel we can add resistors through the equation 
This new resistor is now in series with the 
and 
resistor. In series we can just add these resistors up.
Now that we have the equivalent resistance of the circuit. We can now determine the current flowing out of the battery.
Rearrange to solve for current.
One of the best ways to work through a problem like this is to create a V= IR chart for all the components of the circuit.
We know that the current that is flowing out of the battery is the current that is flowing through both by 5 and 3 Ohm resistors since all of these are in series. So we can put this information into our chart.
Using Ohm’s Law we can determine the voltage for each of these two resistors.
We can now use Kirchoff’s loop law through the loop of the 5, 3, and 14 Ohm resistor to determine the voltage that is traveling through the 14 Ohm resistor.
We can now use Ohm’s law and our voltage to determine the current going through the 14 Ohm resistor.
We can now add this information to our chart.
Next we can analyze the current in the Junction between the 5, 14 and 4 Ohm resistors. Kirchoff’s laws state that the sum of the current flowing in and out of the junction must equal 0.
We have 4A flowing in from the 5 Ohm resistor and 1A flowing out to go through the 14 Ohm resistor.
So the current going through the 4 Ohm resistor is 3 amps. This will be the same for both 4 ohm resistors as both have the same current going into and out of the junctions near them. We can then use this to determine the voltage drop across each of the resistors.
Now let’s add this to our chart.
We can now use Kirchoff’s loop law to determine the voltage across the 10 Ohm resistor. Let’s analyze the loop that goes from the 5, to the 4 to the 10 back through the 4 and then through 3 Ohm resistor.
We can now use Ohm’s Law to determine the current through the 10 Ohm resistor.
We can now add this information to our chart.
We can now analyze the junction between the 4, 10 and 15 Ohm resistor.
Kirchoff’s laws state that the sum of the current flowing in and out of the junction must equal 0.
We have 2A flowing in from the 4 Ohm resistor and 1.2A flowing out to go through the 10 Ohm resistor.
To begin, let us start with the 
This new resistor is now in series with the two 
This new resistor is now in parallel with the 
This new resistor is now in series with the 
Now that we have the equivalent resistance of the circuit. We can now determine the current flowing out of the battery.
Rearrange to solve for current.
One of the best ways to work through a problem like this is to create a V= IR chart for all the components of the circuit.
We know that the current that is flowing out of the battery is the current that is flowing through both by 5 and 3 Ohm resistors since all of these are in series. So we can put this information into our chart.
Using Ohm’s Law we can determine the voltage for each of these two resistors.
We can now use Kirchoff’s loop law through the loop of the 5, 3, and 14 Ohm resistor to determine the voltage that is traveling through the 14 Ohm resistor.
We can now use Ohm’s law and our voltage to determine the current going through the 14 Ohm resistor.
We can now add this information to our chart.
Next we can analyze the current in the Junction between the 5, 14 and 4 Ohm resistors. Kirchoff’s laws state that the sum of the current flowing in and out of the junction must equal 0.
We have 4A flowing in from the 5 Ohm resistor and 1A flowing out to go through the 14 Ohm resistor.
So the current going through the 4 Ohm resistor is 3 amps. This will be the same for both 4 ohm resistors as both have the same current going into and out of the junctions near them. We can then use this to determine the voltage drop across each of the resistors.
Now let’s add this to our chart.
We can now use Kirchoff’s loop law to determine the voltage across the 10 Ohm resistor. Let’s analyze the loop that goes from the 5, to the 4 to the 10 back through the 4 and then through 3 Ohm resistor.
We can now use Ohm’s Law to determine the current through the 10 Ohm resistor.
We can now add this information to our chart.
We can now analyze the junction between the 4, 10 and 15 Ohm resistor.
Kirchoff’s laws state that the sum of the current flowing in and out of the junction must equal 0.
We have 2A flowing in from the 4 Ohm resistor and 1.2A flowing out to go through the 10 Ohm resistor.
Compare your answer with the correct one above
Calculate the voltage drop from point 
to point 
.
Calculate the voltage drop from point 
To begin we need to simplify the circuit to get the equivalent resistance. Let’s start with the 3 and 6 Ohm resistors in parallel.
Now we can add this resistor to the 4 Ohm resistor as they are in series.
We can now determine the current coming out of the battery using Ohm’s Law.
Rearrange to solve for current.
The current coming out of the battery will be the same current that moves through the 4 Ohm resistor. So we can determine the voltage drop across the 4 ohm resistor.
We can then use Kirchoff’s loop law to determine the voltage drop from point 
to point 
.
Let’s analyze the loop that goes from the battery to the 4 ohm resistor and through the 3 ohm resistor.
To begin we need to simplify the circuit to get the equivalent resistance. Let’s start with the 3 and 6 Ohm resistors in parallel.
Now we can add this resistor to the 4 Ohm resistor as they are in series.
We can now determine the current coming out of the battery using Ohm’s Law.
Rearrange to solve for current.
The current coming out of the battery will be the same current that moves through the 4 Ohm resistor. So we can determine the voltage drop across the 4 ohm resistor.
We can then use Kirchoff’s loop law to determine the voltage drop from point 
Let’s analyze the loop that goes from the battery to the 4 ohm resistor and through the 3 ohm resistor.
Compare your answer with the correct one above
Calculate the current through the 6 ohm resistor.
Calculate the current through the 6 ohm resistor.
To begin we need to simplify the circuit to get the equivalent resistance. Let’s start with the 3 and 6 Ohm resistors in parallel.
Now we can add this resistor to the 4 Ohm resistor as they are in series.
We can now determine the current coming out of the battery using Ohm’s Law.
Rearrange to solve for current.
The current coming out of the battery will be the same current that moves through the 4 Ohm resistor. So we can determine the voltage drop across the 4 ohm resistor.
We can then use Kirchoff’s loop law to determine the voltage drop across the 6 Ohm resistor. Let’s analyze the loop that goes from the battery to the 4 ohm resistor and through the 6 ohm resistor.
To begin we need to simplify the circuit to get the equivalent resistance. Let’s start with the 3 and 6 Ohm resistors in parallel.
Now we can add this resistor to the 4 Ohm resistor as they are in series.
We can now determine the current coming out of the battery using Ohm’s Law.
Rearrange to solve for current.
The current coming out of the battery will be the same current that moves through the 4 Ohm resistor. So we can determine the voltage drop across the 4 ohm resistor.
We can then use Kirchoff’s loop law to determine the voltage drop across the 6 Ohm resistor. Let’s analyze the loop that goes from the battery to the 4 ohm resistor and through the 6 ohm resistor.
Compare your answer with the correct one above
Calculate the voltage drop across the 4 ohm resistor.
Calculate the voltage drop across the 4 ohm resistor.
To begin we need to simplify the circuit to get the equivalent resistance. Let’s start with the 3 and 6 Ohm resistors in parallel.
Now we can add this resistor to the 4 Ohm resistor as they are in series.
We can now determine the current coming out of the battery using Ohm’s Law.
Rearrange to solve for current.
The current coming out of the battery will be the same current that moves through the 4 Ohm resistor. So we can determine the voltage drop across the 4 ohm resistor.
To begin we need to simplify the circuit to get the equivalent resistance. Let’s start with the 3 and 6 Ohm resistors in parallel.
Now we can add this resistor to the 4 Ohm resistor as they are in series.
We can now determine the current coming out of the battery using Ohm’s Law.
Rearrange to solve for current.
The current coming out of the battery will be the same current that moves through the 4 Ohm resistor. So we can determine the voltage drop across the 4 ohm resistor.
Compare your answer with the correct one above
Kirchoff’s loop rule is an example of
Kirchoff’s loop rule is an example of
Kirchoff’s loop law states that the sum of the voltage around a loop must equal zero. In other words, the voltage that is being provided by the batteries in the circuit must equal the voltage being used by the objects in the circuit. Voltage is a measure of the potential difference, or energy within the circuit. In other words, the battery does a certain amount of work and provides energy to the circuit which is then used by all the parts of the circuit. Therefore this is an example of conservation of energy.
Kirchoff’s loop law states that the sum of the voltage around a loop must equal zero. In other words, the voltage that is being provided by the batteries in the circuit must equal the voltage being used by the objects in the circuit. Voltage is a measure of the potential difference, or energy within the circuit. In other words, the battery does a certain amount of work and provides energy to the circuit which is then used by all the parts of the circuit. Therefore this is an example of conservation of energy.
Compare your answer with the correct one above
Kirchoff’s junction rule is an example of
Kirchoff’s junction rule is an example of
Kirchoff’s loop rules states the sum of the current going into and out of the junction must equal 0. In other words, the current going in must equal the current going on. Current is a measure of the flow of charge. Therefore, this law is conservation of charge as the number of electrons going into a junction must equal the number of electrons flowing out.
Kirchoff’s loop rules states the sum of the current going into and out of the junction must equal 0. In other words, the current going in must equal the current going on. Current is a measure of the flow of charge. Therefore, this law is conservation of charge as the number of electrons going into a junction must equal the number of electrons flowing out.
Compare your answer with the correct one above
Which of the equations here is valid for the circuit shown?
Which of the equations here is valid for the circuit shown?
To answer this question we must consider Kirchoff’s Loop Law. This law states that the voltage around any loop must equal 0. In this case there are two different loops at play. To begin, let’s start on the left with the 2 Volt battery.
As we start with the 2 Volt battery, we then move into the 1 Ohm resistor with 
going through it. Ohm’s law states that the voltage is equal to the current times the resistance. Therefore the voltage through this circuit is 
Since this resistor is using the voltage this will be a negative voltage when we sum around the loop.
We will continue our loop through the middle of the circuit into the 4 Volt battery. This battery is facing the opposite direction from our 2 Volt battery and therefore will be a negative when it comes to our equation.
Next is the 2 Ohm resistor with 
going through it. According to Ohm’s law the voltage being used by this resistor is equal to 
When summarizing all of these parts we get an equation that looks like 
which simplifies down to 
This is one of the equations available to us and therefore there is no need to analyze any other loops.
To answer this question we must consider Kirchoff’s Loop Law. This law states that the voltage around any loop must equal 0. In this case there are two different loops at play. To begin, let’s start on the left with the 2 Volt battery.
As we start with the 2 Volt battery, we then move into the 1 Ohm resistor with 
We will continue our loop through the middle of the circuit into the 4 Volt battery. This battery is facing the opposite direction from our 2 Volt battery and therefore will be a negative when it comes to our equation.
Next is the 2 Ohm resistor with 
When summarizing all of these parts we get an equation that looks like 
Compare your answer with the correct one above
A closed electric circuit is set up so that there is a resistance of 
and a voltage of 
. What is the current in the circuit?
A closed electric circuit is set up so that there is a resistance of
For this problem, use Ohm's law: 
.
We are given the voltage and the resistance. Using these terms, we can solve for the current.
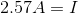
For this problem, use Ohm's law:
We are given the voltage and the resistance. Using these terms, we can solve for the current.
Compare your answer with the correct one above
A current of 
flow in a wire. How many electrons are flowing past any point in the wire per second?
A current of 
The current is a measure of the amount of charge that passes a given point in a certain amount of time.
To determine how many electrons are passing this point we need to look at the charge of 1 electron and do a conversion.
The current is a measure of the amount of charge that passes a given point in a certain amount of time.
To determine how many electrons are passing this point we need to look at the charge of 1 electron and do a conversion.
Compare your answer with the correct one above
What is the maximum power consumption of 
portable CD player that draw a maximum of 
of current?
What is the maximum power consumption of 
The power in a circuit is equal to the current times the voltage.
The power in a circuit is equal to the current times the voltage.
Compare your answer with the correct one above
The direction of conventional current is taken to be the direction that __________________ .
The direction of conventional current is taken to be the direction that __________________ .
We often think of current flowing from the top of the battery to the bottom of the battery. The top of the battery has a higher electrical potential than the bottom of the battery and is associated as being positive. Charges interact in such a way where like charges repel and opposite charges attract. Since we think of the charges traveling away from the positive end of the battery and toward the negative end of the battery, this would model the motion of a positive charge (away from positive and toward negative). Since it is not protons that move through the circuit, but rather electrons. It is more accurate to describe the flow of electrons from the negative side of the battery to the positive side.
We often think of current flowing from the top of the battery to the bottom of the battery. The top of the battery has a higher electrical potential than the bottom of the battery and is associated as being positive. Charges interact in such a way where like charges repel and opposite charges attract. Since we think of the charges traveling away from the positive end of the battery and toward the negative end of the battery, this would model the motion of a positive charge (away from positive and toward negative). Since it is not protons that move through the circuit, but rather electrons. It is more accurate to describe the flow of electrons from the negative side of the battery to the positive side.
Compare your answer with the correct one above
The total amount of charge that passes through a wire’s full cross section at any point per unit of time is referred to as
The total amount of charge that passes through a wire’s full cross section at any point per unit of time is referred to as
Current is defined as the amount of charge that passes through a specific area of a wire in a specific interval of time. It is measured in Amps which are Coulombs per second.
Current is defined as the amount of charge that passes through a specific area of a wire in a specific interval of time. It is measured in Amps which are Coulombs per second.
Compare your answer with the correct one above
If the resistance in a constant voltage circuit is doubled, the power dissipated by that circuit
If the resistance in a constant voltage circuit is doubled, the power dissipated by that circuit
Decrease to one half its original value
The equation for Power is
According to Ohm’s Law
We can rearrange this equation for current as this is what is changing in our circuit.
We can then substitute this back into the power equation.
If we have the original value
and our second value 
We can rearrange both for the voltage and set them equal to each other
, 
We know that 
So we can substitute this value in
And solve for 
Therefore the power would be cut in half.
Decrease to one half its original value
The equation for Power is
According to Ohm’s Law
We can rearrange this equation for current as this is what is changing in our circuit.
We can then substitute this back into the power equation.
If we have the original value
We can rearrange both for the voltage and set them equal to each other
We know that
So we can substitute this value in
And solve for
Therefore the power would be cut in half.
Compare your answer with the correct one above
Why might a circuit breaker open if you plug too many electrical devices into a single circuit?
Why might a circuit breaker open if you plug too many electrical devices into a single circuit?
When plugin objects into a single circuit, these objects are connected in parallel as each one will receive the 120V from the electrical outlet. However, as additional objects are added, the current is thereby increased. Circuit breakers are designed to trip once the current reaches a maximum load and shuts down the circuit to protect the wires, and the devices that are plugged into the circuit as high current can damage these devices.
When plugin objects into a single circuit, these objects are connected in parallel as each one will receive the 120V from the electrical outlet. However, as additional objects are added, the current is thereby increased. Circuit breakers are designed to trip once the current reaches a maximum load and shuts down the circuit to protect the wires, and the devices that are plugged into the circuit as high current can damage these devices.
Compare your answer with the correct one above
A 4.5V battery is connected to a bulb whose resistance is 
. How many electrons leave the battery per minute?
A 4.5V battery is connected to a bulb whose resistance is 
We first need to determine the current coming through the bulb. We can use Ohm’s law to determine this.
Current by definition is the amount of charge per unit time.
We are looking at the number of electrons in one minute which is 60 seconds.
We now know the amount of charge passing through in 60 seconds. We know that the charge of the electron is 
. We can use this to figure out how many electrons are going through.
We first need to determine the current coming through the bulb. We can use Ohm’s law to determine this.
Current by definition is the amount of charge per unit time.
We are looking at the number of electrons in one minute which is 60 seconds.
We now know the amount of charge passing through in 60 seconds. We know that the charge of the electron is 
Compare your answer with the correct one above
Nothing happens when birds land on a power line, yet we are warned not to touch a power line with a ladder. What is the difference?
Nothing happens when birds land on a power line, yet we are warned not to touch a power line with a ladder. What is the difference?
Electricity travels from the point of highest potential to the lowest potential. We measure the difference between these two potentials as the voltage. Since both of the birds' feet are on the wire, both feet have the same potential. However, if the ladder touches the power line and the bottom of the ladder is on the ground, there is a much higher potential difference (as the ground is at 0 potential). Therefore the electricity will travel down the ladder!
Electricity travels from the point of highest potential to the lowest potential. We measure the difference between these two potentials as the voltage. Since both of the birds' feet are on the wire, both feet have the same potential. However, if the ladder touches the power line and the bottom of the ladder is on the ground, there is a much higher potential difference (as the ground is at 0 potential). Therefore the electricity will travel down the ladder!
Compare your answer with the correct one above
When a light switch is turned on, the light comes on immediately because
When a light switch is turned on, the light comes on immediately because
It's kind of like when you turn on the faucet; the water doesn't have to travel from the water tower to your house before it starts flowing. Similarly, the electrons are always in the circuit. Once the switch is turned on, there is a voltage difference present, which is what then pushes these electrons through the circuit (like turning on the faucet).
It's kind of like when you turn on the faucet; the water doesn't have to travel from the water tower to your house before it starts flowing. Similarly, the electrons are always in the circuit. Once the switch is turned on, there is a voltage difference present, which is what then pushes these electrons through the circuit (like turning on the faucet).
Compare your answer with the correct one above