Calculating Momentum - High School Physics
Card 0 of 20
A  crate slides along the floor for
crate slides along the floor for  before stopping. If it was initially moving with a velocity of
before stopping. If it was initially moving with a velocity of  , what is the force of friction?
, what is the force of friction?
A 


The fastest way to solve a problem like this is with momentum.
Remember that momentum is equal to mass times velocity:  . We can rewrite this equation in terms of force.
. We can rewrite this equation in terms of force.


Using this transformation, we can see that momentum is also equal to force times time.
 can also be thought of as
can also be thought of as  .
.
Expand this equation to include our given values.

Since the crate is not moving at the end, its final velocity is zero. Plug in the given values and solve for the force.





The fastest way to solve a problem like this is with momentum.
Remember that momentum is equal to mass times velocity: 
Using this transformation, we can see that momentum is also equal to force times time.


Expand this equation to include our given values.
Since the crate is not moving at the end, its final velocity is zero. Plug in the given values and solve for the force.
Compare your answer with the correct one above
A  crate slides along the floor for
crate slides along the floor for  before stopping. If it was initially moving with a velocity of
before stopping. If it was initially moving with a velocity of  , what is the force of friction?
, what is the force of friction?
A 


The fastest way to solve a problem like this is with momentum.
Remember that momentum is equal to mass times velocity:  . We can rewrite this equation in terms of force.
. We can rewrite this equation in terms of force.


Using this transformation, we can see that momentum is also equal to force times time.
 can also be thought of as
can also be thought of as  .
.
Expand this equation to include our given values.

Since the object is not moving at the end, its final velocity is zero. Plug in the given values and solve for the force.





We would expect the answer to be negative because the force of friction acts in the direction opposite to the initial velocity.
The fastest way to solve a problem like this is with momentum.
Remember that momentum is equal to mass times velocity: 
Using this transformation, we can see that momentum is also equal to force times time.


Expand this equation to include our given values.
Since the object is not moving at the end, its final velocity is zero. Plug in the given values and solve for the force.
We would expect the answer to be negative because the force of friction acts in the direction opposite to the initial velocity.
Compare your answer with the correct one above
A  crate slides along a floor with a starting velocity of
crate slides along a floor with a starting velocity of  . If the force due to friction is
. If the force due to friction is  , how long will it take before stopping?
, how long will it take before stopping?
A 


The fastest way to solve a problem like this is with momentum.
Remember that momentum is equal to mass times velocity:  . We can rewrite this equation in terms of force.
. We can rewrite this equation in terms of force.


Using this transformation, we can see that momentum is also equal to force times time.
 can also be thought of as
can also be thought of as  .
.
Expand this equation to include our given values.

Since the crate is not moving at the end, its final velocity is zero. Plug in the given values and solve for the time that it is in motion.





The fastest way to solve a problem like this is with momentum.
Remember that momentum is equal to mass times velocity: 
Using this transformation, we can see that momentum is also equal to force times time.


Expand this equation to include our given values.
Since the crate is not moving at the end, its final velocity is zero. Plug in the given values and solve for the time that it is in motion.
Compare your answer with the correct one above
A  ball hits a brick wall with a velocity of
ball hits a brick wall with a velocity of  and bounces back at the same speed. If the ball is in contact with the wall for
and bounces back at the same speed. If the ball is in contact with the wall for  , what is the force exerted by the wall on the ball?
, what is the force exerted by the wall on the ball?
A 


The fastest way to solve a problem like this is with momentum.
Remember that momentum is equal to mass times velocity:  . We can rewrite this equation in terms of force.
. We can rewrite this equation in terms of force.


Using this transformation, we can see that momentum is also equal to force times time.
 can also be thought of as
can also be thought of as  .
.
Expand this equation to include our given values.

Even though the ball is bouncing back at the same "speed", its velocity will now be negative as it is moving in the opposite direction. Using these given values, we can solve for the force that acts on the ball.





Our answer is negative because the force is moving the ball in the OPPOSITE direction from the way it was originally heading.
The fastest way to solve a problem like this is with momentum.
Remember that momentum is equal to mass times velocity: 
Using this transformation, we can see that momentum is also equal to force times time.


Expand this equation to include our given values.
Even though the ball is bouncing back at the same "speed", its velocity will now be negative as it is moving in the opposite direction. Using these given values, we can solve for the force that acts on the ball.
Our answer is negative because the force is moving the ball in the OPPOSITE direction from the way it was originally heading.
Compare your answer with the correct one above
A  ball moving at
ball moving at  strikes a piece of paper. It breaks through the paper and continues moving in the same direction. If the paper exerted a force of
strikes a piece of paper. It breaks through the paper and continues moving in the same direction. If the paper exerted a force of  on the ball and the two are in contact for
on the ball and the two are in contact for  , what is the final momentum of the ball?
, what is the final momentum of the ball?
A 



Remember that momentum is equal to mass times velocity:  . We can rewrite this equation in terms of force.
. We can rewrite this equation in terms of force.


Using this transformation, we can see that momentum is also equal to force times time.
 can also be thought of as
can also be thought of as  .
.
Expand this equation to include our given values.

We are given the mass and initial velocity, allowing us to solve for the initial momentum, and the force and time, allowing us to evaluate the right side of the equation. Using these values we can solve for the final momentum of the ball.




Remember that momentum is equal to mass times velocity: 
Using this transformation, we can see that momentum is also equal to force times time.


Expand this equation to include our given values.
We are given the mass and initial velocity, allowing us to solve for the initial momentum, and the force and time, allowing us to evaluate the right side of the equation. Using these values we can solve for the final momentum of the ball.
Compare your answer with the correct one above
Susan pushes a  car with
car with  of force on a frictionless surface. How long does she need to push the car to get it to a velocity of
of force on a frictionless surface. How long does she need to push the car to get it to a velocity of  if it starts at rest?
if it starts at rest?
Susan pushes a 


The fastest way to solve a problem like this is with momentum.
Remember that momentum is equal to mass times velocity:  . We can rewrite this equation in terms of force.
. We can rewrite this equation in terms of force.


Using this transformation, we can see that momentum is also equal to force times time.
 can also be thought of as
can also be thought of as  .
.
Expand this equation to include our given values.

Since the car is not moving at the beginning, its initial velocity is zero. Plug in the given values and solve for the time required to change the velocity to the given value.




The fastest way to solve a problem like this is with momentum.
Remember that momentum is equal to mass times velocity: 
Using this transformation, we can see that momentum is also equal to force times time.


Expand this equation to include our given values.
Since the car is not moving at the beginning, its initial velocity is zero. Plug in the given values and solve for the time required to change the velocity to the given value.
Compare your answer with the correct one above
A  hammer moving with a velocity of
hammer moving with a velocity of  strikes a nail. The two are in contact for
strikes a nail. The two are in contact for  , after which the hammer has a velocity of
, after which the hammer has a velocity of  . What is the force of the hammer on the nail?
. What is the force of the hammer on the nail?
A 



The fastest way to solve a problem like this is with momentum.
Remember that momentum is equal to mass times velocity:  . We can rewrite this equation in terms of force.
. We can rewrite this equation in terms of force.


Using this transformation, we can see that momentum is also equal to force times time.
 can also be thought of as
can also be thought of as  .
.
Expand this equation to include our given values.

Since the hammer is not moving at the end, its final velocity is zero. Plug in the given values and solve for the force.





This equation solves for the force of the nail on the hammer, as we were looking purely at the momentum of the hammer.
According to Newton's third law,  . This means that if the nail exerts
. This means that if the nail exerts  of force on the hammer, then the hammer must exert
of force on the hammer, then the hammer must exert  of force on the nail.
of force on the nail.
The fastest way to solve a problem like this is with momentum.
Remember that momentum is equal to mass times velocity: 
Using this transformation, we can see that momentum is also equal to force times time.


Expand this equation to include our given values.
Since the hammer is not moving at the end, its final velocity is zero. Plug in the given values and solve for the force.
This equation solves for the force of the nail on the hammer, as we were looking purely at the momentum of the hammer.
According to Newton's third law, 


Compare your answer with the correct one above
A  hammer moving with a velocity of
hammer moving with a velocity of  strikes a nail, after which the hammer has a velocity of
strikes a nail, after which the hammer has a velocity of  . If the hammer strikes the nail with
. If the hammer strikes the nail with  of force, how long were the two in contact?
of force, how long were the two in contact?
A 



The fastest way to solve a problem like this is with momentum.
Remember that momentum is equal to mass times velocity:  . We can rewrite this equation in terms of force.
. We can rewrite this equation in terms of force.


Using this transformation, we can see that momentum is also equal to force times time.
 can also be thought of as
can also be thought of as  .
.
Expand this equation to include our given values.

Since the hammer is not moving at the end, its final velocity is zero. This allows us to set up the left side of our equation.

The problem gave us the force of the hammer on the nail, but not the force of the nail on the hammer, which is what we need for our equation since we are looking purely at the momentum of the hammer.
Fortunately, Newton's third law can help us. It states that  . This means that if the hammer exerts
. This means that if the hammer exerts  of force on the nail, then the nail must exert
of force on the nail, then the nail must exert  of force on the hammer.
of force on the hammer.
We can plug that value in for force and solve our equation for time.





The fastest way to solve a problem like this is with momentum.
Remember that momentum is equal to mass times velocity: 
Using this transformation, we can see that momentum is also equal to force times time.


Expand this equation to include our given values.
Since the hammer is not moving at the end, its final velocity is zero. This allows us to set up the left side of our equation.
The problem gave us the force of the hammer on the nail, but not the force of the nail on the hammer, which is what we need for our equation since we are looking purely at the momentum of the hammer.
Fortunately, Newton's third law can help us. It states that 


We can plug that value in for force and solve our equation for time.
Compare your answer with the correct one above
A  ball hits a brick wall with a velocity of
ball hits a brick wall with a velocity of 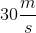 and bounces back at the same speed. If the ball is in contact with the wall for
and bounces back at the same speed. If the ball is in contact with the wall for  , what is the value of the force exerted by the wall on the ball?
, what is the value of the force exerted by the wall on the ball?
A 

The fastest way to solve a problem like this is with momentum.
Remember that momentum is equal to mass times velocity: 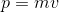 . We can rewrite this equation in terms of force.
. We can rewrite this equation in terms of force.

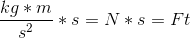
Using this transformation, we can see that momentum is also equal to force times time.
 can also be thought of as
can also be thought of as  .
.
Expand this equation to include our given values.
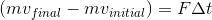
Even though the ball is bouncing back at the same "speed" its velocity will now be negative, as it is moving in the opposite direction. Using this understanding we can solve for the force in our equation.




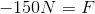
Our answer is negative because the force is moving the ball in the OPPOSITE direction from the way it was originally heading.
The fastest way to solve a problem like this is with momentum.
Remember that momentum is equal to mass times velocity: 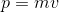
Using this transformation, we can see that momentum is also equal to force times time.


Expand this equation to include our given values.
Even though the ball is bouncing back at the same "speed" its velocity will now be negative, as it is moving in the opposite direction. Using this understanding we can solve for the force in our equation.
Our answer is negative because the force is moving the ball in the OPPOSITE direction from the way it was originally heading.
Compare your answer with the correct one above
A  hammer moving with a velocity of
hammer moving with a velocity of  strikes a nail. The two are in contact for
strikes a nail. The two are in contact for  , after which the hammer has a velocity of
, after which the hammer has a velocity of  . With how much force did the hammer strike the nail?
. With how much force did the hammer strike the nail?
A 



The fastest way to solve a problem like this is with momentum.
Remember that momentum is equal to mass times velocity:  . We can rewrite this equation in terms of force.
. We can rewrite this equation in terms of force.


Using this transformation, we can see that momentum is also equal to force times time.
 can also be thought of as
can also be thought of as  .
.
Expand this equation to include our given values.

Since the hammer is not moving at the end, its final velocity is zero. Plug in the given values and solve for the force.





This equation solves for the force of the nail on the hammer, as we were looking purely at the momentum of the hammer.
According to Newton's third law,  . This means that if the nail exerts
. This means that if the nail exerts  of force on the hammer, then the hammer must exert
of force on the hammer, then the hammer must exert  of force on the nail.
of force on the nail.
Our answer will be  .
.
The fastest way to solve a problem like this is with momentum.
Remember that momentum is equal to mass times velocity: 
Using this transformation, we can see that momentum is also equal to force times time.


Expand this equation to include our given values.
Since the hammer is not moving at the end, its final velocity is zero. Plug in the given values and solve for the force.
This equation solves for the force of the nail on the hammer, as we were looking purely at the momentum of the hammer.
According to Newton's third law, 


Our answer will be 
Compare your answer with the correct one above
A  crate slides along a floor with a starting velocity of
crate slides along a floor with a starting velocity of  . If the force due to friction is
. If the force due to friction is  , how long will it take for the box to come to rest?
, how long will it take for the box to come to rest?
A 


The fastest way to solve a problem like this is with momentum.
Remember that momentum is equal to mass times velocity:  . We can rewrite this equation in terms of force.
. We can rewrite this equation in terms of force.


Using this transformation, we can see that momentum is also equal to force times time.
 can also be thought of as
can also be thought of as  .
.
Expand this equation to include our given values.

Since the box is not moving at the end, its final velocity is zero. Plug in the given values and solve for the time.





The fastest way to solve a problem like this is with momentum.
Remember that momentum is equal to mass times velocity: 
Using this transformation, we can see that momentum is also equal to force times time.


Expand this equation to include our given values.
Since the box is not moving at the end, its final velocity is zero. Plug in the given values and solve for the time.
Compare your answer with the correct one above
A  ball strikes a piece of paper moving at
ball strikes a piece of paper moving at  . It breaks through the paper and continues on in the same direction. If the paper exerted a force of
. It breaks through the paper and continues on in the same direction. If the paper exerted a force of  on the ball and the two are in contact for
on the ball and the two are in contact for  , what is the final momentum of the ball?
, what is the final momentum of the ball?
A 



The fastest way to solve a problem like this is with momentum.
Remember that momentum is equal to mass times velocity:  . We can rewrite this equation in terms of force.
. We can rewrite this equation in terms of force.


Using this transformation, we can see that momentum is also equal to force times time.
 can also be thought of as
can also be thought of as  .
.
Since we're looking for  , we're going to leave that part alone in the problem, but we can expand the rest.
, we're going to leave that part alone in the problem, but we can expand the rest.

From here, plug in the given values and solve for the final momentum.


At this point, remember that  , so sides are now working in the same units.
, so sides are now working in the same units.


The fastest way to solve a problem like this is with momentum.
Remember that momentum is equal to mass times velocity: 
Using this transformation, we can see that momentum is also equal to force times time.


Since we're looking for 
From here, plug in the given values and solve for the final momentum.
At this point, remember that 
Compare your answer with the correct one above
An  car strikes a
car strikes a  car from behind. The bumpers lock and they move forward together. If their new final velocity is equal to
car from behind. The bumpers lock and they move forward together. If their new final velocity is equal to  , what was the initial velocity of the first car?
, what was the initial velocity of the first car?
An 


This is an example of an inelastic collision, as the two cars stick together after colliding. We can assume momentum is conserved.
To make the equation easier, let's call the first car "1" and the second car "2."
Using conservation of momentum and the equation for momentum,  , we can set up the following equation.
, we can set up the following equation.

Since the cars stick together, they will have the same final velocity. We know the second car starts at rest, and the velocity of the first car is given. Plug in these values and solve for the initial velocity of the first car.





This is an example of an inelastic collision, as the two cars stick together after colliding. We can assume momentum is conserved.
To make the equation easier, let's call the first car "1" and the second car "2."
Using conservation of momentum and the equation for momentum, 
Since the cars stick together, they will have the same final velocity. We know the second car starts at rest, and the velocity of the first car is given. Plug in these values and solve for the initial velocity of the first car.
Compare your answer with the correct one above
Susan pushes a car  with
with  of force. How long does she need to push it to get it to a velocity of
of force. How long does she need to push it to get it to a velocity of  if it starts at rest and there is no friction?
if it starts at rest and there is no friction?
Susan pushes a car 


The fastest way to solve a problem like this is with momentum.
Remember that momentum is equal to mass times velocity:  . We can rewrite this equation in terms of force.
. We can rewrite this equation in terms of force.


Using this transformation, we can see that momentum is also equal to force times time.
 can also be thought of as
can also be thought of as  .
.
Expand this equation to include our given values.

Since the car starts from rest, its initial velocity is zero. Plug in the given values and solve for the time.




The fastest way to solve a problem like this is with momentum.
Remember that momentum is equal to mass times velocity: 
Using this transformation, we can see that momentum is also equal to force times time.


Expand this equation to include our given values.
Since the car starts from rest, its initial velocity is zero. Plug in the given values and solve for the time.
Compare your answer with the correct one above
A  hammer moving with a velocity of
hammer moving with a velocity of  strikes a nail, after which the hammer has a velocity of
strikes a nail, after which the hammer has a velocity of  . If the hammer strikes the nail with
. If the hammer strikes the nail with  of force, how long were the two in contact?
of force, how long were the two in contact?
A 



The fastest way to solve a problem like this is with momentum.
Remember that momentum is equal to mass times velocity:  . We can rewrite this equation in terms of force.
. We can rewrite this equation in terms of force.


Using this transformation, we can see that momentum is also equal to force times time.
 can also be thought of as
can also be thought of as  .
.
Expand this equation to include our given values.

Since the hammer is not moving at the end, its final velocity is zero.

The problem gave us the force of the hammer on the nail, but not the force of the nail on the hammer, which is what we need for the equation as we are looking purely at the momentum of the hammer. Fortunately, Newton's third law can help us. It states that  . This means that if the hammer exerts
. This means that if the hammer exerts  of force on the nail, then the nail must exert
of force on the nail, then the nail must exert  of force on the hammer.
of force on the hammer.
We can plug that value in for the force and solve for the time.





The fastest way to solve a problem like this is with momentum.
Remember that momentum is equal to mass times velocity: 
Using this transformation, we can see that momentum is also equal to force times time.


Expand this equation to include our given values.
Since the hammer is not moving at the end, its final velocity is zero.
The problem gave us the force of the hammer on the nail, but not the force of the nail on the hammer, which is what we need for the equation as we are looking purely at the momentum of the hammer. Fortunately, Newton's third law can help us. It states that 


We can plug that value in for the force and solve for the time.
Compare your answer with the correct one above
A  hammer moving with a velocity of
hammer moving with a velocity of  strikes a nail, after which the hammer has a velocity of
strikes a nail, after which the hammer has a velocity of  . If the hammer strikes the nail with
. If the hammer strikes the nail with  of force, how long were the two in contact?
of force, how long were the two in contact?
A 



The fastest way to solve a problem like this is with momentum.
Remember that momentum is equal to mass times velocity:  . We can rewrite this equation in terms of force.
. We can rewrite this equation in terms of force.


Using this transformation, we can see that momentum is also equal to force times time.
 can also be thought of as
can also be thought of as  .
.
Expand this equation to include our given values.

Since the hammer is not moving at the end, its final velocity is zero.

The problem gave us the force of the hammer on the nail, but not the force of the nail on the hammer, which is what we need as we are looking purely at the momentum of the hammer.
Fortunately, Newton's third law can help us. It states that  . This means that if the hammer exerts
. This means that if the hammer exerts  of force on the nail, then the nail must exert
of force on the nail, then the nail must exert  of force on the hammer.
of force on the hammer.
We can plug that value in for the force and solve.





The fastest way to solve a problem like this is with momentum.
Remember that momentum is equal to mass times velocity: 
Using this transformation, we can see that momentum is also equal to force times time.


Expand this equation to include our given values.
Since the hammer is not moving at the end, its final velocity is zero.
The problem gave us the force of the hammer on the nail, but not the force of the nail on the hammer, which is what we need as we are looking purely at the momentum of the hammer.
Fortunately, Newton's third law can help us. It states that 


We can plug that value in for the force and solve.
Compare your answer with the correct one above
A  crate slides along the floor for
crate slides along the floor for  before stopping. If it was initially moving with a velocity of
before stopping. If it was initially moving with a velocity of  , what is the force of friction?
, what is the force of friction?
A 


The fastest way to solve a problem like this is with momentum.
Remember that momentum is equal to mass times velocity:  . We can rewrite this equation in terms of force.
. We can rewrite this equation in terms of force.


Using this transformation, we can see that momentum is also equal to force times time.
 can also be thought of as
can also be thought of as  .
.
Expand this equation to include our given values.

Since the crate is not moving at the end, its final velocity is zero. Plug in the given values and solve for the force.





The fastest way to solve a problem like this is with momentum.
Remember that momentum is equal to mass times velocity: 
Using this transformation, we can see that momentum is also equal to force times time.


Expand this equation to include our given values.
Since the crate is not moving at the end, its final velocity is zero. Plug in the given values and solve for the force.
Compare your answer with the correct one above
A  hammer moving with a velocity of
hammer moving with a velocity of  strikes a nail. The two are in contact for
strikes a nail. The two are in contact for  , after which the hammer has a velocity of
, after which the hammer has a velocity of  . How much force went into the nail?
. How much force went into the nail?
A 



The fastest way to solve a problem like this is with momentum.
Remember that momentum is equal to mass times velocity:  . We can rewrite this equation in terms of force.
. We can rewrite this equation in terms of force.


Using this transformation, we can see that momentum is also equal to force times time.
 can also be thought of as
can also be thought of as  .
.
Expand this equation to include our given values.

Since the hammer is not moving at the end, its final velocity is zero. Plug in the given values and solve for the force.





This equation solves for the force of the nail on the hammer, as we were looking purely at the momentum of the hammer; however, we need to find the force of the hammer on the nail. Newton's third law states that  .
.
This means that if the nail exerts  of force on the hammer, then the hammer must exert
of force on the hammer, then the hammer must exert  of force on the nail; therefore, our answer will be
of force on the nail; therefore, our answer will be  .
.
The fastest way to solve a problem like this is with momentum.
Remember that momentum is equal to mass times velocity: 
Using this transformation, we can see that momentum is also equal to force times time.


Expand this equation to include our given values.
Since the hammer is not moving at the end, its final velocity is zero. Plug in the given values and solve for the force.
This equation solves for the force of the nail on the hammer, as we were looking purely at the momentum of the hammer; however, we need to find the force of the hammer on the nail. Newton's third law states that 
This means that if the nail exerts 


Compare your answer with the correct one above
A  crate slides along a floor with a starting velocity of
crate slides along a floor with a starting velocity of  . If the force due to friction is
. If the force due to friction is  , how long will it take before the crate slides to a stop?
, how long will it take before the crate slides to a stop?
A 


The fastest way to solve a problem like this is with momentum.
Remember that momentum is equal to mass times velocity:  . We can rewrite this equation in terms of force.
. We can rewrite this equation in terms of force.


Using this transformation, we can see that momentum is also equal to force times time.
 can also be thought of as
can also be thought of as  .
.
Expand this equation to include our given values.

Since the crate is not moving at the end, its final velocity is zero. Plug in the given values and solve for the time.





The fastest way to solve a problem like this is with momentum.
Remember that momentum is equal to mass times velocity: 
Using this transformation, we can see that momentum is also equal to force times time.


Expand this equation to include our given values.
Since the crate is not moving at the end, its final velocity is zero. Plug in the given values and solve for the time.
Compare your answer with the correct one above
Courtney pushes a car  with
with  of force along a frictionless surface. If the car is initially at rest, how long does she need to push for the car to reach a velocity of
of force along a frictionless surface. If the car is initially at rest, how long does she need to push for the car to reach a velocity of  ?
?
Courtney pushes a car 


The fastest way to solve a problem like this is with momentum.
Remember that momentum is equal to mass times velocity:  . We can rewrite this equation in terms of force.
. We can rewrite this equation in terms of force.


Using this transformation, we can see that momentum is also equal to force times time.
 can also be thought of as
can also be thought of as  .
.
Expand this equation to include our given values.

Since the car is not moving at the beginning, its initial velocity is zero. Plug in the given values and solve for the time.




The fastest way to solve a problem like this is with momentum.
Remember that momentum is equal to mass times velocity: 
Using this transformation, we can see that momentum is also equal to force times time.


Expand this equation to include our given values.
Since the car is not moving at the beginning, its initial velocity is zero. Plug in the given values and solve for the time.
Compare your answer with the correct one above