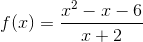Understanding the Definition of Limits - High School Math
Card 0 of 1
A limit describes what 
-value a function approaches as 
approaches a certain value (in this case,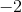 
). The easiest way to find what 
-value a function approaches is to substitute the 
-value into the equation.
Substituting 
for 
gives us an undefined value (which is NOT the same thing as 0). This means the function is not defined at that point. However, just because a function is undefined at a point doesn't mean it doesn't have a limit. The limit is simply whichever value the function is getting close to.
One method of finding the limit is to try and simplify the equation as much as possible:
As you can see, there are common factors between the numerator and the denominator that can be canceled out. (Remember, when you cancel out a factor from a rational equation, it means that the function has a hole -- an undefined point -- where that factor equals zero.)
After canceling out the common factors, we're left with:
Even though the domain of the original function is restricted (
cannot equal 
), we can still substitute into this simplified equation to find the limit at 
A limit describes what
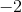
Substituting
One method of finding the limit is to try and simplify the equation as much as possible:
As you can see, there are common factors between the numerator and the denominator that can be canceled out. (Remember, when you cancel out a factor from a rational equation, it means that the function has a hole -- an undefined point -- where that factor equals zero.)
After canceling out the common factors, we're left with:
Even though the domain of the original function is restricted (
Compare your answer with the correct one above