Angles - High School Math
Card 0 of 15
Which one of these is positive in quadrant III?
Which one of these is positive in quadrant III?
The pattern for positive functions is All Student Take Calculus. In quandrant I, all trigonometric functions are positive. In quadrant II, sine is positive. In qudrant III, tangent is positive. In quadrant IV, cosine is positive.
The pattern for positive functions is All Student Take Calculus. In quandrant I, all trigonometric functions are positive. In quadrant II, sine is positive. In qudrant III, tangent is positive. In quadrant IV, cosine is positive.
Compare your answer with the correct one above
Are  and
and  supplementary angles?
supplementary angles?
Are 

Since supplementary angles must add up to  , the given angles are indeed supplementary.
, the given angles are indeed supplementary.
Since supplementary angles must add up to 
Compare your answer with the correct one above
Are  and
and  complementary angles?
complementary angles?
Are 

Complementary angles add up to  . Therefore, these angles are complementary.
. Therefore, these angles are complementary.
Complementary angles add up to 
Compare your answer with the correct one above
Which of the following angles is supplementary to  ?
?
Which of the following angles is supplementary to 
When two angles are supplementary, they add up to  .
.
For this problem, we can set up an equation and solve for the supplementary angle:



When two angles are supplementary, they add up to 
For this problem, we can set up an equation and solve for the supplementary angle:
Compare your answer with the correct one above
What angle is complementary to  ?
?
What angle is complementary to 
Two complementary angles add up to  .
.
Therefore,  .
.


Two complementary angles add up to 
Therefore, 
Compare your answer with the correct one above
What angle is supplementary to  ?
?
What angle is supplementary to 
Supplementary angles add up to  . That means:
. That means:



Supplementary angles add up to 
Compare your answer with the correct one above
Which of the following angles is complementary to  ?
?
Which of the following angles is complementary to 
Two complementary angles add up to  .
.



Two complementary angles add up to 
Compare your answer with the correct one above
What angle is supplementary to  ?
?
What angle is supplementary to 
When two angles are supplementary, they add up to  .
.

Solve for  :
:



When two angles are supplementary, they add up to 
Solve for 
Compare your answer with the correct one above
Find a coterminal angle for  .
.
Find a coterminal angle for 
Coterminal angles are angles that, when drawn in the standard position, share a terminal side. You can find these angles by adding or subtracting 360 to the given angle. Thus, the only angle measurement that works from the answers given is  .
.
Coterminal angles are angles that, when drawn in the standard position, share a terminal side. You can find these angles by adding or subtracting 360 to the given angle. Thus, the only angle measurement that works from the answers given is 
Compare your answer with the correct one above
Which of the following angles is coterminal with  ?
?
Which of the following angles is coterminal with 
For an angle to be coterminal with  , that angle must be of the form
, that angle must be of the form  for some integer
for some integer  - or, equivalently, the difference of the angle measures multiplied by
- or, equivalently, the difference of the angle measures multiplied by  must be an integer. We apply this test to all five choices.
must be an integer. We apply this test to all five choices.
 :
:


 :
:


 :
:
![\left ( \frac{1}{2\pi } \right ) \left [\frac{2\pi}{7} -\left ( -\frac{2\pi}{7} \right ) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/99513/gif.latex)


 :
:
![\left ( \frac{1}{2\pi } \right ) \left [\frac{2\pi}{7} -\left ( -\frac{9\pi}{7} \right ) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/99515/gif.latex)


 :
:
![\left ( \frac{1}{2\pi } \right ) \left [\frac{2\pi}{7} -\left ( -\frac{12\pi}{7} \right ) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/99517/gif.latex)


 is the correct choice, since only that choice passes our test.
is the correct choice, since only that choice passes our test.
For an angle to be coterminal with 









Compare your answer with the correct one above
Which of the following angles is coterminal with  ?
?
Which of the following angles is coterminal with 
For an angle to be coterminal with  , that angle must be of the form
, that angle must be of the form  for some integer
for some integer  - or, equivalently, the difference of the angle measures multiplied by
- or, equivalently, the difference of the angle measures multiplied by  must be an integer. We apply this test to all four choices.
must be an integer. We apply this test to all four choices.
 :
:


 :
:


 :
:


 :
:


All four choices pass the test, so all four angles are coterminal with  .
.
For an angle to be coterminal with 







All four choices pass the test, so all four angles are coterminal with 
Compare your answer with the correct one above
Which of the following choices represents a pair of coterminal angles?
Which of the following choices represents a pair of coterminal angles?
For two angles to be coterminal, they must differ by  for some integer
for some integer  - or, equivalently, the difference of the angle measures multiplied by
- or, equivalently, the difference of the angle measures multiplied by  must be an integer. We apply this test to all five choices.
must be an integer. We apply this test to all five choices.
 :
:

 :
:

 :
:

 :
:

 :
:

The only angles that pass the test - and are therefore coterminal - are  .
.
For two angles to be coterminal, they must differ by 







The only angles that pass the test - and are therefore coterminal - are 
Compare your answer with the correct one above

 .
.


Compare your answer with the correct one above
 and
and  .
.
 all reside along one line, therefore, their sum must be
all reside along one line, therefore, their sum must be 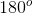 .
.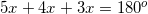


 and
and 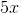 are opposite angles, they must be equal.
are opposite angles, they must be equal.



 .
.
 .
.





