Acute / Obtuse Triangles - High School Math
Card 0 of 20
In the triangle below, AB=BC (figure is not to scale) . If angle A is 41°, what is the measure of angle B?
A (Angle A = 41°)

B C
In the triangle below, AB=BC (figure is not to scale) . If angle A is 41°, what is the measure of angle B?
A (Angle A = 41°)

B C
If angle A is 41°, then angle C must also be 41°, since AB=BC. So, the sum of these 2 angles is:
41° + 41° = 82°
Since the sum of the angles in a triangle is 180°, you can find out the measure of the remaining angle by subtracting 82 from 180:
180° - 82° = 98°
If angle A is 41°, then angle C must also be 41°, since AB=BC. So, the sum of these 2 angles is:
41° + 41° = 82°
Since the sum of the angles in a triangle is 180°, you can find out the measure of the remaining angle by subtracting 82 from 180:
180° - 82° = 98°
Compare your answer with the correct one above
If the average of the measures of two angles in a triangle is 75o, what is the measure of the third angle in this triangle?
If the average of the measures of two angles in a triangle is 75o, what is the measure of the third angle in this triangle?
The sum of the angles in a triangle is 180o: a + b + c = 180
In this case, the average of a and b is 75:
(a + b)/2 = 75, then multiply both sides by 2
(a + b) = 150, then substitute into first equation
150 + c = 180
c = 30
The sum of the angles in a triangle is 180o: a + b + c = 180
In this case, the average of a and b is 75:
(a + b)/2 = 75, then multiply both sides by 2
(a + b) = 150, then substitute into first equation
150 + c = 180
c = 30
Compare your answer with the correct one above
Points A, B, C, D are collinear. The measure of ∠ DCE is 130° and of ∠ AEC is 80°. Find the measure of ∠ EAD.

Points A, B, C, D are collinear. The measure of ∠ DCE is 130° and of ∠ AEC is 80°. Find the measure of ∠ EAD.

To solve this question, you need to remember that the sum of the angles in a triangle is 180°. You also need to remember supplementary angles. If you know what ∠ DCE is, you also know what ∠ ECA is. Hence you know two angles of the triangle, 180°-80°-50°= 50°.
To solve this question, you need to remember that the sum of the angles in a triangle is 180°. You also need to remember supplementary angles. If you know what ∠ DCE is, you also know what ∠ ECA is. Hence you know two angles of the triangle, 180°-80°-50°= 50°.
Compare your answer with the correct one above
Which of the following can NOT be the angles of a triangle?
Which of the following can NOT be the angles of a triangle?
In a triangle, there can only be one obtuse angle. Additionally, all the angle measures must add up to 180.
In a triangle, there can only be one obtuse angle. Additionally, all the angle measures must add up to 180.
Compare your answer with the correct one above
Let the measures, in degrees, of the three angles of a triangle be x, y, and z. If y = 2z, and z = 0.5x - 30, then what is the measure, in degrees, of the largest angle in the triangle?
Let the measures, in degrees, of the three angles of a triangle be x, y, and z. If y = 2z, and z = 0.5x - 30, then what is the measure, in degrees, of the largest angle in the triangle?
The measures of the three angles are x, y, and z. Because the sum of the measures of the angles in any triangle must be 180 degrees, we know that x + y + z = 180. We can use this equation, along with the other two equations given, to form this system of equations:
x + y + z = 180
y = 2z
z = 0.5x - 30
If we can solve for both y and x in terms of z, then we can substitute these values into the first equation and create an equation with only one variable.
Because we are told already that y = 2z, we alreay have the value of y in terms of z.
We must solve the equation z = 0.5x - 30 for x in terms of z.
Add thirty to both sides.
z + 30 = 0.5x
Mutliply both sides by 2
2(z + 30) = 2z + 60 = x
x = 2z + 60
Now we have the values of x and y in terms of z. Let's substitute these values for x and y into the equation x + y + z = 180.
(2z + 60) + 2z + z = 180
5z + 60 = 180
5z = 120
z = 24
Because y = 2z, we know that y = 2(24) = 48. We also determined earlier that x = 2z + 60, so x = 2(24) + 60 = 108.
Thus, the measures of the three angles of the triangle are 24, 48, and 108. The question asks for the largest of these measures, which is 108.
The answer is 108.
The measures of the three angles are x, y, and z. Because the sum of the measures of the angles in any triangle must be 180 degrees, we know that x + y + z = 180. We can use this equation, along with the other two equations given, to form this system of equations:
x + y + z = 180
y = 2z
z = 0.5x - 30
If we can solve for both y and x in terms of z, then we can substitute these values into the first equation and create an equation with only one variable.
Because we are told already that y = 2z, we alreay have the value of y in terms of z.
We must solve the equation z = 0.5x - 30 for x in terms of z.
Add thirty to both sides.
z + 30 = 0.5x
Mutliply both sides by 2
2(z + 30) = 2z + 60 = x
x = 2z + 60
Now we have the values of x and y in terms of z. Let's substitute these values for x and y into the equation x + y + z = 180.
(2z + 60) + 2z + z = 180
5z + 60 = 180
5z = 120
z = 24
Because y = 2z, we know that y = 2(24) = 48. We also determined earlier that x = 2z + 60, so x = 2(24) + 60 = 108.
Thus, the measures of the three angles of the triangle are 24, 48, and 108. The question asks for the largest of these measures, which is 108.
The answer is 108.
Compare your answer with the correct one above
Angles x, y, and z make up the interior angles of a scalene triangle. Angle x is three times the size of y and 1/2 the size of z. How big is angle y.
Angles x, y, and z make up the interior angles of a scalene triangle. Angle x is three times the size of y and 1/2 the size of z. How big is angle y.
The answer is 18
We know that the sum of all the angles is 180. Using the rest of the information given we can write the other two equations:
x + y + z = 180
x = 3y
2x = z
We can solve for y and z in the second and third equations and then plug into the first to solve.
x + (1/3)x + 2x = 180
3\[x + (1/3)x + 2x = 180\]
3x + x + 6x = 540
10x = 540
x = 54
y = 18
z = 108
The answer is 18
We know that the sum of all the angles is 180. Using the rest of the information given we can write the other two equations:
x + y + z = 180
x = 3y
2x = z
We can solve for y and z in the second and third equations and then plug into the first to solve.
x + (1/3)x + 2x = 180
3\[x + (1/3)x + 2x = 180\]
3x + x + 6x = 540
10x = 540
x = 54
y = 18
z = 108
Compare your answer with the correct one above
If the average (arithmetic mean) of two noncongruent angles of an isosceles triangle is  , which of the following is the measure of one of the angles of the triangle?
, which of the following is the measure of one of the angles of the triangle?
If the average (arithmetic mean) of two noncongruent angles of an isosceles triangle is 
Since the triangle is isosceles, we know that 2 of the angles (that sum up to 180) must be equal. The question states that the noncongruent angles average 55°, thus providing us with a system of two equations:


Solving for x and y by substitution, we get x = 70° and y = 40° (which average out to 55°).
70 + 70 + 40 equals 180 also checks out.
Since 70° is not an answer choice for us, we know that the 40° must be one of the angles.
Since the triangle is isosceles, we know that 2 of the angles (that sum up to 180) must be equal. The question states that the noncongruent angles average 55°, thus providing us with a system of two equations:
Solving for x and y by substitution, we get x = 70° and y = 40° (which average out to 55°).
70 + 70 + 40 equals 180 also checks out.
Since 70° is not an answer choice for us, we know that the 40° must be one of the angles.
Compare your answer with the correct one above
The measure of  is
is  . Since
. Since  ,
,  , and
, and  are collinear, and the measure of
are collinear, and the measure of  is
is  , we know that the measure of
, we know that the measure of  is
is  .
.
Because the measures of the three angles in a triangle must add up to  , and two of the angles in triangle
, and two of the angles in triangle  are
are  and
and  , the third angle,
, the third angle,  , is
, is  .
.
The measure of 








Because the measures of the three angles in a triangle must add up to 





Compare your answer with the correct one above
Triangle ABC has angle measures as follows:



What is  ?
?
Triangle ABC has angle measures as follows:
What is 
The sum of the measures of the angles of a triangle is 180.
Thus we set up the equation 
After combining like terms and cancelling, we have 
Thus 
The sum of the measures of the angles of a triangle is 180.
Thus we set up the equation
After combining like terms and cancelling, we have
Thus
Compare your answer with the correct one above
The base angle of an isosceles triangle is  . What is the vertex angle?
. What is the vertex angle?
The base angle of an isosceles triangle is 
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Solve the equation  for x to find the measure of the vertex angle.
for x to find the measure of the vertex angle.
x = 180 - 27 - 27
x = 126
Therefore the measure of the vertex angle is  .
.
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Solve the equation 
x = 180 - 27 - 27
x = 126
Therefore the measure of the vertex angle is 
Compare your answer with the correct one above
The base angle of an isosceles triangle is five more than twice the vertex angle. What is the base angle?
The base angle of an isosceles triangle is five more than twice the vertex angle. What is the base angle?
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let  = the vertex angle and
= the vertex angle and  = the base angle
= the base angle
So the equation to solve becomes 
Thus the vertex angle is 34 and the base angles are 73.
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let 

So the equation to solve becomes
Thus the vertex angle is 34 and the base angles are 73.
Compare your answer with the correct one above
Two interior angles in an obtuse triangle measure  and
and  . What is the measurement of the third angle.
. What is the measurement of the third angle.
Two interior angles in an obtuse triangle measure 

Interior angles of a triangle always add up to 180 degrees.
Interior angles of a triangle always add up to 180 degrees.
Compare your answer with the correct one above
The base angle of an isosceles triangle is 15 less than three times the vertex angle. What is the vertex angle?
The base angle of an isosceles triangle is 15 less than three times the vertex angle. What is the vertex angle?
Every triangle contains 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let  = vertex angle and
= vertex angle and  = base angle
= base angle
So the equation to solve becomes  .
.
Every triangle contains 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let 

So the equation to solve becomes 
Compare your answer with the correct one above
The base angle of an isosceles triangle is ten less than twice the vertex angle. What is the vertex angle?
The base angle of an isosceles triangle is ten less than twice the vertex angle. What is the vertex angle?
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let  = vertex angle and
= vertex angle and  = base angle
= base angle
So the equation to solve becomes 
So the vertex angle is 40 and the base angles is 70
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let 

So the equation to solve becomes
So the vertex angle is 40 and the base angles is 70
Compare your answer with the correct one above
The base angle of an isosceles triangle is 10 more than twice the vertex angle. What is the vertex angle?
The base angle of an isosceles triangle is 10 more than twice the vertex angle. What is the vertex angle?
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let  = the vertex angle and
= the vertex angle and  = the base angle
= the base angle
So the equation to solve becomes 
The vertex angle is 32 degrees and the base angle is 74 degrees
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let 

So the equation to solve becomes
The vertex angle is 32 degrees and the base angle is 74 degrees
Compare your answer with the correct one above
In an isosceles triangle, the vertex angle is 15 less than the base angle. What is the base angle?
In an isosceles triangle, the vertex angle is 15 less than the base angle. What is the base angle?
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let  = base angle and
= base angle and  = vertex angle
= vertex angle
So the equation to solve becomes 
Thus, 65 is the base angle and 50 is the vertex angle.
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let 

So the equation to solve becomes
Thus, 65 is the base angle and 50 is the vertex angle.
Compare your answer with the correct one above
In a given triangle, the angles are in a ratio of 1:3:5. What size is the middle angle?
In a given triangle, the angles are in a ratio of 1:3:5. What size is the middle angle?
Since the sum of the angles of a triangle is  , and given that the angles are in a ratio of 1:3:5, let the measure of the smallest angle be
, and given that the angles are in a ratio of 1:3:5, let the measure of the smallest angle be  , then the following expression could be written:
, then the following expression could be written:



If the smallest angle is 20 degrees, then given that the middle angle is in ratio of 1:3, the middle angle would be 3 times as large, or 60 degrees.
Since the sum of the angles of a triangle is 

If the smallest angle is 20 degrees, then given that the middle angle is in ratio of 1:3, the middle angle would be 3 times as large, or 60 degrees.
Compare your answer with the correct one above
In an isosceles triangle the vertex angle is half the base angle. What is the vertex angle?
In an isosceles triangle the vertex angle is half the base angle. What is the vertex angle?
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let  = base angle and
= base angle and  = vertex angle
= vertex angle
So the equation to solve becomes  , thus
, thus  is the base angle and
is the base angle and  is the vertex angle.
is the vertex angle.
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let 

So the equation to solve becomes 


Compare your answer with the correct one above

In the picture above,  is a straight line segment. Find the value of
is a straight line segment. Find the value of  .
.

In the picture above, 

A straight line segment has 180 degrees. Therefore, the angle that is not labelled must have:

We know that the sum of the angles in a triangle is 180 degrees. As a result, we can set up the following algebraic equation:

Subtract 70 from both sides:

Divide by 2:

A straight line segment has 180 degrees. Therefore, the angle that is not labelled must have:
We know that the sum of the angles in a triangle is 180 degrees. As a result, we can set up the following algebraic equation:
Subtract 70 from both sides:
Divide by 2:
Compare your answer with the correct one above
Solve for  . (Not drawn to scale).
. (Not drawn to scale).
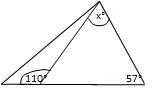
Solve for 

The angles of a triangle must add to 180o. In the triangle to the right, we know one angle and can find another using supplementary angles.

Now we only need to solve for  .
.



The angles of a triangle must add to 180o. In the triangle to the right, we know one angle and can find another using supplementary angles.
Now we only need to solve for 
Compare your answer with the correct one above

 . The measure of angle CBD is
. The measure of angle CBD is  . The length of segment
. The length of segment  is 4.
is 4. .
.