Taylor and Maclaurin Series - High School Math

Card 0 of 5

Question

Give the $x^{2}$ term of the Maclaurin series expansion of the function $f (x) = 7 ^{x}$ .

Answer

The $x^{2}$ term of a Maclaurin series expansion has coefficient

$\frac{f ' ' (0)}{2!} = \frac{f ' ' (0)}{2}$ .

We can find by differentiating twice in succession:

$f (x) = 7^{x}$

$f ' (x) = \frac{\mathrm{d} }{\mathrm{d} x} \left ( 7^{x} \right )= \ln 7 \cdot 7^{x}$

$f ' '(x) = \frac{\mathrm{d} }{\mathrm{d} x} \left (\ln 7 \cdot 7^{x} \right )$

$f ' '(x)= \ln 7\cdot \frac{\mathrm{d} }{\mathrm{d} x} \left ( 7^{x} \right )$

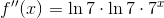
$f ' '(x)= \ln 7\cdot \ln 7\cdot 7^{x}$

$f ' '(x)=\left ( \ln 7 \right )^{2} \cdot 7^{x}$

$f ' '(0)=\left ( \ln 7 \right )^{2} \cdot 7^{0} = \left ( \ln 7 \right )^{2} \cdot 1 = \left ( \ln 7 \right )^{2}$

The coefficient we want is

$\frac{f ' ' (0)}{2} =\frac{\left ( \ln 7 \right )^{2}}{2}$ ,

so the corresponding term is $\frac{\left ( \ln 7 \right )^{2}}{2} x^{2}$ .

Compare your answer with the correct one above

Question

Give the $x^{4}$ term of the Maclaurin series expansion of the function $f(x) = x \tan^{-1} x$ .

Answer

This can most easily be answered by recalling that the Maclaurin series for $\tan^{-1} x$ is

$\tan^{-1} x = x - \frac{1}{3} x^{3 } + \frac{1}{5} x^{5 }...$

Multiply by to get:

$x\tan^{-1} x = x\cdot x - x\cdot \frac{1}{3} x^{3 } + x\cdot \frac{1}{5} x^{5 }...$

$x \tan^{-1} x=x^{2 } - \frac{1}{3} x^{4 } + \frac{1}{5} x^{6 }...$

The $x^{4}$ term is therefore $- \frac{1}{3} x^{4 }$ .

Compare your answer with the correct one above

Question

Give the $x^ {3}$ term of the Maclaurin series of the function $f(x) = \sinh 3x$ .

Answer

The $x^ {3}$ term of a Maclaurin series expansion has coefficient

$\frac{f ' '' (0)}{3!} = \frac{f ' '' (0)}{6}$ .

We can find by differentiating three times in succession:

$f(x) = \sinh 3x$

$f'(x) = 3 \cosh 3x$

$f''(x) = 3\cdot 3\sinh 3x = 9\sinh 3x$

$f'''(x) = 9 \cdot 3\cosh 3x = 27 \cosh 3x$

$f'''(0) = 27 \cosh \left (3 \cdot 0 \right ) = 27 \cosh 0 = 27\cdot 1 = 27$

The term we want is therefore

$\frac{f ' '' (0)}{6} \cdot x^{3} = \frac{27}{6} \cdot x^{3} = \frac{9}{2} x^{3}$

Compare your answer with the correct one above

Question

Give the $x^{2}$ term of the Maclaurin series of the function $f \left ( x\right ) = \frac{1}{x-2}$

Answer

The $x^{2}$ term of the Maclaurin series of a function has coefficient $\frac{f '' (0) }{2!} = \frac{f '' (0) }{2}$

The second derivative of can be found as follows:

$f \left ( x\right ) = \frac{1}{x-2} = (x-2) ^{-1}$

$f' \left ( x\right ) = -1\cdot (x-2)^{-2} = -1(x-2)^{-2}$

$f'' \left ( x\right ) = (-2) ( -1(x-2)^{-3}) = 2(x-2)^{-3} = \frac{2}{(x-2)^{3}}$

$f'' \left ( 0 \right ) =\frac{2}{(0-2)^{3}} = -\frac{1}{4}$

The coeficient of $x^{2}$ in the Maclaurin series is therefore

$\frac{f '' (0) }{2} = \frac{-\frac{1}{4}}{2} = - \frac{1}{8}$

Compare your answer with the correct one above

Question

Give the term of the Taylor series expansion of the function $f (x) = \log_5 x$ about .

Answer

The $(x-1)^{2}$ term of a Taylor series expansion about is

$\frac{f ' ' (1)}{2!} (x-1)^{2}= \frac{f ' ' (1)}{2}(x-1)^{2}$ .

We can find by differentiating twice in succession:

$f (x) = \log_5 x$

$f'(x) = \frac{1}{x \ln 5}$

$f'(x) =\frac{1}{ \ln 5} \cdot x^{-1}$

$f''(x) = \frac{\mathrm{d} }{\mathrm{d} x}\left (\frac{1}{ \ln 5} \cdot x^{-1} \right )$

$f''(x) =\frac{1}{ \ln 5}\cdot \frac{\mathrm{d} }{\mathrm{d} x}\left ( x^{-1} \right )$

$f''(x) =\frac{1}{ \ln 5} \cdot \left ( -1 \cdot x^{-2} \right )$

$f''(x) =- \frac{1}{ \ln 5 \cdot x^{2}}$

$f''(1) =- \frac{1}{ \ln 5 \cdot 1^{2}} = - \frac{1}{ \ln 5 }$

so the term is $\frac{f''(1) }{2} ; (x-1)^{2} = - \frac{1}{2 \ln 5 } (x-1)^{2} = - \frac{1}{ \ln 25 } (x-1)^{2}$

Compare your answer with the correct one above

Tap the card to reveal the answer