Functions and Graphs - High School Math
Card 0 of 20
A function is defined by the following rational equation:

What are the horizontal and vertical asymptotes of this function's graph?
A function is defined by the following rational equation:
What are the horizontal and vertical asymptotes of this function's graph?
To find the horizontal asymptote, compare the degrees of the top and bottom polynomials. In this case, the two degrees are the same (1), which means that the equation of the horizontal asymptote is equal to the ratio of the leading coefficients (top : bottom). Since the numerator's leading coefficient is 1, and the denominator's leading coefficient is 2, the equation of the horizontal asymptote is  .
.
To find the vertical asymptote, set the denominator equal to zero to find when the entire function is undefined:



To find the horizontal asymptote, compare the degrees of the top and bottom polynomials. In this case, the two degrees are the same (1), which means that the equation of the horizontal asymptote is equal to the ratio of the leading coefficients (top : bottom). Since the numerator's leading coefficient is 1, and the denominator's leading coefficient is 2, the equation of the horizontal asymptote is 
To find the vertical asymptote, set the denominator equal to zero to find when the entire function is undefined:
Compare your answer with the correct one above
A function is defined by the following rational equation:

What line does  approach as
approach as  approaches infinity?
approaches infinity?
A function is defined by the following rational equation:
What line does 

This question is asking for the equation's slant asymptote. To find the slant asymptote, divide the numerator by the denominator. Long division gives us the following:

However, because we are considering  as it approaches infinity, the effect that the last term has on the overall linear equation quickly becomes negligible (tends to zero). Thus, it can be ignored.
as it approaches infinity, the effect that the last term has on the overall linear equation quickly becomes negligible (tends to zero). Thus, it can be ignored.
This question is asking for the equation's slant asymptote. To find the slant asymptote, divide the numerator by the denominator. Long division gives us the following:
However, because we are considering 
Compare your answer with the correct one above
What is the domain of the function below:
![f(x)=\frac{1}{\sqrt[4]{x^{2}+1}-\frac{1}{2}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/138723/gif.latex)
What is the domain of the function below:
The domain is defined as the set of possible values for the x variable. In order to find the impossible values of x, we should:
a) Set the equation under the radical equal to zero and look for probable x values that make the expression inside the radical negative:


There is no real value for x that will fit this equation, because any real value square is a positive number i.e. cannot be a negative number.
b) Set the denominator of the fractional function equal to zero and look for probable x values:
![\sqrt[4]{x^2+1}-\frac{1}{2}=0](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/93233/gif.latex)
Now we can solve the equation for x:

There is no real value for x that will fit this equation.
The radical is always positive and denominator is never equal to zero, so the f(x) is defined for all real values of x. That means the set of all real numbers is the domain of the f(x) and the correct answer is  .
.
Alternative solution for the second part of the solution:
After figuring out that the expression under the radical is always positive (part a), we can solve the radical and therefore denominator for the least possible value (minimum value). Setting the x value equal to zero will give the minimum possible value for the denominator.

![\sqrt[4]{x^2+1}-\frac{1}{2}=](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/93235/gif.latex)
![\sqrt[4]{0+1}-\frac{1}{2}=](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/138727/gif.latex)

That means the denominator will always be a positive value greater than 1/2; thus it cannot be equal to zero by setting any real value for x. Therefore the set of all real numbers is the domain of the f(x).
The domain is defined as the set of possible values for the x variable. In order to find the impossible values of x, we should:
a) Set the equation under the radical equal to zero and look for probable x values that make the expression inside the radical negative:
There is no real value for x that will fit this equation, because any real value square is a positive number i.e. cannot be a negative number.
b) Set the denominator of the fractional function equal to zero and look for probable x values:
Now we can solve the equation for x:
There is no real value for x that will fit this equation.
The radical is always positive and denominator is never equal to zero, so the f(x) is defined for all real values of x. That means the set of all real numbers is the domain of the f(x) and the correct answer is 
Alternative solution for the second part of the solution:
After figuring out that the expression under the radical is always positive (part a), we can solve the radical and therefore denominator for the least possible value (minimum value). Setting the x value equal to zero will give the minimum possible value for the denominator.
That means the denominator will always be a positive value greater than 1/2; thus it cannot be equal to zero by setting any real value for x. Therefore the set of all real numbers is the domain of the f(x).
Compare your answer with the correct one above
What is the domain of the function below?

What is the domain of the function below?
The domain is defined as the set of all values of x for which the function is defined i.e. has a real result. The square root of a negative number isn't defined, so we should find the intervals where that occurs:

The square of any number is positive, so we can't eliminate any x-values yet.
If the denominator is zero, the expression will also be undefined.
Find the x-values which would make the denominator 0:

Therefore, the domain is  .
.
The domain is defined as the set of all values of x for which the function is defined i.e. has a real result. The square root of a negative number isn't defined, so we should find the intervals where that occurs:
The square of any number is positive, so we can't eliminate any x-values yet.
If the denominator is zero, the expression will also be undefined.
Find the x-values which would make the denominator 0:
Therefore, the domain is 
Compare your answer with the correct one above
What is the domain of the function below:

What is the domain of the function below:
The domain is defined as the set of all possible values of the independent variable  . First,
. First,  must be greater than or equal to zero, because if
must be greater than or equal to zero, because if  , then
, then will be undefined. In addition, the total expression under the radical, i.e.
will be undefined. In addition, the total expression under the radical, i.e.  must be greater than or equal to zero:
must be greater than or equal to zero:




That means that the expression under the radical is always positive and therefore  is defined. Hence, the domain of the function
is defined. Hence, the domain of the function  is
is  .
.
The domain is defined as the set of all possible values of the independent variable 




That means that the expression under the radical is always positive and therefore 


Compare your answer with the correct one above
Consider the function

Find the maximum of the function on the interval ![\left [ 0,1 \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/90593/gif.latex) .
.
Consider the function
Find the maximum of the function on the interval ![\left [ 0,1 \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/90593/gif.latex)
Notice that on the interval ![\left [ 0,1 \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/90594/gif.latex) , the term
, the term  is always less than or equal to
is always less than or equal to  . So the function is largest at the points when
. So the function is largest at the points when  . This occurs at
. This occurs at  and
and  .
.
Plugging in either 1 or 0 into the original function  yields the correct answer of 0.
yields the correct answer of 0.
Notice that on the interval ![\left [ 0,1 \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/90594/gif.latex)





Plugging in either 1 or 0 into the original function 
Compare your answer with the correct one above
The function  is such that
is such that

When you take the second derivative of the function  , you obtain
, you obtain

What can you conclude about the function at  ?
?
The function 
When you take the second derivative of the function 
What can you conclude about the function at 
We have a point at which  . We know from the second derivative test that if the second derivative is negative, the function has a maximum at that point. If the second derivative is positive, the function has a minimum at that point. If the second derivative is zero, the function has an inflection point at that point.
. We know from the second derivative test that if the second derivative is negative, the function has a maximum at that point. If the second derivative is positive, the function has a minimum at that point. If the second derivative is zero, the function has an inflection point at that point.
Plug in 0 into the second derivative to obtain

So the point is an inflection point.
We have a point at which 
Plug in 0 into the second derivative to obtain
So the point is an inflection point.
Compare your answer with the correct one above

This function is:
This function is:
A function's symmetry is related to its classification as even, odd, or neither.
Even functions obey the following rule:

Because of this, even functions are symmetric about the y-axis.
Odd functions obey the following rule:

Because of this, odd functions are symmetric about the origin.
If a function does not obey either rule, it is neither odd nor even. (A graph that is symmetric about the x-axis is not a function, because it does not pass the vertical line test.)
To test for symmetry, simply substitute  into the original equation.
into the original equation.

Thus, this equation is even and therefore symmetric about the y-axis.
A function's symmetry is related to its classification as even, odd, or neither.
Even functions obey the following rule:
Because of this, even functions are symmetric about the y-axis.
Odd functions obey the following rule:
Because of this, odd functions are symmetric about the origin.
If a function does not obey either rule, it is neither odd nor even. (A graph that is symmetric about the x-axis is not a function, because it does not pass the vertical line test.)
To test for symmetry, simply substitute 
Thus, this equation is even and therefore symmetric about the y-axis.
Compare your answer with the correct one above
Find the zeros of the following polynomial:

Find the zeros of the following polynomial:
First, we need to find all the possible rational roots of the polynomial using the Rational Roots Theorem:

Since the leading coefficient is just 1, we have the following possible (rational) roots to try:
±1, ±2, ±3, ±4, ±6, ±12, ±24
When we substitute one of these numbers for  , we're hoping that the equation ends up equaling zero. Let's see if
, we're hoping that the equation ends up equaling zero. Let's see if  is a zero:
is a zero:
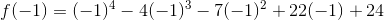


Since the function equals zero when  is
is  , one of the factors of the polynomial is
, one of the factors of the polynomial is  . This doesn't help us find the other factors, however. We can use synthetic substitution as a shorter way than long division to factor the equation.
. This doesn't help us find the other factors, however. We can use synthetic substitution as a shorter way than long division to factor the equation.



Now we can factor the function this way:
(x%5E%7B3%7D-5x%5E%7B2%7D-2x+24))
We repeat this process, using the Rational Roots Theorem with the second term to find a possible zero. Let's try  :
:
![f(-2)=[(-2)+1][(-2)^{3}-5(-2)^{2}-2(-2)+24]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/106228/gif.latex)

When we factor using synthetic substitution for  , we get the following result:
, we get the following result:

Using our quadratic factoring rules, we can factor completely:

Thus, the zeroes of  are
are 
First, we need to find all the possible rational roots of the polynomial using the Rational Roots Theorem:
Since the leading coefficient is just 1, we have the following possible (rational) roots to try:
±1, ±2, ±3, ±4, ±6, ±12, ±24
When we substitute one of these numbers for 

Since the function equals zero when 


Now we can factor the function this way:
We repeat this process, using the Rational Roots Theorem with the second term to find a possible zero. Let's try 
When we factor using synthetic substitution for 
Using our quadratic factoring rules, we can factor completely:
Thus, the zeroes of 
Compare your answer with the correct one above
What is the shape of the graph indicated by the equation?

What is the shape of the graph indicated by the equation?
An ellipse has an equation that can be written in the format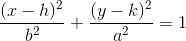 . The center is indicated by
. The center is indicated by 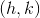 , or in this case
, or in this case  .
.
An ellipse has an equation that can be written in the format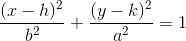
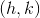

Compare your answer with the correct one above
A conic section is represented by the following equation:

Which of the following best describes this equation?
A conic section is represented by the following equation:
Which of the following best describes this equation?
First, we need to make sure the conic section equation is in a form we recognize. Luckily, this equation is already in standard form:

The first step is to determine the type of conic section this equation represents. Because there are two squared variables ( and
and  ), this equation cannot be a parabola. Because the coefficients in front of the squared variables are different signs (i.e. one is negative and the other is positive), this equation must be a hyperbola, not an ellipse.
), this equation cannot be a parabola. Because the coefficients in front of the squared variables are different signs (i.e. one is negative and the other is positive), this equation must be a hyperbola, not an ellipse.
In a hyperbola, the squared term with a positive coefficient represents the direction in which the hyperbola opens. In other words, if the  term is positive, the hyperbola opens horizontally. If the
term is positive, the hyperbola opens horizontally. If the  term is positive, the hyperbola opens vertically. Therefore, this is a horizontal hyperbola.
term is positive, the hyperbola opens vertically. Therefore, this is a horizontal hyperbola.
The center is always found at  , which in this case is
, which in this case is  .
.
That leaves only the asymptotes. For a hyperbola, the slopes of the asymptotes can be found by dividing  by
by  (remember to always put the vertical value,
(remember to always put the vertical value,  , above the horizontal value,
, above the horizontal value,  ). Remember that these slopes always come in pairs, with one being positive and the other being negative.
). Remember that these slopes always come in pairs, with one being positive and the other being negative.
In this case,  is 3 and
is 3 and  is 2, so we get slopes of
is 2, so we get slopes of  and
and  .
.
First, we need to make sure the conic section equation is in a form we recognize. Luckily, this equation is already in standard form:
The first step is to determine the type of conic section this equation represents. Because there are two squared variables (

In a hyperbola, the squared term with a positive coefficient represents the direction in which the hyperbola opens. In other words, if the 

The center is always found at 

That leaves only the asymptotes. For a hyperbola, the slopes of the asymptotes can be found by dividing 



In this case, 



Compare your answer with the correct one above
What is the minimal value of

over all real numbers?
What is the minimal value of
over all real numbers?
Since this is an upwards-opening parabola, its minimum value will occur at the vertex. The  -coordinate for the vertex of any parabola of the form
-coordinate for the vertex of any parabola of the form

is at
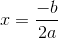
So here,



We plug this value back into the equation of the parabola, to find the value of the function at this 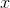 .
.

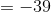
Thus the minimal value of the expression is  .
.
Since this is an upwards-opening parabola, its minimum value will occur at the vertex. The 
is at
So here,
We plug this value back into the equation of the parabola, to find the value of the function at this 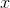
Thus the minimal value of the expression is 
Compare your answer with the correct one above
Compare your answer with the correct one above
Solve for  :
: 
Solve for 

![\log_{2} \left[ \left ( x+4 \right )\left ( x+5 \right ) \right ] = \log_{2} 6](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/99587/gif.latex)
![2^{ \log_{2} \left[ \left ( x+4 \right )\left ( x+5 \right ) \right ] }=2^{ \log_{2} 6}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/115528/gif.latex)

FOIL: 






These are our possible solutions. However, we need to test them.
 :
:






The equation becomes  . This is true, so
. This is true, so  is a solution.
is a solution.
 :
:



However, negative numbers do not have logarithms, so this equation is meaningless.  is not a solution, and
is not a solution, and  is the one and only solution. Since this is not one of our choices, the correct response is "The correct solution set is not included among the other choices."
is the one and only solution. Since this is not one of our choices, the correct response is "The correct solution set is not included among the other choices."
FOIL:
These are our possible solutions. However, we need to test them.

The equation becomes 


However, negative numbers do not have logarithms, so this equation is meaningless. 

Compare your answer with the correct one above
Simplify the following polynomial function:

Simplify the following polynomial function:
First, multiply the outside term with each term within the parentheses:


Rearranging the polynomial into fractional form, we get:

First, multiply the outside term with each term within the parentheses:
Rearranging the polynomial into fractional form, we get:
Compare your answer with the correct one above
Simplify the following polynomial:

Simplify the following polynomial:
To simplify the polynomial, begin by combining like terms:


To simplify the polynomial, begin by combining like terms:
Compare your answer with the correct one above
What is the center and radius of the circle indicated by the equation?

What is the center and radius of the circle indicated by the equation?
A circle is defined by an equation in the format  .
.
The center is indicated by the point  and the radius
and the radius  .
.
In the equation  , the center is
, the center is  and the radius is
and the radius is  .
.
A circle is defined by an equation in the format 
The center is indicated by the point 

In the equation 


Compare your answer with the correct one above
A conic section is represented by the following equation:

What type of conic section does this equation represent?
A conic section is represented by the following equation:
What type of conic section does this equation represent?
The simplest way to know what kind of conic section an equation represents is by checking the coefficients in front of each variable. The equation must be in general form while you do this check. Luckily, this equation is already in general form, so it's easy to see. The general equation for a conic section is the following:

Assuming the term  is 0 (which it usually is):
is 0 (which it usually is):
- If A equals C, the equation is a circle.
- If A and C have the same sign (but are not equal to each other), the equation is an ellipse.
- If either A or C equals 0, the equation is a parabola.
- If A and C are different signs (i.e. one is negative and one is positive), the equation is a hyperbola.
The simplest way to know what kind of conic section an equation represents is by checking the coefficients in front of each variable. The equation must be in general form while you do this check. Luckily, this equation is already in general form, so it's easy to see. The general equation for a conic section is the following:
Assuming the term 
- If A equals C, the equation is a circle.
- If A and C have the same sign (but are not equal to each other), the equation is an ellipse.
- If either A or C equals 0, the equation is a parabola.
- If A and C are different signs (i.e. one is negative and one is positive), the equation is a hyperbola.
Compare your answer with the correct one above
You are given that  and
and  .
.
Which of the following is equal to  ?
?
You are given that 

Which of the following is equal to 
Since  and
and  , it follows that
, it follows that  and
and 

Since 


Compare your answer with the correct one above
Compare your answer with the correct one above





