Pre-Calculus - High School Math
Card 0 of 20
A function is defined by the following rational equation:

What are the horizontal and vertical asymptotes of this function's graph?
A function is defined by the following rational equation:
What are the horizontal and vertical asymptotes of this function's graph?
To find the horizontal asymptote, compare the degrees of the top and bottom polynomials. In this case, the two degrees are the same (1), which means that the equation of the horizontal asymptote is equal to the ratio of the leading coefficients (top : bottom). Since the numerator's leading coefficient is 1, and the denominator's leading coefficient is 2, the equation of the horizontal asymptote is  .
.
To find the vertical asymptote, set the denominator equal to zero to find when the entire function is undefined:



To find the horizontal asymptote, compare the degrees of the top and bottom polynomials. In this case, the two degrees are the same (1), which means that the equation of the horizontal asymptote is equal to the ratio of the leading coefficients (top : bottom). Since the numerator's leading coefficient is 1, and the denominator's leading coefficient is 2, the equation of the horizontal asymptote is 
To find the vertical asymptote, set the denominator equal to zero to find when the entire function is undefined:
Compare your answer with the correct one above
A function is defined by the following rational equation:

What line does  approach as
approach as  approaches infinity?
approaches infinity?
A function is defined by the following rational equation:
What line does 

This question is asking for the equation's slant asymptote. To find the slant asymptote, divide the numerator by the denominator. Long division gives us the following:

However, because we are considering  as it approaches infinity, the effect that the last term has on the overall linear equation quickly becomes negligible (tends to zero). Thus, it can be ignored.
as it approaches infinity, the effect that the last term has on the overall linear equation quickly becomes negligible (tends to zero). Thus, it can be ignored.
This question is asking for the equation's slant asymptote. To find the slant asymptote, divide the numerator by the denominator. Long division gives us the following:
However, because we are considering 
Compare your answer with the correct one above
What is the domain of the function below:
![f(x)=\frac{1}{\sqrt[4]{x^{2}+1}-\frac{1}{2}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/138723/gif.latex)
What is the domain of the function below:
The domain is defined as the set of possible values for the x variable. In order to find the impossible values of x, we should:
a) Set the equation under the radical equal to zero and look for probable x values that make the expression inside the radical negative:


There is no real value for x that will fit this equation, because any real value square is a positive number i.e. cannot be a negative number.
b) Set the denominator of the fractional function equal to zero and look for probable x values:
![\sqrt[4]{x^2+1}-\frac{1}{2}=0](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/93233/gif.latex)
Now we can solve the equation for x:

There is no real value for x that will fit this equation.
The radical is always positive and denominator is never equal to zero, so the f(x) is defined for all real values of x. That means the set of all real numbers is the domain of the f(x) and the correct answer is  .
.
Alternative solution for the second part of the solution:
After figuring out that the expression under the radical is always positive (part a), we can solve the radical and therefore denominator for the least possible value (minimum value). Setting the x value equal to zero will give the minimum possible value for the denominator.

![\sqrt[4]{x^2+1}-\frac{1}{2}=](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/93235/gif.latex)
![\sqrt[4]{0+1}-\frac{1}{2}=](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/138727/gif.latex)

That means the denominator will always be a positive value greater than 1/2; thus it cannot be equal to zero by setting any real value for x. Therefore the set of all real numbers is the domain of the f(x).
The domain is defined as the set of possible values for the x variable. In order to find the impossible values of x, we should:
a) Set the equation under the radical equal to zero and look for probable x values that make the expression inside the radical negative:
There is no real value for x that will fit this equation, because any real value square is a positive number i.e. cannot be a negative number.
b) Set the denominator of the fractional function equal to zero and look for probable x values:
Now we can solve the equation for x:
There is no real value for x that will fit this equation.
The radical is always positive and denominator is never equal to zero, so the f(x) is defined for all real values of x. That means the set of all real numbers is the domain of the f(x) and the correct answer is 
Alternative solution for the second part of the solution:
After figuring out that the expression under the radical is always positive (part a), we can solve the radical and therefore denominator for the least possible value (minimum value). Setting the x value equal to zero will give the minimum possible value for the denominator.
That means the denominator will always be a positive value greater than 1/2; thus it cannot be equal to zero by setting any real value for x. Therefore the set of all real numbers is the domain of the f(x).
Compare your answer with the correct one above
What is the domain of the function below?

What is the domain of the function below?
The domain is defined as the set of all values of x for which the function is defined i.e. has a real result. The square root of a negative number isn't defined, so we should find the intervals where that occurs:

The square of any number is positive, so we can't eliminate any x-values yet.
If the denominator is zero, the expression will also be undefined.
Find the x-values which would make the denominator 0:

Therefore, the domain is  .
.
The domain is defined as the set of all values of x for which the function is defined i.e. has a real result. The square root of a negative number isn't defined, so we should find the intervals where that occurs:
The square of any number is positive, so we can't eliminate any x-values yet.
If the denominator is zero, the expression will also be undefined.
Find the x-values which would make the denominator 0:
Therefore, the domain is 
Compare your answer with the correct one above
What is the domain of the function below:

What is the domain of the function below:
The domain is defined as the set of all possible values of the independent variable  . First,
. First,  must be greater than or equal to zero, because if
must be greater than or equal to zero, because if  , then
, then will be undefined. In addition, the total expression under the radical, i.e.
will be undefined. In addition, the total expression under the radical, i.e.  must be greater than or equal to zero:
must be greater than or equal to zero:




That means that the expression under the radical is always positive and therefore  is defined. Hence, the domain of the function
is defined. Hence, the domain of the function  is
is  .
.
The domain is defined as the set of all possible values of the independent variable 




That means that the expression under the radical is always positive and therefore 


Compare your answer with the correct one above
Evaluate the limit below:

Evaluate the limit below:
 will approach
will approach  when
when  approaches
approaches  , so
, so 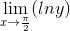 will be of type
will be of type  as shown below:
as shown below:

So, we can apply the L’ Hospital's Rule:


since:

hence:





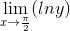

So, we can apply the L’ Hospital's Rule:
since:
hence:
Compare your answer with the correct one above
The speed of a car traveling on the highway is given by the following function of time:

What can you say about the car's speed after a long time (that is, as  approaches infinity)?
approaches infinity)?
The speed of a car traveling on the highway is given by the following function of time:
What can you say about the car's speed after a long time (that is, as 
The function given is a polynomial with a term  , such that
, such that  is greater than 1.
is greater than 1.
Whenever this is the case, we can say that the whole function diverges (approaches infinity) in the limit as  approaches infinity.
approaches infinity.
This tells us that the given function is not a very realistic description of a car's speed for large  !
!
The function given is a polynomial with a term 

Whenever this is the case, we can say that the whole function diverges (approaches infinity) in the limit as 
This tells us that the given function is not a very realistic description of a car's speed for large 
Compare your answer with the correct one above
Compare your answer with the correct one above
Calculate  .
.
Calculate 
This can be rewritten as follows:


![= \lim_{x\rightarrow \infty }\left [\left ( x^{2}-1 \right ) \cdot \sin \frac{1}{ x^{2}-1} \right]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/99922/gif.latex)

We can substitute  , noting that as
, noting that as  ,
,  :
:
 , which is the correct choice.
, which is the correct choice.
This can be rewritten as follows:
We can substitute 



Compare your answer with the correct one above
Consider the function

Find the maximum of the function on the interval ![\left [ 0,1 \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/90593/gif.latex) .
.
Consider the function
Find the maximum of the function on the interval ![\left [ 0,1 \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/90593/gif.latex)
Notice that on the interval ![\left [ 0,1 \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/90594/gif.latex) , the term
, the term  is always less than or equal to
is always less than or equal to  . So the function is largest at the points when
. So the function is largest at the points when  . This occurs at
. This occurs at  and
and  .
.
Plugging in either 1 or 0 into the original function  yields the correct answer of 0.
yields the correct answer of 0.
Notice that on the interval ![\left [ 0,1 \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/90594/gif.latex)





Plugging in either 1 or 0 into the original function 
Compare your answer with the correct one above
The function  is such that
is such that

When you take the second derivative of the function  , you obtain
, you obtain

What can you conclude about the function at  ?
?
The function 
When you take the second derivative of the function 
What can you conclude about the function at 
We have a point at which  . We know from the second derivative test that if the second derivative is negative, the function has a maximum at that point. If the second derivative is positive, the function has a minimum at that point. If the second derivative is zero, the function has an inflection point at that point.
. We know from the second derivative test that if the second derivative is negative, the function has a maximum at that point. If the second derivative is positive, the function has a minimum at that point. If the second derivative is zero, the function has an inflection point at that point.
Plug in 0 into the second derivative to obtain

So the point is an inflection point.
We have a point at which 
Plug in 0 into the second derivative to obtain
So the point is an inflection point.
Compare your answer with the correct one above
Let  .
.
Find  .
.
Let 
Find 

This is a graph of  . We know that
. We know that  is undefined; therefore, there is no value for
is undefined; therefore, there is no value for  . But as we take a look at the graph, we can see that as
. But as we take a look at the graph, we can see that as  approaches 0 from the left,
approaches 0 from the left,  approaches negative infinity.
approaches negative infinity.
This can be illustrated by thinking of small negative numbers.


NOTE: Pay attention to one-sided limit specifications, as it is easy to pick the wrong answer choice if you're not careful.
 is actually infinity, not negative infinity.
is actually infinity, not negative infinity.

This is a graph of 




This can be illustrated by thinking of small negative numbers.
NOTE: Pay attention to one-sided limit specifications, as it is easy to pick the wrong answer choice if you're not careful.

Compare your answer with the correct one above
Find the sum of all even integers from  to
to  .
.
Find the sum of all even integers from 

The formula for the sum of an arithmetic series is
 ,
,
where  is the number of terms in the series,
is the number of terms in the series,  is the first term, and
is the first term, and  is the last term.
is the last term.

The formula for the sum of an arithmetic series is

where 


Compare your answer with the correct one above
Find the sum of all even integers from  to
to  .
.
Find the sum of all even integers from 

The formula for the sum of an arithmetic series is
 ,
,
where  is the number of terms in the series,
is the number of terms in the series,  is the first term, and
is the first term, and  is the last term.
is the last term.
We know that there are  terms in the series. The first term is
terms in the series. The first term is  and the last term is
and the last term is  . Our formula becomes:
. Our formula becomes:


The formula for the sum of an arithmetic series is

where 


We know that there are 


Compare your answer with the correct one above
Find the sum of the even integers from  to
to  .
.
Find the sum of the even integers from 

The sum of even integers represents an arithmetic series.
The formula for the partial sum of an arithmetic series is
 ,
,
where  is the first value in the series,
is the first value in the series,  is the number of terms, and
is the number of terms, and  is the difference between sequential terms.
is the difference between sequential terms.
Plugging in our values, we get:



The sum of even integers represents an arithmetic series.
The formula for the partial sum of an arithmetic series is

where 


Plugging in our values, we get:
Compare your answer with the correct one above
Find the value for 
Find the value for
To best understand, let's write out the series. So

We can see this is an infinite geometric series with each successive term being multiplied by  .
.
A definition you may wish to remember is
 where
where  stands for the common ratio between the numbers, which in this case is
stands for the common ratio between the numbers, which in this case is  or
or  . So we get
. So we get

To best understand, let's write out the series. So
We can see this is an infinite geometric series with each successive term being multiplied by 
A definition you may wish to remember is




Compare your answer with the correct one above
Evaluate:

Evaluate:
This is a geometric series whose first term is  and whose common ratio is
and whose common ratio is  . The sum of this series is:
. The sum of this series is:

This is a geometric series whose first term is 

Compare your answer with the correct one above
Evaluate:

Evaluate:
This is a geometric series whose first term is  and whose common ratio is
and whose common ratio is  . The sum of this series is:
. The sum of this series is:

This is a geometric series whose first term is 

Compare your answer with the correct one above

This function is:
This function is:
A function's symmetry is related to its classification as even, odd, or neither.
Even functions obey the following rule:

Because of this, even functions are symmetric about the y-axis.
Odd functions obey the following rule:

Because of this, odd functions are symmetric about the origin.
If a function does not obey either rule, it is neither odd nor even. (A graph that is symmetric about the x-axis is not a function, because it does not pass the vertical line test.)
To test for symmetry, simply substitute  into the original equation.
into the original equation.

Thus, this equation is even and therefore symmetric about the y-axis.
A function's symmetry is related to its classification as even, odd, or neither.
Even functions obey the following rule:
Because of this, even functions are symmetric about the y-axis.
Odd functions obey the following rule:
Because of this, odd functions are symmetric about the origin.
If a function does not obey either rule, it is neither odd nor even. (A graph that is symmetric about the x-axis is not a function, because it does not pass the vertical line test.)
To test for symmetry, simply substitute 
Thus, this equation is even and therefore symmetric about the y-axis.
Compare your answer with the correct one above
Consider the sequence: 
What is the fifteenth term in the sequence?
Consider the sequence:
What is the fifteenth term in the sequence?
The sequence can be described by the equation  , where
, where  is the term in the sequence.
is the term in the sequence.
For the 15th term,  .
.




The sequence can be described by the equation 

For the 15th term, 
Compare your answer with the correct one above


