Whole Numbers - High School Math

First, distribute the negative sign into the parentheses.

Next, combine like terms.

Note that all operations in this problem are addition and subtraction; there is no need to FOIL or multiply.

To simplify a problem like the example above we must combine the like termed variables.

Like terms are the numbers that have the same variable, in this example, and .

Separate the 's to get .

Then perform the necessary subtraction to get .

Then separate the 's to get .

Then perform the necessary subtraction to get .

We then combine our answers to have the simplified version of the equation .

Re-write the expression to group like terms together.

Simplify.

To simplify a problem like the example above we must combine the like termed variables.

Like terms are the numbers that have the same variable, in this example, and .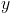

Separate the 's to get .

Then perform the necessary subtraction and addition with the numbers in front of the variables to get or .

Then separate the 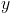’s to get .

Then perform the necessary subtraction to get .

We then combine our answers to have the simplified version of the equation .

To simplify a problem like the example above we must combine the like-termed variables.

Like terms are the terms that share the same variable(s) to the same power. In this example the like term is .

To combine like terms the variable stays the same and you add the numbers in front.

Perform the necessary addition, , to get .

We have the simplified version of the equation, .

When combining like terms, the order of operations must also be taken into account.

then combine the x squared terms to get the answer.

When you multiply exponents you can simply add the exponents:

We can solve this problem in two different ways.

The first way is to evaluate the internal term, , and then square it.

The second method is to use the power rule of exponents, where we multiply the exponents and solve the resulting term.

The negative sign in the exponent indicates that in order to solve you should use the reciprocal of the integer.

The laws of exponents state that when a number is raised to a certain power and then raised to another power then the exponents are multiplied by one another.

Solve for the exponents.

Therefore,

When a number is raised to a power it means that the number is multiplied by itself the same number of times as the number of the power.

In this case is raised to the power so it is equivalent to

We then perform the necessary multiplication to arrive at the answer of .

When a number is raised to a power it means that the number is multiplied by itself the same number of times as the number of the power.

In this case is raised to the power so it is equivalent to

We then perform the necessary multiplication to arrive at the answer of .

Because the exponent is negative, we have to move the decimal four places to the left. We need to add three zeroes between the decimal the number three.

Simplifying exponents with a common base can be done by subtracting the exponent in the denominator from the exponent in the numerator.

This gives us the final answer, .

A negative exponent can be written as a positive exponent in the denominator of a fraction.

Now we can evaluate the exponent and simplify.

Even though the base of the exponents are the same, you cannot add the exponents. You must perform each exponent separately.

Since the two bases of the exponents are the same and are being multiplied, it is acceptable to combine the terms and add their exponents resulting in which equals 128.

When you see an exponent, remember it just means the number times itself that many times. That means that is just another way to write .

From here, we can solve it all together in a calculator, or do it in pieces on our own.

Remember, an exponent just means the number times itself that many times.

That means that is just another way to write . From here, we can solve.