Integers - High School Math
Card 0 of 20
What is the difference between 8 and -2?
What is the difference between 8 and -2?
Since we want to find the difference between 8 and -2, we want to subtract -2 from 8. Since subtracting is equivalent to adding the same number with the opposite sign, we have the below:

Since we want to find the difference between 8 and -2, we want to subtract -2 from 8. Since subtracting is equivalent to adding the same number with the opposite sign, we have the below:
Compare your answer with the correct one above
Find the difference.

Find the difference.
We are subtracting here, so it is important to remember that subtracting is really just adding the same number with opposite sign. Thus we can think of the problem as the following:
 , which we know is equal to
, which we know is equal to  .
.
We are subtracting here, so it is important to remember that subtracting is really just adding the same number with opposite sign. Thus we can think of the problem as the following:


Compare your answer with the correct one above
What is  ?
?
What is 
Recall that subtracting integers is equivalent to adding the inverse. The inverse of a negative number is the positive number with the same magnitude.
Thus, our problem is equivalent to  .
.
Recall that subtracting integers is equivalent to adding the inverse. The inverse of a negative number is the positive number with the same magnitude.
Thus, our problem is equivalent to 
Compare your answer with the correct one above
Evaluate the following expression:

Evaluate the following expression:
Recall that subtracting is equivalent to adding the inverse:

The inverse of a negative number is a positive number:

Recall that subtracting is equivalent to adding the inverse:
The inverse of a negative number is a positive number:
Compare your answer with the correct one above
What is:

What is:
Recall the placement of numbers on the number line.  is
is  spaces to the left of
spaces to the left of  , and then we add
, and then we add  , resulting in movement to the right.
, resulting in movement to the right.
When we add these spaces we end up going  spaces back to
spaces back to  and then
and then  additional spaces to end at
additional spaces to end at  .
.
Recall the placement of numbers on the number line. 



When we add these spaces we end up going 



Compare your answer with the correct one above
What is  ?
?
What is 
Recall that subtracting a negative number is equivalent to adding the opposite. Thus, 
Recall that subtracting a negative number is equivalent to adding the opposite. Thus,
Compare your answer with the correct one above
What is  ?
?
What is 
Recall that subtracting negative numbers is equivalent to adding the opposite. Then, we have that:

Recall that subtracting negative numbers is equivalent to adding the opposite. Then, we have that:
Compare your answer with the correct one above
Simplify:

Simplify:
Combine like terms:

= (5 + 7) + (-2x - 4x - 9x)
= 12 + (-15x)
= 12 - 15x
Combine like terms:
= (5 + 7) + (-2x - 4x - 9x)
= 12 + (-15x)
= 12 - 15x
Compare your answer with the correct one above
Simplify:

Simplify:
To combine like terms, combine the numbers as you would a normal addition or subtraction problem:



Therefore,  = 8x - 8y.
= 8x - 8y.
To combine like terms, combine the numbers as you would a normal addition or subtraction problem:

Therefore, 
Compare your answer with the correct one above
What is the value of  ?
?
What is the value of 
Adding and subtracting negative integers is confusing if you don't use parentheses right. As long as you remember to keep them in the right places and stay neat, it is easy. Subtracting negative numbers is the same as adding a positive number, and adding a negative number is the same as subtracting a positive number. So, we could rewrite the equation like this:

Adding and subtracting negative integers is confusing if you don't use parentheses right. As long as you remember to keep them in the right places and stay neat, it is easy. Subtracting negative numbers is the same as adding a positive number, and adding a negative number is the same as subtracting a positive number. So, we could rewrite the equation like this:
Compare your answer with the correct one above
What is  simplified?
simplified?
What is 
To simplify a problem like the example above we must combine the like termed variables.
Like terms are the numbers that have the same variable, in this example,  and
and 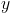 .
.
Separate the  s to get
s to get 
Then perform the necessary addition to get 
Then separate the 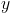 ’s to get
’s to get 
Then perform the necessary subtraction to get
We then combine our answers to have the simplified version of the equation  .
.
To simplify a problem like the example above we must combine the like termed variables.
Like terms are the numbers that have the same variable, in this example, and
.
Separate the s to get
Then perform the necessary addition to get
Then separate the ’s to get
Then perform the necessary subtraction to get
We then combine our answers to have the simplified version of the equation 
Compare your answer with the correct one above
If  , what is
, what is  ?
?
If 

Let's start with our equation,  .
.
Subtract  from both sides:
from both sides:

Combine our  s:
s:

Divide both sides by  :
:

However, the problem is asking for  not
not  , so multiply both sides by
, so multiply both sides by  :
:

Let's start with our equation, 
Subtract 
Combine our 
Divide both sides by 
However, the problem is asking for 


Compare your answer with the correct one above
Simplify the following equation by combining like terms: 
Simplify the following equation by combining like terms:
X is the only term that appears twice in the equation. Since both are positive numbers, we can add the X terms to simplify the equation.

X is the only term that appears twice in the equation. Since both are positive numbers, we can add the X terms to simplify the equation.
Compare your answer with the correct one above
Combine the like terms for  .
.
Combine the like terms for 
Remember, adding a negative number is the same as subtracting a positive number. That means we can think of this problem as  .
.
If we think of this on a number line, we start at  , move left three units because of the
, move left three units because of the  , then move left again by one more unit for the
, then move left again by one more unit for the  , giving us a total of
, giving us a total of  .
.
Remember, adding a negative number is the same as subtracting a positive number. That means we can think of this problem as 
If we think of this on a number line, we start at 



Compare your answer with the correct one above
Simplify: 
Simplify:
Here, we are interested in combining like terms. Like terms are those with the same variable,.
When combining terms with  in them, we add the coefficients. Thus, we have
in them, we add the coefficients. Thus, we have  , and
, and  .
.
Therefore, we have  .
.
Here, we are interested in combining like terms. Like terms are those with the same variable,.
When combining terms with 


Therefore, we have 
Compare your answer with the correct one above
Which of the following numbers is the greatest?
Which of the following numbers is the greatest?
When comparing negative numbers, it is important to remember that the numbers with the larger absolute value (greatest numerical term) are actually more negative. Though it seems that  would be the largest number in this case, it is actually the smallest, as it is the farthest down the number line in the negative direction. The greatest number is the one with the smallest absolute value, which is
would be the largest number in this case, it is actually the smallest, as it is the farthest down the number line in the negative direction. The greatest number is the one with the smallest absolute value, which is  .
.
Remember, also, that zero is greater than any negative number!
When comparing negative numbers, it is important to remember that the numbers with the larger absolute value (greatest numerical term) are actually more negative. Though it seems that 

Remember, also, that zero is greater than any negative number!
Compare your answer with the correct one above
Place in order from smallest to largest:

Place in order from smallest to largest:
Find the least common denominator (LCD) and convert all fractions to the LCD. Then order the numerators from the smallest to the largest





So the correct order from smallest to largest is

Find the least common denominator (LCD) and convert all fractions to the LCD. Then order the numerators from the smallest to the largest
So the correct order from smallest to largest is
Compare your answer with the correct one above
Given that  is an odd integer, which of the following must produce an even integer?
is an odd integer, which of the following must produce an even integer?
Given that 
An easy way to solve this problem is to define  as 1, which is an odd integer. Plugging in 1 into each answer yields
as 1, which is an odd integer. Plugging in 1 into each answer yields  as the correct answer, since
as the correct answer, since 
4 is an even integer, which is what we are looking for.
An easy way to solve this problem is to define 

4 is an even integer, which is what we are looking for.
Compare your answer with the correct one above
Which number is greater?
 or
or 
Which number is greater?

When comparing negative numbers, recall the number line. Numbers that are "more negative", or negative with a large absolute value, are really very small. Thus, comparing negative numbers can sometimes seem counterintuitive. In this case, since we are comparing two negative numbers, the number with the larger absolute value is actually the smaller number. Therefore, the greater number is  .
.
When comparing negative numbers, recall the number line. Numbers that are "more negative", or negative with a large absolute value, are really very small. Thus, comparing negative numbers can sometimes seem counterintuitive. In this case, since we are comparing two negative numbers, the number with the larger absolute value is actually the smaller number. Therefore, the greater number is 
Compare your answer with the correct one above
Which of  and
and  is larger?
is larger?
Which of 

Recall that when comparing negative numbers, those numbers that are "more negative" are actually further to the left on the number line and thus are smaller. Therefore, even though  , we have that
, we have that  .
.
Therefore  is larger.
is larger.
Recall that when comparing negative numbers, those numbers that are "more negative" are actually further to the left on the number line and thus are smaller. Therefore, even though 

Therefore 
Compare your answer with the correct one above