Quadrilaterals - High School Math
Card 0 of 20
In the parallellogram, what is the value of 
?
In the parallellogram, what is the value of
Opposite angles are equal, and adjacent angles must sum to 180.
Therefore, we can set up an equation to solve for z:
(z – 15) + 2z = 180
3z - 15 = 180
3z = 195
z = 65
Now solve for x:
2_z_ = x = 130°
Opposite angles are equal, and adjacent angles must sum to 180.
Therefore, we can set up an equation to solve for z:
(z – 15) + 2z = 180
3z - 15 = 180
3z = 195
z = 65
Now solve for x:
2_z_ = x = 130°
Compare your answer with the correct one above
Find the measure of angle 
in the isosceles trapezoid pictured below.
Find the measure of angle
The sum of the angles in any quadrilateral is 360**°, and the properties of an isosceles trapezoid dictate that the sets of angles adjoined by parallel lines (in this case, the bottom set and top set of angles) are equal. Subtracting 2(72°) from 360°** gives the sum of the two top angles, and dividing the resulting 216**°** by 2 yields the measurement of x, which is 108**°**.
The sum of the angles in any quadrilateral is 360**°, and the properties of an isosceles trapezoid dictate that the sets of angles adjoined by parallel lines (in this case, the bottom set and top set of angles) are equal. Subtracting 2(72°) from 360°** gives the sum of the two top angles, and dividing the resulting 216**°** by 2 yields the measurement of x, which is 108**°**.
Compare your answer with the correct one above
Quadrilateral ABCD contains four ninety-degree angles. Which of the following must be true?
I. Quadrilateral ABCD is a rectangle.
II. Quadrilateral ABCD is a rhombus.
III. Quadrilateral ABCD is a square.
Quadrilateral ABCD contains four ninety-degree angles. Which of the following must be true?
I. Quadrilateral ABCD is a rectangle.
II. Quadrilateral ABCD is a rhombus.
III. Quadrilateral ABCD is a square.
Quadrilateral ABCD has four ninety-degree angles, which means that it has four right angles because every right angle measures ninety degrees. If a quadrilateral has four right angles, then it must be a rectangle by the definition of a rectangle. This means statement I is definitely true.
However, just because ABCD has four right angles doesn't mean that it is a rhombus. In order for a quadrilateral to be considered a rhombus, it must have four congruent sides. It's possible to have a rectangle whose sides are not all congruent. For example, if a rectangle has a width of 4 meters and a length of 8 meters, then not all of the sides of the rectangle would be congruent. In fact, in a rectangle, only opposite sides need be congruent. This means that ABCD is not necessarily a rhombus, and statement II does not have to be true.
A square is defined as a rhombus with four right angles. In a square, all of the sides must be congruent. In other words, a square is both a rectangle and a rhombus. However, we already established that ABCD doesn't have to be a rhombus. This means that ABCD need not be a square, because, as we said previously, not all of its sides must be congruent. Therefore, statement III isn't necessarily true either.
The only statement that has to be true is statement I.
The answer is I only.
Quadrilateral ABCD has four ninety-degree angles, which means that it has four right angles because every right angle measures ninety degrees. If a quadrilateral has four right angles, then it must be a rectangle by the definition of a rectangle. This means statement I is definitely true.
However, just because ABCD has four right angles doesn't mean that it is a rhombus. In order for a quadrilateral to be considered a rhombus, it must have four congruent sides. It's possible to have a rectangle whose sides are not all congruent. For example, if a rectangle has a width of 4 meters and a length of 8 meters, then not all of the sides of the rectangle would be congruent. In fact, in a rectangle, only opposite sides need be congruent. This means that ABCD is not necessarily a rhombus, and statement II does not have to be true.
A square is defined as a rhombus with four right angles. In a square, all of the sides must be congruent. In other words, a square is both a rectangle and a rhombus. However, we already established that ABCD doesn't have to be a rhombus. This means that ABCD need not be a square, because, as we said previously, not all of its sides must be congruent. Therefore, statement III isn't necessarily true either.
The only statement that has to be true is statement I.
The answer is I only.
Compare your answer with the correct one above
A quadrilateral with congruent sides is a __________.
A quadrilateral with congruent sides is a __________.
A rhombus is any quadrilateral with four congruent sides. A square is a quadrilateral with four congruent sides and four right angles. A square is also a rhombus.
Rectangles will have two pairs of congruent sides, but not all four sides will be congruent.
A rhombus is any quadrilateral with four congruent sides. A square is a quadrilateral with four congruent sides and four right angles. A square is also a rhombus.
Rectangles will have two pairs of congruent sides, but not all four sides will be congruent.
Compare your answer with the correct one above
Two rectangles are similar. The perimeter of the first rectangle is 36. The perimeter of the second is 12. If the base length of the second rectangle is 4, what is the height of the first rectangle?
Two rectangles are similar. The perimeter of the first rectangle is 36. The perimeter of the second is 12. If the base length of the second rectangle is 4, what is the height of the first rectangle?
Solve for the height of the second rectangle.
Perimeter = 2B + 2H
12 = 2(4) + 2H
12 = 8 + 2H
4 = 2H
H = 2
If they are similar, then the base and height are proportionally equal.
B1/H1 = B2/H2
4/2 = B2/H2
2 = B2/H2
B2 = 2H2
Use perimeter equation then solve for H:
Perimeter = 2B + 2H
36 = 2 B2 + 2 H2
36 = 2 (2H2) + 2 H2
36 = 4H2 + 2 H2
36 = 6H2
H2 = 6
Solve for the height of the second rectangle.
Perimeter = 2B + 2H
12 = 2(4) + 2H
12 = 8 + 2H
4 = 2H
H = 2
If they are similar, then the base and height are proportionally equal.
B1/H1 = B2/H2
4/2 = B2/H2
2 = B2/H2
B2 = 2H2
Use perimeter equation then solve for H:
Perimeter = 2B + 2H
36 = 2 B2 + 2 H2
36 = 2 (2H2) + 2 H2
36 = 4H2 + 2 H2
36 = 6H2
H2 = 6
Compare your answer with the correct one above
A quadrilateral ABCD has diagonals that are perpendicular bisectors of one another. Which of the following classifications must apply to quadrilateral ABCD?
I. parallelogram
II. rhombus
III. square
A quadrilateral ABCD has diagonals that are perpendicular bisectors of one another. Which of the following classifications must apply to quadrilateral ABCD?
I. parallelogram
II. rhombus
III. square
If the diagonals of a quadrilateral are perpendicular bisectors of one another, then the quadrilateral must be a rhombus, but not necessarily a square. Since all rhombi are also parallelograms, quadrilateral ABCD must be both a rhombus and parallelogram.
If the diagonals of a quadrilateral are perpendicular bisectors of one another, then the quadrilateral must be a rhombus, but not necessarily a square. Since all rhombi are also parallelograms, quadrilateral ABCD must be both a rhombus and parallelogram.
Compare your answer with the correct one above
What is the area of a kite with diagonals of 5 and 7?
What is the area of a kite with diagonals of 5 and 7?
To find the area of a kite using diagonals you use the following equation 
That diagonals (
and 
)are the lines created by connecting the two sides opposite of each other.
Plug in the diagonals for 
and 
to get 
Then multiply and divide to get the area. 
The answer is 
To find the area of a kite using diagonals you use the following equation
That diagonals (
Plug in the diagonals for
Then multiply and divide to get the area.
The answer is
Compare your answer with the correct one above
Find the area of the following kite:
Find the area of the following kite:
The formula for the area of a kite is:
Where 
is the length of one diagonal and 
is the length of the other diagonal
Plugging in our values, we get:
The formula for the area of a kite is:
Where
Plugging in our values, we get:
Compare your answer with the correct one above
Find the area of the following kite:
Find the area of the following kite:
The formula for the area of a kite is:
where 
is the length of one diagonal and 
is the length of another diagonal.
Use the formulas for a 
triangle and a 
triangle to find the lengths of the diagonals. The formula for a 
triangle is 
and the formula for a 
triangle is 
.
Our 
triangle is: 
Our 
triangle is: 
Plugging in our values, we get:
The formula for the area of a kite is:
where
Use the formulas for a
Our
Our
Plugging in our values, we get:
Compare your answer with the correct one above
What is the area of a parallelogram with a base of 
and a height of 
?
What is the area of a parallelogram with a base of
To solve this question you must know the formula for the area of a parallelogram.
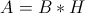
In this equation, 
is the length of the base and 
is the length of the height. We can plug in the side length for both base and height, as given in the question.
To solve this question you must know the formula for the area of a parallelogram.
In this equation,
Compare your answer with the correct one above
What is the area of a parallelogram with a base of 
and a height of 
?
What is the area of a parallelogram with a base of
To solve this question you must know the formula for the area of a parallelogram.
The formula is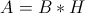
So we can plug in the side length for both base and height to yield 
Perform the multiplication to arrive at the answer of 
.
To solve this question you must know the formula for the area of a parallelogram.
The formula is
So we can plug in the side length for both base and height to yield
Perform the multiplication to arrive at the answer of
Compare your answer with the correct one above
Find the area of the following parallelogram:
Find the area of the following parallelogram:
The formula for the area of a parallelogram is:
,
where 
is the length of the base and 
is the length of the height.
In order to the find the height of the parallelogram, use the formula for a 
triangle:
, where 
is the side opposite the 
.
The left side of the parallelogram forms the following triangle:
, where 
is the length of the height.
Plugging in our values, we get:
The formula for the area of a parallelogram is:
where
In order to the find the height of the parallelogram, use the formula for a
The left side of the parallelogram forms the following
Plugging in our values, we get:
Compare your answer with the correct one above
Find the area of the following parallelogram:
Find the area of the following parallelogram:
Use the Pythagorean Theorem to determine the length of the diagonal:
The area of the parallelogram is twice the area of the right triangles:
Use the Pythagorean Theorem to determine the length of the diagonal:
The area of the parallelogram is twice the area of the right triangles:
Compare your answer with the correct one above
Find the area of the following parallelogram:
Find the area of the following parallelogram:
The formula for the area of a parallelogram is
.
Use the formula for a 
triangle to find the length of the height:
Plugging in our values, we get:
The formula for the area of a parallelogram is
Use the formula for a
Plugging in our values, we get:
Compare your answer with the correct one above
Mark is making a plan to build a rectangular garden. He has 160 feet of fence to form the outside border of the garden. He wants the dimensions to look like the plan outlined below:
What is the area of the garden, rounded to the nearest square foot?
Mark is making a plan to build a rectangular garden. He has 160 feet of fence to form the outside border of the garden. He wants the dimensions to look like the plan outlined below:
What is the area of the garden, rounded to the nearest square foot?
Perimeter: Sum of the sides:
4x + 4x + 2x+8 +2x+8 = 160
12x + 6 = 160
12x = 154
x = 
Therefore, the short side of the rectangle is going to be:
And the long side is going to be:
The area of the rectangle is going to be as follows:
Area = lw
Perimeter: Sum of the sides:
4x + 4x + 2x+8 +2x+8 = 160
12x + 6 = 160
12x = 154
x =
Therefore, the short side of the rectangle is going to be:
And the long side is going to be:
The area of the rectangle is going to be as follows:
Area = lw
Compare your answer with the correct one above
Erin is getting ready to plant her tulip garden. She wants to plant two tulips per square foot of garden. If her rectangular garden is enclosed by 24 feet of fencing, and the length of the fence is twice as long as its width, how many tulips will Erin plant?
Erin is getting ready to plant her tulip garden. She wants to plant two tulips per square foot of garden. If her rectangular garden is enclosed by 24 feet of fencing, and the length of the fence is twice as long as its width, how many tulips will Erin plant?
We know that the following represents the formula for the perimeter of a rectangle:
In this particular case, we are told that the length of the fence is twice as long as the width. We can write this as the following expression:
Use this information to substitute in a variable for the length that matches the variable for width in our perimeter equation.
We also know that the length is two times the width; therefore, we can write the following:
The area of a rectangle is found by using this formula:
The area of the garden is 32 square feet. Erin will plant two tulips per square foot; thus, she will plant 64 tulips.
We know that the following represents the formula for the perimeter of a rectangle:
In this particular case, we are told that the length of the fence is twice as long as the width. We can write this as the following expression:
Use this information to substitute in a variable for the length that matches the variable for width in our perimeter equation.
We also know that the length is two times the width; therefore, we can write the following:
The area of a rectangle is found by using this formula:
The area of the garden is 32 square feet. Erin will plant two tulips per square foot; thus, she will plant 64 tulips.
Compare your answer with the correct one above
A contractor is going to re-tile a rectangular section of the kitchen floor. If the floor is 6ft x 3ft, and he is going to use square tiles with a side of 9in. How many tiles will be needed?
A contractor is going to re-tile a rectangular section of the kitchen floor. If the floor is 6ft x 3ft, and he is going to use square tiles with a side of 9in. How many tiles will be needed?
We have to be careful of our units. The floor is given in feet and the tile in inches. Since the floor is 6ft x 3ft. we can say it is 72in x 36in, because 12 inches equals 1 foot. If the tiles are 9in x 9in we can fit 8 tiles along the length and 4 tiles along the width. To find the total number of tiles we multiply 8 x 4 = 32. Alternately we could find the area of the floor (72 x 36, and divide by the area of the tile 9 x 9)
We have to be careful of our units. The floor is given in feet and the tile in inches. Since the floor is 6ft x 3ft. we can say it is 72in x 36in, because 12 inches equals 1 foot. If the tiles are 9in x 9in we can fit 8 tiles along the length and 4 tiles along the width. To find the total number of tiles we multiply 8 x 4 = 32. Alternately we could find the area of the floor (72 x 36, and divide by the area of the tile 9 x 9)
Compare your answer with the correct one above
A rectangle has a perimeter of 40 inches. It is 3 times as long as it is wide. What is the area of the rectangle in square inches?
A rectangle has a perimeter of 40 inches. It is 3 times as long as it is wide. What is the area of the rectangle in square inches?
The width of the rectangle is w, therefore the length is 3w. The perimeter, P, can then be described as P = w + w + 3w +3w
40 = 8w
w = 5
width = 5, length = 3w = 15
A = 5*15 = 75 square inches
The width of the rectangle is w, therefore the length is 3w. The perimeter, P, can then be described as P = w + w + 3w +3w
40 = 8w
w = 5
width = 5, length = 3w = 15
A = 5*15 = 75 square inches
Compare your answer with the correct one above
Angela is carpeting a rectangular conference room that measures 20 feet by 30 feet. If carpet comes in rectangular pieces that measures 5 feet by 4 feet, how many carpet pieces will she need to carpet the entire room?
Angela is carpeting a rectangular conference room that measures 20 feet by 30 feet. If carpet comes in rectangular pieces that measures 5 feet by 4 feet, how many carpet pieces will she need to carpet the entire room?
First, we need to find the area of the room. Because the room is rectangular, we can multiply 20 feet by 30 feet, which is 600 square feet. Next, we need to know how much space one carpet piece covers. Because the carpet pieces are also rectangular, we can multiply 4 feet by 5 feet to get 20 feet. To determine how many pieces of carpet Angela will need, we must divide the total square footage of the room (600 feet) by the square footage covered by one carpet piece (20 feet). 600 divided by 20 is 30, so Angela will need 30 carpet pieces to carpet the entire room.
First, we need to find the area of the room. Because the room is rectangular, we can multiply 20 feet by 30 feet, which is 600 square feet. Next, we need to know how much space one carpet piece covers. Because the carpet pieces are also rectangular, we can multiply 4 feet by 5 feet to get 20 feet. To determine how many pieces of carpet Angela will need, we must divide the total square footage of the room (600 feet) by the square footage covered by one carpet piece (20 feet). 600 divided by 20 is 30, so Angela will need 30 carpet pieces to carpet the entire room.
Compare your answer with the correct one above
If the area Rectangle A is 
larger than Rectangle B and the sides of Rectangle A are 
and 
, what is the area of Rectangle B?
If the area Rectangle A is
Compare your answer with the correct one above