Lines - High School Math

Card 0 of 17

Question

If $\overleftrightarrow{FH} \parallel \overleftrightarrow{AD}$ , $\overline{BE}\perp \overleftrightarrow{GC}$ , and $m\angle HGC=58^\circ$ , what is the measure, in degrees, of $\angle ABE$ ?

Answer

The question states that $\overleftrightarrow{FH} \parallel \overleftrightarrow{AD}$ . The alternate interior angle theorem states that if two parallel lines are cut by a transversal, then pairs of alternate interior angles are congruent; therefore, we know the following measure:

$m\angle GCA = 58^\circ$

The sum of angles of a triangle is equal to 180 degrees. The question states that $\overline{BE}\perp \overleftrightarrow{GC}$ ; therefore we know the following measure:

$m \angle BEC = 90^\circ$

Use this information to solve for the missing angle: $\angle EBC$

$180^\circ=m\angle EBC+58^\circ+90^\circ$

$m\angle EBC=32^\circ$

The degree measure of a straight line is 180 degrees; therefore, we can write the following equation:

$180^\circ=m\angle ABE+32^\circ$

$m\angle ABE=148^\circ$

The measure of $\angle ABE$ is 148 degrees.

Compare your answer with the correct one above

Question

In the following diagram, lines and are parallel to each other. What is the value for ?

Answer

When two parallel lines are intersected by another line, the sum of the measures of the interior angles on the same side of the line is 180°. Therefore, the sum of the angle that is labeled as 100° and angle y is 180°. As a result, angle y is 80°.

Another property of two parallel lines that are intersected by a third line is that the corresponding angles are congruent. So, the measurement of angle x is equal to the measurement of angle y, which is 80°.

Compare your answer with the correct one above

Question

Two pairs of parallel lines intersect:

If A = 135o, what is 2*|B-C| = ?

Answer

By properties of parallel lines A+B = 180o, B = 45o, C = A = 135o, so 2|B-C| = 2 |45-135| = 180o

Compare your answer with the correct one above

Question

Lines A and B in the diagram below are parallel. The triangle at the bottom of the figure is an isosceles triangle.

What is the degree measure of angle ?

Answer

Since A and B are parallel, and the triangle is isosceles, we can use the supplementary rule for the two angles, and which will sum up to . Setting up an algebraic equation for this, we get . Solving for , we get . With this, we can get either (for the smaller angle) or (for the larger angle - must then use supplementary rule again for inner smaller angle). Either way, we find that the inner angles at the top are 80 degrees each. Since the sum of the angles within a triangle must equal 180, we can set up the equation as

degrees.

Compare your answer with the correct one above

Question

Figure not drawn to scale.

In the figure above, APB forms a straight line. If the measure of angle APC is eighty-one degrees larger than the measure of angle DPB, and the measures of angles CPD and DPB are equal, then what is the measure, in degrees, of angle CPB?

Answer

Let x equal the measure of angle DPB. Because the measure of angle APC is eighty-one degrees larger than the measure of DPB, we can represent this angle's measure as x + 81. Also, because the measure of angle CPD is equal to the measure of angle DPB, we can represent the measure of CPD as x.

Since APB is a straight line, the sum of the measures of angles DPB, APC, and CPD must all equal 180; therefore, we can write the following equation to find x:

x + (x + 81) + x = 180

Simplify by collecting the x terms.

3x + 81 = 180

Subtract 81 from both sides.

3x = 99

Divide by 3.

x = 33.

This means that the measures of angles DPB and CPD are both equal to 33 degrees. The original question asks us to find the measure of angle CPB, which is equal to the sum of the measures of angles DPB and CPD.

measure of CPB = 33 + 33 = 66.

The answer is 66.

Compare your answer with the correct one above

Question

One-half of the measure of the supplement of angle ABC is equal to the twice the measure of angle ABC. What is the measure, in degrees, of the complement of angle ABC?

Answer

Let x equal the measure of angle ABC, let y equal the measure of the supplement of angle ABC, and let z equal the measure of the complement of angle ABC.

Because x and y are supplements, the sum of their measures must equal 180. In other words, x + y = 180.

We are told that one-half of the measure of the supplement is equal to twice the measure of ABC. We could write this equation as follows:

(1/2)y = 2x.

Because x + y = 180, we can solve for y in terms of x by subtracting x from both sides. In other words, y = 180 – x. Next, we can substitute this value into the equation (1/2)y = 2x and then solve for x.

(1/2)(180-x) = 2x.

Multiply both sides by 2 to get rid of the fraction.

(180 – x) = 4x.

Add x to both sides.

180 = 5x.

Divide both sides by 5.

x = 36.

The measure of angle ABC is 36 degrees. However, the original question asks us to find the measure of the complement of ABC, which we denoted previously as z. Because the sum of the measure of an angle and the measure of its complement equals 90, we can write the following equation:

x + z = 90.

Now, we can substitute 36 as the value of x and then solve for z.

36 + z = 90.

Subtract 36 from both sides.

z = 54.

The answer is 54.

Compare your answer with the correct one above

Question

In the diagram, AB || CD. What is the value of a+b?

Answer

Refer to the following diagram while reading the explanation:

We know that angle b has to be equal to its vertical angle (the angle directly "across" the intersection). Therefore, it is 20°.

Furthermore, given the properties of parallel lines, we know that the supplementary angle to a must be 40°. Based on the rule for supplements, we know that a + 40° = 180°. Solving for a, we get a = 140°.

Therefore, a + b = 140° + 20° = 160°

Compare your answer with the correct one above

Question

The measure of the supplement of angle A is 40 degrees larger than twice the measure of the complement of angle A. What is the sum, in degrees, of the measures of the supplement and complement of angle A?

Answer

Let A represent the measure, in degrees, of angle A. By definition, the sum of the measures of A and its complement is 90 degrees. We can write the following equation to determine an expression for the measure of the complement of angle A.

A + measure of complement of A = 90

Subtract A from both sides.

measure of complement of A = 90 – A

Similarly, because the sum of the measures of angle A and its supplement is 180 degrees, we can represent the measure of the supplement of A as 180 – A.

The problem states that the measure of the supplement of A is 40 degrees larger than twice the measure of the complement of A. We can write this as 2(90-A) + 40.

Next, we must set the two expressions 180 – A and 2(90 – A) + 40 equal to one another and solve for A:

180 – A = 2(90 – A) + 40

Distribute the 2:

180 - A = 180 – 2A + 40

Add 2A to both sides:

180 + A = 180 + 40

Subtract 180 from both sides:

A = 40

Therefore the measure of angle A is 40 degrees.

The question asks us to find the sum of the measures of the supplement and complement of A. The measure of the supplement of A is 180 – A = 180 – 40 = 140 degrees. Similarly, the measure of the complement of A is 90 – 40 = 50 degrees.

The sum of these two is 140 + 50 = 190 degrees.

Compare your answer with the correct one above

Question

In rectangle ABCD, both diagonals are drawn and intersect at point E.

Let the measure of angle AEB equal x degrees.

Let the measure of angle BEC equal y degrees.

Let the measure of angle CED equal z degrees.

Find the measure of angle AED in terms of x, y, and/or z.

Answer

Intersecting lines create two pairs of vertical angles which are congruent. Therefore, we can deduce that y = measure of angle AED.

Furthermore, intersecting lines create adjacent angles that are supplementary (sum to 180 degrees). Therefore, we can deduce that x + y + z + (measure of angle AED) = 360.

Substituting the first equation into the second equation, we get

x + (measure of angle AED) + z + (measure of angle AED) = 360

2(measure of angle AED) + x + z = 360

2(measure of angle AED) = 360 – (x + z)

Divide by two and get:

measure of angle AED = 180 – 1/2(x + z)

Compare your answer with the correct one above

Question

$\dpi{100} \small \overline{AB}$ is a straight line. $\dpi{100} \small \overline{CD}$ intersects $\dpi{100} \small \overline{AB}$ at point $\dpi{100} \small E$ . If $\dpi{100} \small \angle AEC$ measures 120 degrees, what must be the measure of $\dpi{100} \small \angle BEC$ ?

Answer

$\dpi{100} \small \angle AEC$ & $\dpi{100} \small \angle BEC$ must add up to 180 degrees. So, if $\dpi{100} \small \angle AEC$ is 120, $\dpi{100} \small \angle BEC$ (the supplementary angle) must equal 60, for a total of 180.

Compare your answer with the correct one above

Question

If $\angle A$ measures $(40-10x)^{\circ}$ , which of the following is equivalent to the measure of the supplement of $\angle A$ ?

Answer

When the measure of an angle is added to the measure of its supplement, the result is always 180 degrees. Put differently, two angles are said to be supplementary if the sum of their measures is 180 degrees. For example, two angles whose measures are 50 degrees and 130 degrees are supplementary, because the sum of 50 and 130 degrees is 180 degrees. We can thus write the following equation:

$\dpi{100} measure\ of\ \angle A+ measure\ of\ supplement\ of\ \angle A=180$

$\dpi{100} 40-10x+ measure\ of\ supplement\ of\ \angle A=180$

Subtract 40 from both sides.

$\dpi{100} -10x+ measure\ of\ supplement\ of\ \angle A=140$

Add $\dpi{100} 10x$ to both sides.

$\dpi{100} measure\ of\ supplement\ of\ \angle A=140+10x=10x+140$

The answer is $(10x+140)^{\circ}$ .

Compare your answer with the correct one above

Question

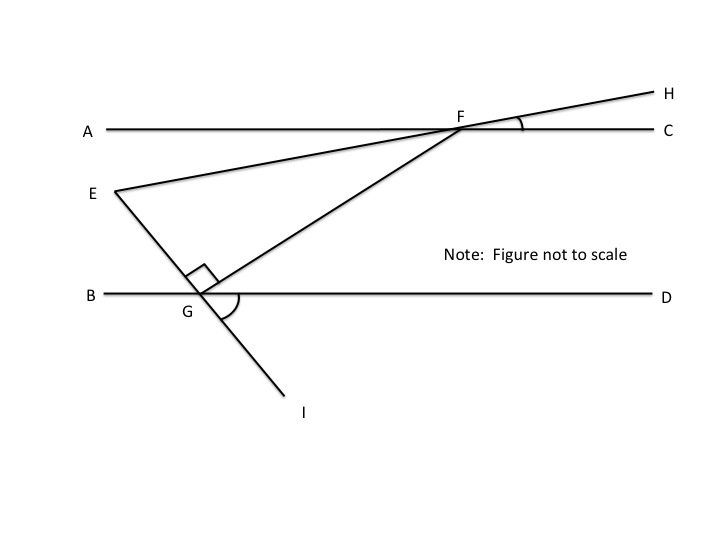
Lines and are parallel. $\angle HFC=10^{\circ}$ , $\angle DGI=50^{\circ}$ , $\triangle EFG$ is a right triangle, and $\overline{EG}$ has a length of 10. What is the length of $\overline{EF}$

Answer

Since we know opposite angles are equal, it follows that angle $\angle AFE=10^{\circ}$ and $\angle BGE=50^{\circ}$ .

Imagine a parallel line passing through point . The imaginary line would make opposite angles with $\angle AFE$ & $\angle BGE$ , the sum of which would equal $\angle FEG$ . Therefore, $\angle FEG=60^{\circ}$ .

$\cos (60)=.5=\frac{EG}{EF}\rightarrow EF=\frac{EG}{.5}=20$

Compare your answer with the correct one above

Question

Two angles are supplementary and have a ratio of 1:4. What is the size of the smaller angle?

Answer

Since the angles are supplementary, their sum is 180 degrees. Because they are in a ratio of 1:4, the following expression could be written:

$x+4x=180$

$5x=180$

$x=36^{\circ}$

Compare your answer with the correct one above

Question

Lines and are parallel. Which angle is congruent to angle ?

Answer

When two lines are parallel, corresponding angles are congruent. Because we don't know if lines and are parallel, we can't make any conclusions about angles 2 and 3.

With the given information, we can ignore line , as it has no relation to angle . This leaves angles 1 and 4 as possible answers. Angle 4 will be congruent to angle , while angle 1 will supplement angle .

Compare your answer with the correct one above

Question

and are parallel lines. Solve for .

Figure not drawn to scale.

Answer

The angles are alternate exterior angles and are, therefore, equal.

$\small 6x-8=2x+20$

$\small 6x=2x+28$

$\small 4x=28$

$\small x=7$

Compare your answer with the correct one above

Question

Give another name for $\angle AVC$ .

Answer

Since the angle is called $\angle AVC$ , it has vertex - the middle letter is always the vertex - and it is the union of rays $\overrightarrow{VA}$ and $\overrightarrow{VC}$ . Another name for $\overrightarrow{VC}$ is $\overrightarrow{VD}$ , since is also on that ray, so the angle can be said to be the union of $\overrightarrow{VA}$ and $\overrightarrow{VD}$ ; this makes $\angle DVA$ a valid name for the angle.

$\angle ACV$ and $\angle VAD$ are not valid, since the middle letter is not vertex . $\angle CVD$ is not valid, since and are on the same side of the angle. $\angle V$ is not valid; an angle can be named using only its vertex only if it is the only angle in the diagram with that vertex, and that is not the case here.

Compare your answer with the correct one above

Question

Lines $\small l$ and $\small m$ are parallel. Which of the following pairs of angles are supplementary?

Answer

Coresponding angles can be found when a line crosses two parallel lines. Angles 10 and 14 are equal, because corresponding angles are equal. Angles 14 and 13 are supplementary because together they form a straight line. If angles 10 and 14 are equal, then angles 10 and 13 must be supplementary as well.

Compare your answer with the correct one above

Tap the card to reveal the answer