How to find the surface area of a cone - High School Math
Card 0 of 8
The lateral area is twice as big as the base area of a cone. If the height of the cone is 9, what is the entire surface area (base area plus lateral area)?
The lateral area is twice as big as the base area of a cone. If the height of the cone is 9, what is the entire surface area (base area plus lateral area)?
Lateral Area = LA = π(r)(l) where r = radius of the base and l = slant height
LA = 2B
π(r)(l) = 2π(r2)
rl = 2r2
l = 2r

From the diagram, we can see that r2 + h2 = l2. Since h = 9 and l = 2r, some substitution yields
r2 + 92 = (2r)2
r2 + 81 = 4r2
81 = 3r2
27 = r2
B = π(r2) = 27π
LA = 2B = 2(27π) = 54π
SA = B + LA = 81π
Lateral Area = LA = π(r)(l) where r = radius of the base and l = slant height
LA = 2B
π(r)(l) = 2π(r2)
rl = 2r2
l = 2r

From the diagram, we can see that r2 + h2 = l2. Since h = 9 and l = 2r, some substitution yields
r2 + 92 = (2r)2
r2 + 81 = 4r2
81 = 3r2
27 = r2
B = π(r2) = 27π
LA = 2B = 2(27π) = 54π
SA = B + LA = 81π
Compare your answer with the correct one above
What is the surface area of a cone with a radius of 6 in and a height of 8 in?
What is the surface area of a cone with a radius of 6 in and a height of 8 in?
Find the slant height of the cone using the Pythagorean theorem: _r_2 + _h_2 = _s_2 resulting in 62 + 82 = _s_2 leading to _s_2 = 100 or s = 10 in
SA = πrs + πr_2 = π(6)(10) + π(6)2 = 60_π + 36_π_ = 96_π_ in2
60_π_ in2 is the area of the cone without the base.
36_π_ in2 is the area of the base only.
Find the slant height of the cone using the Pythagorean theorem: _r_2 + _h_2 = _s_2 resulting in 62 + 82 = _s_2 leading to _s_2 = 100 or s = 10 in
SA = πrs + πr_2 = π(6)(10) + π(6)2 = 60_π + 36_π_ = 96_π_ in2
60_π_ in2 is the area of the cone without the base.
36_π_ in2 is the area of the base only.
Compare your answer with the correct one above
What is the surface area of a cone with a radius of 4 and a height of 3?
What is the surface area of a cone with a radius of 4 and a height of 3?
Here we simply need to remember the formula for the surface area of a cone and plug in our values for the radius and height.

Here we simply need to remember the formula for the surface area of a cone and plug in our values for the radius and height.
Compare your answer with the correct one above
What is the surface area of a cone with a height of 8 and a base with a radius of 5?
What is the surface area of a cone with a height of 8 and a base with a radius of 5?
To find the surface area of a cone we must plug in the appropriate numbers into the equation

where  is the radius of the base, and
is the radius of the base, and  is the lateral, or slant height of the cone.
is the lateral, or slant height of the cone.
First we must find the area of the circle.
To find the area of the circle we plug in our radius into the equation of a circle which is 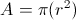
This yields  .
.
We then need to know the surface area of the cone shape.
To find this we must use our height and our radius to make a right triangle in order to find the lateral height using Pythagorean’s Theorem.
Pythagorean’s Theorem states 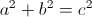
Take the radius and height and plug them into the equation as a and b to yield 
First square the numbers 
After squaring the numbers add them together 
Once you have the sum, square root both sides 
After calculating we find our length is 
Then plug the length into the second portion of our surface area equation above to get 
Then add the area of the circle with the conical area to find the surface area of the entire figure 
The answer is  .
.
To find the surface area of a cone we must plug in the appropriate numbers into the equation
where 

First we must find the area of the circle.
To find the area of the circle we plug in our radius into the equation of a circle which is
This yields 
We then need to know the surface area of the cone shape.
To find this we must use our height and our radius to make a right triangle in order to find the lateral height using Pythagorean’s Theorem.
Pythagorean’s Theorem states
Take the radius and height and plug them into the equation as a and b to yield
First square the numbers
After squaring the numbers add them together
Once you have the sum, square root both sides
After calculating we find our length is
Then plug the length into the second portion of our surface area equation above to get
Then add the area of the circle with the conical area to find the surface area of the entire figure
The answer is 
Compare your answer with the correct one above
Find the surface area of a cone that has a radius of 12 and a slant height of 15.
Find the surface area of a cone that has a radius of 12 and a slant height of 15.
The standard equation to find the surface area of a cone is

where  denotes the slant height of the cone, and
denotes the slant height of the cone, and  denotes the radius.
denotes the radius.
Plug in the given values for  and
and  to find the answer:
to find the answer:

The standard equation to find the surface area of a cone is
where 

Plug in the given values for 

Compare your answer with the correct one above
Find the surface area of the following cone.

Find the surface area of the following cone.

The formula for the surface area of a cone is:


where  is the radius of the cone and
is the radius of the cone and  is the slant height of the cone.
is the slant height of the cone.
Plugging in our values, we get:


The formula for the surface area of a cone is:
where 

Plugging in our values, we get:
Compare your answer with the correct one above
Find the surface area of the following cone.

Find the surface area of the following cone.

The formula for the surface area of a cone is:



Use the Pythagorean Theorem to find the length of the radius:



Plugging in our values, we get:


The formula for the surface area of a cone is:
Use the Pythagorean Theorem to find the length of the radius:
Plugging in our values, we get:
Compare your answer with the correct one above
Find the surface area of the following half cone.

Find the surface area of the following half cone.

The formula for the surface area of the half cone is:


Where  is the radius,
is the radius,  is the slant height, and
is the slant height, and  is the height of the cone.
is the height of the cone.
Use the Pythagorean Theorem to find the height of the cone:



Plugging in our values, we get:



The formula for the surface area of the half cone is:
Where 


Use the Pythagorean Theorem to find the height of the cone:
Plugging in our values, we get:
Compare your answer with the correct one above