How to find the length of the diagonal of a rectangle - High School Math
Card 0 of 3
The length and width of a rectangle are in the ratio of 3:4. If the rectangle has an area of 108 square centimeters, what is the length of the diagonal?
The length and width of a rectangle are in the ratio of 3:4. If the rectangle has an area of 108 square centimeters, what is the length of the diagonal?
The length and width of the rectangle are in a ratio of 3:4, so the sides can be written as 3_x_ and 4_x_.
We also know the area, so we write an equation and solve for x:
(3_x_)(4_x_) = 12_x_2 = 108.
x2 = 9
x = 3
Now we can recalculate the length and the width:
length = 3x = 3(3) = 9 centimeters
width = 4x = 4(3) = 12 centimeters
Using the Pythagorean Theorem we can find the diagonal, c:
length2 + width2 = c2
92 + 122 = _c_2
81 + 144 = c2
225 = c2
c = 15 centimeters
The length and width of the rectangle are in a ratio of 3:4, so the sides can be written as 3_x_ and 4_x_.
We also know the area, so we write an equation and solve for x:
(3_x_)(4_x_) = 12_x_2 = 108.
x2 = 9
x = 3
Now we can recalculate the length and the width:
length = 3x = 3(3) = 9 centimeters
width = 4x = 4(3) = 12 centimeters
Using the Pythagorean Theorem we can find the diagonal, c:
length2 + width2 = c2
92 + 122 = _c_2
81 + 144 = c2
225 = c2
c = 15 centimeters
Compare your answer with the correct one above
What is the length of the diagonal of a rectangle that is 3 feet long and 4 feet wide?
What is the length of the diagonal of a rectangle that is 3 feet long and 4 feet wide?
The diagonal of the rectangle is equivalent to finding the length of the hypotenuse of a right triangle with sides 3 and 4. Using the Pythagorean Theorem:
Therefore the diagonal of the rectangle is 5 feet.
The diagonal of the rectangle is equivalent to finding the length of the hypotenuse of a right triangle with sides 3 and 4. Using the Pythagorean Theorem:
Therefore the diagonal of the rectangle is 5 feet.
Compare your answer with the correct one above
What is the diagonal of a rectangle with a side length of 5 and a base of 8? (Round to the nearest tenth)
What is the diagonal of a rectangle with a side length of 5 and a base of 8? (Round to the nearest tenth)
To find the diagonal of a rectangle we must use the side lengths to create a 90 degree triangle with side lengths of 5, 8, and a hypotenuse which is equal to the diagonal.
If we have a right angle triangle and a value for two of the three side lengths, we use the Pythagorean Theorem to solve for the length of the third side.
The two side lengths that meet to form the right angle are labeled 
and 
which are interchangeable for each side length.
The long length connecting them is labeled 
and is known as the hypotenuse.
The Pythagorean Theorem states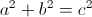 
Take 5 and 8 and plug them into the equation as 
and 
to yield 
First square the numbers 
After squaring the numbers add them together 
Once you have the sum, square root both sides 
After calculating our answer for the diagonal is 
.
To find the diagonal of a rectangle we must use the side lengths to create a 90 degree triangle with side lengths of 5, 8, and a hypotenuse which is equal to the diagonal.
If we have a right angle triangle and a value for two of the three side lengths, we use the Pythagorean Theorem to solve for the length of the third side.
The two side lengths that meet to form the right angle are labeled
The long length connecting them is labeled
The Pythagorean Theorem states
Take 5 and 8 and plug them into the equation as
First square the numbers
After squaring the numbers add them together
Once you have the sum, square root both sides
After calculating our answer for the diagonal is
Compare your answer with the correct one above