How to find the area of a polygon - High School Math
Card 0 of 10
What is the area of a regular heptagon with an apothem of 4 and a side length of 6?
What is the area of a regular heptagon with an apothem of 4 and a side length of 6?
What is the area of a regular heptagon with an apothem of 4 and a side length of 6?
To find the area of any polygon with the side length and the apothem we must know the equation for the area of a polygon which is
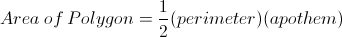
First, we must calculate the perimeter using the side length.
To find the perimeter of a regular polygon we take the length of each side and multiply it by the number of sides.
In a heptagon the number of sides is 7 and in this example the side length is 6 so 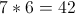
The perimeter is  .
.
Then we plug in the numbers for the apothem and perimeter into the equation yielding 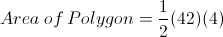
We then multiply giving us the area of 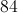 .
.
What is the area of a regular heptagon with an apothem of 4 and a side length of 6?
To find the area of any polygon with the side length and the apothem we must know the equation for the area of a polygon which is
First, we must calculate the perimeter using the side length.
To find the perimeter of a regular polygon we take the length of each side and multiply it by the number of sides.
In a heptagon the number of sides is 7 and in this example the side length is 6 so
The perimeter is .
Then we plug in the numbers for the apothem and perimeter into the equation yielding
We then multiply giving us the area of .
Compare your answer with the correct one above
What is the area of a regular decagon with an apothem of 15 and a side length of 25?
What is the area of a regular decagon with an apothem of 15 and a side length of 25?
To find the area of any polygon with the side length and the apothem we must know the equation for the area of a polygon which is
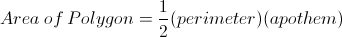
First, we must calculate the perimeter using the side length.
To find the perimeter of a regular polygon we take the length of each side and multiply it by the number of sides.
In a decagon the number of sides is 10 and in this example the side length is 25 so 
The perimeter is  .
.
Then we plug in the numbers for the apothem and perimeter into the equation yielding 
We then multiply giving us the area of  .
.
To find the area of any polygon with the side length and the apothem we must know the equation for the area of a polygon which is
First, we must calculate the perimeter using the side length.
To find the perimeter of a regular polygon we take the length of each side and multiply it by the number of sides.
In a decagon the number of sides is 10 and in this example the side length is 25 so
The perimeter is 
Then we plug in the numbers for the apothem and perimeter into the equation yielding
We then multiply giving us the area of 
Compare your answer with the correct one above
What is the area of a regular heptagon with an apothem of  and a side length of
and a side length of  ?
?
What is the area of a regular heptagon with an apothem of 

To find the area of any polygon with the side length and the apothem we must know the equation for the area of a polygon which is 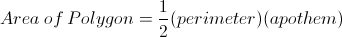
We must then calculate the perimeter using the side length.
To find the perimeter of a regular polygon we take the length of each side and multiply it by the number of sides  .
.
In a heptagon the number of sides  is
is  and in this example the side length is
and in this example the side length is  so
so 
The perimeter is 56.
Then we plug in the numbers for the apothem and perimeter into the equation yielding 
We then multiply giving us the area of  .
.
To find the area of any polygon with the side length and the apothem we must know the equation for the area of a polygon which is
We must then calculate the perimeter using the side length.
To find the perimeter of a regular polygon we take the length of each side and multiply it by the number of sides 
In a heptagon the number of sides 


The perimeter is 56.
Then we plug in the numbers for the apothem and perimeter into the equation yielding
We then multiply giving us the area of 
Compare your answer with the correct one above
Find the area of the shaded region:

Find the area of the shaded region:

To find the area of the shaded region, you must subtract the area of the circle from the area of the square.
The formula for the shaded area is:

 ,
,
where  is the side of the square and
is the side of the square and  is the radius of the circle.
is the radius of the circle.
Plugging in our values, we get:


To find the area of the shaded region, you must subtract the area of the circle from the area of the square.
The formula for the shaded area is:

where 

Plugging in our values, we get:
Compare your answer with the correct one above
Find the area of the shaded region:

Find the area of the shaded region:

To find the area of the shaded region, you need to subtract the area of the triangle from the area of the sector:


Where  is the radius of the circle,
is the radius of the circle,  is the fraction of the circle,
is the fraction of the circle,  is the base of the triangle, and
is the base of the triangle, and  is the height of the triangle
is the height of the triangle
Plugging in our values, we get


To find the area of the shaded region, you need to subtract the area of the triangle from the area of the sector:
Where 



Plugging in our values, we get
Compare your answer with the correct one above
Find the area of the shaded region:

Find the area of the shaded region:

To find the area of the shaded region, you need to subtract the area of the equilateral triangle from the area of the sector:


Where  is the radius of the circle,
is the radius of the circle,  is the fraction of the circle, and
is the fraction of the circle, and  is the side of the triangle
is the side of the triangle
Plugging in our values, we get


To find the area of the shaded region, you need to subtract the area of the equilateral triangle from the area of the sector:
Where 


Plugging in our values, we get
Compare your answer with the correct one above
Find the area of the shaded region:

Find the area of the shaded region:

The formula for the area of the shaded region is

where  is the radius of the circle.
is the radius of the circle.
Plugging in our values, we get:


The formula for the area of the shaded region is
where 
Plugging in our values, we get:
Compare your answer with the correct one above
Find the area of the following octagon:

Find the area of the following octagon:

The formula for the area of a regular octagon is:

Plugging in our values, we get:


The formula for the area of a regular octagon is:
Plugging in our values, we get:
Compare your answer with the correct one above
Find the area of a rectangle with a base of  and a width of
and a width of  in terms of
in terms of  .
.
Find the area of a rectangle with a base of 


This problem simply becomes a matter of FOILing (first outer inner last)
The area of the shape is Base times Height.
So, multiplying  and
and  using FOIL, we get an area of
using FOIL, we get an area of 
This problem simply becomes a matter of FOILing (first outer inner last)
The area of the shape is Base times Height.
So, multiplying 

Compare your answer with the correct one above
Find the area of a square whose diagonal is  .
.
Find the area of a square whose diagonal is 
If the diagonal of a square is  , we can use the pythagorean theorem to solve for the length of the sides.
, we can use the pythagorean theorem to solve for the length of the sides.
 = length of side of the square
= length of side of the square
Doing so, we get 

To find the area of the square, we square  , resulting in
, resulting in  .
.
If the diagonal of a square is 

Doing so, we get
To find the area of the square, we square 

Compare your answer with the correct one above