Solid Geometry - High School Math

Card 0 of 20

Question

Find the length of the diagonal connecting opposite corners of a cube with sides of length $2\sqrt{2}$ .

Answer

Find the diagonal of one face of the cube using the Pythagorean Theorem applied to a triangle formed by two sides of that face ( and ) and the diagonal itself ():

$(2\sqrt{2})^2 + (2\sqrt{2})^2 = c^2$

$\rightarrow 8 + 8 = c^2$

$\rightarrow 16 = c^2$

$\rightarrow c = 4$

This diagonal is now the base of a new right triangle (call this ). The height of that triangle is an edge of the cube that runs perpendicular to this diagonal (call this ). The third side of the triangle formed by and is a line from one corner of the cube to the other, i.e., the cube's diagonal (call this ). Use the Pythagorean Theorem again with the triangle formed by , , and to find the length of this diagonal.

$(2\sqrt{2})^2 + (4)^2 = c^2$

$\rightarrow 8 + 16 = c^2$

$\rightarrow 24 = c^2$

$\rightarrow \sqrt{24} = c$

$\rightarrow c= 2\sqrt{6}$

Compare your answer with the correct one above

Question

Find the length of the diagonal of the following cube:

Answer

To find the length of the diagonal, use the formula for a triangle:

$a-a-a\sqrt{2}$

$4\ m-4\ m-4\sqrt{2}\ m$

The length of the diagonal is $4\sqrt{2}\ m$ .

Compare your answer with the correct one above

Question

What is the diameter of a sphere with a volume of $36\pi$ ?

Answer

To find the diameter of a sphere we must use the equation for the volume of a sphere to find the radius which is half of the diameter.

The equation is

First we enter the volume into the equation yielding $36\pi=(\frac{4}{3})(\pi)(r^{3})$

We then divide each side by 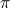to get $36=(\frac{4}{3})(r^{3})$

We then multiply each side by to get $27=r^{3}$

We then take the cubic root of each side to solve for the radius $\sqrt[3]{27}=\sqrt[3]{r^{3}}$

The radius is

We then multiply the radius by 2 to find the diameter

The answer for the diameter is .

Compare your answer with the correct one above

Question

If the surface area of a sphere is $64\pi$ , find the diameter of this sphere.

Answer

The standard equation to find the surface area of a sphere is

$SA=4\pi r^2$ where denotes the radius. Rearrange this equation in terms of :

$r=\sqrt{\frac{SA}{4\pi }}$

Substitute the given surface area into this equation and solve for the radius and then double the radius to get the diameter:

$r=\sqrt{\frac{64\Pi }{4\Pi }}=\sqrt{16}=4$

$diameter=2\cdot r=2\cdot 4=8$

Compare your answer with the correct one above

Question

Given that the volume of a sphere is $4\pi$ , find the diameter.

Answer

The standard equation to find the volume of a sphere is

$V=\frac{4}{3}\pi r^3$ where denotes the radius. Rearrange this equation in terms of :

$r=\sqrt[3]{\frac{3V}{4\pi }}$

Substitute the given volume into this equation and solve for the radius. Double the radius to find the diameter:

$r=\sqrt[3]{\frac{3V}{4\pi }}=\sqrt[3]{\frac{3\cdot 4\pi }{4\pi }}=\sqrt[3]{\frac{12\pi }{4\pi }}=\sqrt[3]{3 }$

$diameter=2\cdot r=2\sqrt[3]{3}$

Compare your answer with the correct one above

Question

The volume of a sphere is $2 8 8 \pi$ . What is the diameter?

Answer

To find the diameter of the sphere, we need to find the radius.

The volume of a sphere is $V=\frac{4}{3}\pi r^3$ .

Plug in our given values.

$2 88\pi=\frac{4}{3}\pi r^3$

Notice that the $\pi$ 's cancel out.

$288=\frac{4}{3}r^3$

$\frac{3}{4}*288=r^3$

$\sqrt[3]{216}=\sqrt[3]{r^3}$

The diameter is twice the radius, so .

Compare your answer with the correct one above

Question

What is the diameter of a sphere with a volume of $36\pi$ ?

Answer

The volume of a sphere is determined by the following equation:

$V=\frac{4}{3}\pi r^3$

$36\pi=\frac{4}{3}\pi r^3$

$(\frac{3}{4})36\pi=(\frac{3}{4})(\frac{4}{3})\pi r^3$

$\frac{27\pi}{\pi}=\frac{\pi r^3}{\pi}$

$\sqrt[3]{27}=\sqrt[3]{r^3}$

Compare your answer with the correct one above

Question

Our backyard pool holds 10,000 gallons. Its average depth is 4 feet deep and it is 10 feet long. If there are 7.48 gallons in a cubic foot, how wide is the pool?

Answer

There are 7.48 gallons in cubic foot. Set up a ratio:

1 ft3 / 7.48 gallons = x cubic feet / 10,000 gallons

Pool Volume = 10,000 gallons = 10,000 gallons * (1 ft3/ 7.48 gallons) = 1336.9 ft3

Pool Volume = 4ft x 10 ft x WIDTH = 1336.9 cubic feet

Solve for WIDTH:

4 ft x 10 ft x WIDTH = 1336.9 cubic feet

WIDTH = 1336.9 / (4 x 10) = 33.4 ft

Compare your answer with the correct one above

Question

A cube has a volume of 64cm3. What is the area of one side of the cube?

Answer

The cube has a volume of 64cm3, making the length of one edge 4cm (4 * 4 * 4 = 64).

So the area of one side is 4 * 4 = 16cm2

Compare your answer with the correct one above

Question

Given that the suface area of a cube is 72, find the length of one of its sides.

Answer

The standard equation for surface area is

where denotes side length. Rearrange the equation in terms of to find the length of a side with the given surface area:

$a=\sqrt{\frac{SA}{6}}=\sqrt{\frac{72}{6}}=\sqrt{12}=2\sqrt{3}$

Compare your answer with the correct one above

Question

Find the length of an edge of the following cube:

The volume of the cube is $27\ m^3$ .

Answer

The formula for the volume of a cube is

,

where is the length of the edge of a cube.

Plugging in our values, we get:

$27\ m^3 = (e)^3$

$e = 3\ m$

Compare your answer with the correct one above

Question

Find the length of an edge of the following cube:

The volume of the cube is $64\ m^3$ .

Answer

The formula for the volume of a cube is

,

where is the length of the edge of a cube.

Plugging in our values, we get:

$64\ m^3=(e)^3$

$e=4\ m$

Compare your answer with the correct one above

Question

What is the length of an edge of a cube that has a surface area of 54?

Answer

The surface area of a cube can be determined using the following equation:

$SA=6\times l^2$

$\frac{54}{6}=\frac{6l^2}{6}$

$\sqrt9=\sqrt{l^2}$

Compare your answer with the correct one above

Question

The length of a box is 3 times the width. Which of the following gives the length (L inches) in terms of the width (W inches) of the box?

Answer

When reading word problems, there are certain clues that help interpret what is going on. The word “is” generally means “=” and the word “times” means it will be multiplied by something. Therefore, “the length of a box is 3 times the width” gives you the answer: L = 3 x W, or L = 3W.

Compare your answer with the correct one above

Question

The width of a box, in inches, is 5 inches less than three times its length. Which of the following equations gives the width, W inches, in terms of the length, L inches, of the box?

Answer

We notice the width is “5 inches less than three times its width,” so we express W as being three times its width (3L) and 5 inches less than that is 3L minus 5. In this case, W is the dependent and L is the independent variable.

W = 3L - 5

Compare your answer with the correct one above

Question

Find the radius of a sphere whose surface area is $SA=100cm^{2}$ .

Answer

We know that the surface area of the spere is $SA=100cm^{2}$ .

$SA=4\pi r^{2}$

$100cm^{2}=4\pi r^{2}$

Rearrange and solve for .

$r^{2}=\frac{100cm^{2}}{4\pi}$

$\dpi{100} r=\sqrt{\frac{100cm^{2}}{4\pi}}$

$\dpi{100}\rightarrow 2.82cm$

Compare your answer with the correct one above

Question

What is the radius of a sphere that has a surface area of $16\pi$ ?

Answer

The standard equation to find the area of a sphere is $SA=4\pi r^2$ where denotes the radius. Rearrange this equation in terms of :

$r=\sqrt{\frac{SA}{4\pi }}$

To find the answer, substitute the given surface area into this equation and solve for the radius:

$r=\sqrt{\frac{16\pi }{4\pi }}=\sqrt{4}=2$

Compare your answer with the correct one above

Question

Given that the volume of a sphere is $12\pi$ , what is the radius?

Answer

The standard equation to find the volume of a sphere is

$V=\frac{4}{3}\pi r^3$ where denotes the radius. Rearrange this equation in terms of :

$r=\sqrt[3]{\frac{3V}{4\pi }}$

Substitute the given volume into this equation and solve for the radius:

$r=\sqrt[3]{\frac{3V}{4\pi }}=\sqrt[3]{\frac{3\cdot 12\pi }{4\pi }}=\sqrt[3]{\frac{36\pi }{4\pi }}=\sqrt[3]{9 }$

Compare your answer with the correct one above

Question

What is the radius of a sphere with a volume of $288\pi$ ?

Answer

$V=\frac{4}{3}\pi r^3$

$288\pi=\frac{4}{3}\pi r^3$

$\frac{288\pi}{\pi}=\frac{4\pi r^3}{3\pi}$

$288=\frac{4r^3}{3}$

$(288)(\frac{3}{4})=\frac{3}{4}(\frac{4r^3}{3})$

$\sqrt[3]{216}=\sqrt[3]{r^3}$

Compare your answer with the correct one above

Question

The lateral area is twice as big as the base area of a cone. If the height of the cone is 9, what is the entire surface area (base area plus lateral area)?

Answer

Lateral Area = LA = π(r)(l) where r = radius of the base and l = slant height

LA = 2B

π(r)(l) = 2π(r2)

rl = 2r2

l = 2r

From the diagram, we can see that r2 + h2 = l2. Since h = 9 and l = 2r, some substitution yields

r2 + 92 = (2r)2

r2 + 81 = 4r2

81 = 3r2

27 = r2

B = π(r2) = 27π

LA = 2B = 2(27π) = 54π

SA = B + LA = 81π

Compare your answer with the correct one above

Tap the card to reveal the answer