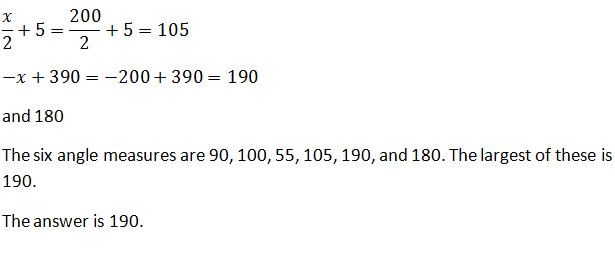Geometry - High School Math
Card 0 of 20
If a triangle has 180 degrees, what is the sum of the interior angles of a regular octagon?
If a triangle has 180 degrees, what is the sum of the interior angles of a regular octagon?
The sum of the interior angles of a polygon is given by  where
where  = number of sides of the polygon. An octagon has 8 sides, so the formula becomes
= number of sides of the polygon. An octagon has 8 sides, so the formula becomes 
The sum of the interior angles of a polygon is given by 

Compare your answer with the correct one above
What is the measure of an interior angle of a regular hexagon?
What is the measure of an interior angle of a regular hexagon?
The measure of an internal angle of an regular polygon can be determined using the following equation, where  equals the number of sides:
equals the number of sides:


The measure of an internal angle of an regular polygon can be determined using the following equation, where 
Compare your answer with the correct one above
In the parallellogram, what is the value of  ?
?

In the parallellogram, what is the value of 

Opposite angles are equal, and adjacent angles must sum to 180.
Therefore, we can set up an equation to solve for z:
(z – 15) + 2z = 180
3z - 15 = 180
3z = 195
z = 65
Now solve for x:
2_z_ = x = 130°
Opposite angles are equal, and adjacent angles must sum to 180.
Therefore, we can set up an equation to solve for z:
(z – 15) + 2z = 180
3z - 15 = 180
3z = 195
z = 65
Now solve for x:
2_z_ = x = 130°
Compare your answer with the correct one above
What is the interior angle measure of any regular pentagon?
What is the interior angle measure of any regular pentagon?
To find the angle of any regular polygon you find the number of sides  . For a pentagon,
. For a pentagon,  .
.
You then subtract 2 from the number of sides yielding 3.
Take 3 and multiply it by 180 degrees to yield the total number of degrees in the regular pentagon. 
Then to find one individual angle we divide 540 by the total number of angles 5, 
The answer is  .
.
To find the angle of any regular polygon you find the number of sides 

You then subtract 2 from the number of sides yielding 3.
Take 3 and multiply it by 180 degrees to yield the total number of degrees in the regular pentagon.
Then to find one individual angle we divide 540 by the total number of angles 5,
The answer is 
Compare your answer with the correct one above
What is the measure of each interior angle of a regular pentagon?
What is the measure of each interior angle of a regular pentagon?
The following equation can be used to determine the measure of an interior angle of a regular polygon, where  equals the number of sides.
equals the number of sides.

In a pentagon,  .
.

Now we can solve for the angle.

The following equation can be used to determine the measure of an interior angle of a regular polygon, where 
In a pentagon, 
Now we can solve for the angle.
Compare your answer with the correct one above
Find the interior angle of the following regular pentagon:

Find the interior angle of the following regular pentagon:

The formula for the sum of the interior angles of a polygon is
 ,
,
where  is the number of sides in the polygon
is the number of sides in the polygon
Plugging in our values, we get:


Dividing the sum of the interior angles by the number of angles in the polygon, we get the value for each interior angle:

The formula for the sum of the interior angles of a polygon is

where 
Plugging in our values, we get:
Dividing the sum of the interior angles by the number of angles in the polygon, we get the value for each interior angle:
Compare your answer with the correct one above
What is the measure of an interior angle of a regular pentagon?
What is the measure of an interior angle of a regular pentagon?
The measure of an interior angle of a regular polygon can be determined using the following equation, where  equals the number of sides:
equals the number of sides:


The measure of an interior angle of a regular polygon can be determined using the following equation, where 
Compare your answer with the correct one above
What is the magnitude of the interior angle of a regular nonagon?
What is the magnitude of the interior angle of a regular nonagon?
The equation to calculate the magnitude of an interior angle is  , where
, where  is equal to the number of sides.
is equal to the number of sides.
For our question,  .
.

The equation to calculate the magnitude of an interior angle is 

For our question, 
Compare your answer with the correct one above
What is the interior angle measure of any regular heptagon?
What is the interior angle measure of any regular heptagon?
To find the angle of any regular polygon you find the number of sides,  . In this example,
. In this example,  .
.
You then subtract 2 from the number of sides yielding 5.
Take 5 and multiply it by 180 degrees to yield the total number of degrees in the regular heptagon. 
Then to find one individual angle we divide 900 by the total number of angles, 7.

The answer is  .
.
To find the angle of any regular polygon you find the number of sides, 

You then subtract 2 from the number of sides yielding 5.
Take 5 and multiply it by 180 degrees to yield the total number of degrees in the regular heptagon.
Then to find one individual angle we divide 900 by the total number of angles, 7.
The answer is 
Compare your answer with the correct one above
A regular polygon with  sides has exterior angles that measure
sides has exterior angles that measure  each. How many sides does the polygon have?
each. How many sides does the polygon have?
A regular polygon with 

The sum of the exterior angles of any polygon, one per vertex, is  . As each angle measures
. As each angle measures  , just divide 360 by 1.5 to get the number of angles.
, just divide 360 by 1.5 to get the number of angles.

The sum of the exterior angles of any polygon, one per vertex, is 

Compare your answer with the correct one above
What is the interior angle measure of any regular nonagon?
What is the interior angle measure of any regular nonagon?
To find the angle of any regular polygon you find the number of sides  , which in this example is
, which in this example is  .
.
You then subtract  from the number of sides yielding
from the number of sides yielding  .
.
Take  and multiply it by
and multiply it by  degrees to yield a total number of degrees in the regular nonagon.
degrees to yield a total number of degrees in the regular nonagon.

Then to find one individual angle we divide  by the total number of angles
by the total number of angles  .
.

The answer is  .
.
To find the angle of any regular polygon you find the number of sides 

You then subtract 

Take 

Then to find one individual angle we divide 

The answer is 
Compare your answer with the correct one above
What is the measure of one exterior angle of a regular seventeen-sided polygon (nearest tenth of a degree)?
What is the measure of one exterior angle of a regular seventeen-sided polygon (nearest tenth of a degree)?
The sum of the measures of the exterior angles of any polygon, one per vertex, is  . In a regular polygon, all of these angles are congruent, so divide 360 by 17 to get the measure of one exterior angle:
. In a regular polygon, all of these angles are congruent, so divide 360 by 17 to get the measure of one exterior angle:

The sum of the measures of the exterior angles of any polygon, one per vertex, is 
Compare your answer with the correct one above
What is the measure of one exterior angle of a regular twenty-three-sided polygon (nearest tenth of a degree)?
What is the measure of one exterior angle of a regular twenty-three-sided polygon (nearest tenth of a degree)?
The sum of the measures of the exterior angles of any polygon, one per vertex, is  . In a regular polygon, all of these angles are congruent, so divide 360 by 23 to get the measure of one exterior angle:
. In a regular polygon, all of these angles are congruent, so divide 360 by 23 to get the measure of one exterior angle:

The sum of the measures of the exterior angles of any polygon, one per vertex, is 
Compare your answer with the correct one above
What is the measure of one interior angle of a regular twenty-three-sided polygon (nearest tenth of a degree)?
What is the measure of one interior angle of a regular twenty-three-sided polygon (nearest tenth of a degree)?
The measure of each interior angle of a regular polygon with  sides is
sides is  . We can substitute
. We can substitute  to obtain the angle measure:
to obtain the angle measure:

The measure of each interior angle of a regular polygon with 


Compare your answer with the correct one above
A regular polygon has interior angles which measure  each. How many sides does the polygon have?
each. How many sides does the polygon have?
A regular polygon has interior angles which measure 
The easiest way to answer this is to note that, since an interior angle and an exterior angle form a linear pair - and thus, a supplementary pair - each exterior angle would have measure  . Since 360 divided by the number of sides of a regular polygon is equal to the measure of one of its exterior angles, we are seeking
. Since 360 divided by the number of sides of a regular polygon is equal to the measure of one of its exterior angles, we are seeking  such that
such that

Solve for  :
:




The polygon has 20 sides.
The easiest way to answer this is to note that, since an interior angle and an exterior angle form a linear pair - and thus, a supplementary pair - each exterior angle would have measure 

Solve for 
The polygon has 20 sides.
Compare your answer with the correct one above
Acute angles x and y are inside a right triangle. If x is four less than one third of 21, what is y?
Acute angles x and y are inside a right triangle. If x is four less than one third of 21, what is y?
We know that the sum of all the angles must be 180 and we already know one angle is 90, leaving the sum of x and y to be 90.
Solve for x to find y.
One third of 21 is 7. Four less than 7 is 3. So if angle x is 3 then that leaves 87 for angle y.
We know that the sum of all the angles must be 180 and we already know one angle is 90, leaving the sum of x and y to be 90.
Solve for x to find y.
One third of 21 is 7. Four less than 7 is 3. So if angle x is 3 then that leaves 87 for angle y.
Compare your answer with the correct one above
If a right triangle has one leg with a length of 4 and a hypotenuse with a length of 8, what is the measure of the angle between the hypotenuse and its other leg?
If a right triangle has one leg with a length of 4 and a hypotenuse with a length of 8, what is the measure of the angle between the hypotenuse and its other leg?
The first thing to notice is that this is a 30o:60o:90o triangle. If you draw a diagram, it is easier to see that the angle that is asked for corresponds to the side with a length of 4. This will be the smallest angle. The correct answer is 30.
The first thing to notice is that this is a 30o:60o:90o triangle. If you draw a diagram, it is easier to see that the angle that is asked for corresponds to the side with a length of 4. This will be the smallest angle. The correct answer is 30.
Compare your answer with the correct one above

In the figure above, what is the positive difference, in degrees, between the measures of angle ACB and angle CBD?
In the figure above, what is the positive difference, in degrees, between the measures of angle ACB and angle CBD?
In the figure above, angle ADB is a right angle. Because side AC is a straight line, angle CDB must also be a right angle.
Let’s examine triangle ADB. The sum of the measures of the three angles must be 180 degrees, and we know that angle ADB must be 90 degrees, since it is a right angle. We can now set up the following equation.
x + y + 90 = 180
Subtract 90 from both sides.
x + y = 90
Next, we will look at triangle CDB. We know that angle CDB is also 90 degrees, so we will write the following equation:
y – 10 + 2_x_ – 20 + 90 = 180
y + 2_x_ + 60 = 180
Subtract 60 from both sides.
y + 2_x_ = 120
We have a system of equations consisting of x + y = 90 and y + 2_x_ = 120. We can solve this system by solving one equation in terms of x and then substituting this value into the second equation. Let’s solve for y in the equation x + y = 90.
x + y = 90
Subtract x from both sides.
y = 90 – x
Next, we can substitute 90 – x into the equation y + 2_x_ = 120.
(90 – x) + 2_x_ = 120
90 + x = 120
x = 120 – 90 = 30
x = 30
Since y = 90 – x, y = 90 – 30 = 60.
The question ultimately asks us to find the positive difference between the measures of ACB and CBD. The measure of ACB = 2_x_ – 20 = 2(30) – 20 = 40 degrees. The measure of CBD = y – 10 = 60 – 10 = 50 degrees. The positive difference between 50 degrees and 40 degrees is 10.
The answer is 10.
In the figure above, angle ADB is a right angle. Because side AC is a straight line, angle CDB must also be a right angle.
Let’s examine triangle ADB. The sum of the measures of the three angles must be 180 degrees, and we know that angle ADB must be 90 degrees, since it is a right angle. We can now set up the following equation.
x + y + 90 = 180
Subtract 90 from both sides.
x + y = 90
Next, we will look at triangle CDB. We know that angle CDB is also 90 degrees, so we will write the following equation:
y – 10 + 2_x_ – 20 + 90 = 180
y + 2_x_ + 60 = 180
Subtract 60 from both sides.
y + 2_x_ = 120
We have a system of equations consisting of x + y = 90 and y + 2_x_ = 120. We can solve this system by solving one equation in terms of x and then substituting this value into the second equation. Let’s solve for y in the equation x + y = 90.
x + y = 90
Subtract x from both sides.
y = 90 – x
Next, we can substitute 90 – x into the equation y + 2_x_ = 120.
(90 – x) + 2_x_ = 120
90 + x = 120
x = 120 – 90 = 30
x = 30
Since y = 90 – x, y = 90 – 30 = 60.
The question ultimately asks us to find the positive difference between the measures of ACB and CBD. The measure of ACB = 2_x_ – 20 = 2(30) – 20 = 40 degrees. The measure of CBD = y – 10 = 60 – 10 = 50 degrees. The positive difference between 50 degrees and 40 degrees is 10.
The answer is 10.
Compare your answer with the correct one above
Which of the following sets of line-segment lengths can form a triangle?
Which of the following sets of line-segment lengths can form a triangle?
In any given triangle, the sum of any two sides is greater than the third. The incorrect answers have the sum of two sides equal to the third.
In any given triangle, the sum of any two sides is greater than the third. The incorrect answers have the sum of two sides equal to the third.
Compare your answer with the correct one above