How to solve one-step equations - High School Math
Card 0 of 20
Michael buys two packs of pencils for  each and three sketch pads for
each and three sketch pads for  each. He pays for his purchase with
each. He pays for his purchase with  . How much change should he get?
. How much change should he get?
Michael buys two packs of pencils for 


First, calculate how much he spends on pencils and pads.
Pencils: 
Pads: 
Therefore the total spent is  .
.
Then the change is  .
.
First, calculate how much he spends on pencils and pads.
Pencils:
Pads:
Therefore the total spent is 
Then the change is 
Compare your answer with the correct one above
Solve for  if
if 
Solve for if
To solve for  we must get all of the numbers on the other side of the equation as
we must get all of the numbers on the other side of the equation as  .
.
To do this in a problem where a number is being added to  , we must subtract the number from both sides of the equation.
, we must subtract the number from both sides of the equation.
In this case the number is  so we subtract
so we subtract  from each side of the equation to make it look like this
from each side of the equation to make it look like this 
The numbers on the left side cancel to leave  by itself.
by itself.
To do the necessary subtraction we need to know how to subtract decimals from each other.
To subtract decimals you place the first decimal over the top of the other aligned by the decimal point.
Then go through each place and subtract the top number by the bottom number.
Subtract the numbers in each place like you would any number  and
and 
Combine the numbers and keep the decimal in the same place to get 
The answer is 
To solve for we must get all of the numbers on the other side of the equation as
.
To do this in a problem where a number is being added to , we must subtract the number from both sides of the equation.
In this case the number is 

The numbers on the left side cancel to leave by itself.
To do the necessary subtraction we need to know how to subtract decimals from each other.
To subtract decimals you place the first decimal over the top of the other aligned by the decimal point.
Then go through each place and subtract the top number by the bottom number.
Subtract the numbers in each place like you would any number 
Combine the numbers and keep the decimal in the same place to get
The answer is
Compare your answer with the correct one above
Solve for  if
if 
Solve for 
To solve for  we must get all of the numbers on the other side of the equation of
we must get all of the numbers on the other side of the equation of  .
.
To do this in a problem where  is being multiplied by a number, we must divide both sides of the equation by the number.
is being multiplied by a number, we must divide both sides of the equation by the number.
In this case the number is  so we divide each side of the equation by
so we divide each side of the equation by  to make it look like this
to make it look like this 
Then we must divide the decimals by each other to find the answer.
To divide decimals we line the decimals up like this  .
.
Then ignoring all of the decimal places we divide the top number by the bottom number to get 
Then we must apply the decimals.
However many decimal places there are in the denominator will be subtracted from the number of decimal places in the numerator to get the final number of decimal places in our answer.
If the number is positive we move the decimal that number of places to the left of our number.
If the number is negative we move the decimal that number of places to the right of our number.
In this case it would be  so we don't have any decimal places and the answer is
so we don't have any decimal places and the answer is  .
.
To solve for 

To do this in a problem where 
In this case the number is 

Then we must divide the decimals by each other to find the answer.
To divide decimals we line the decimals up like this 
Then ignoring all of the decimal places we divide the top number by the bottom number to get
Then we must apply the decimals.
However many decimal places there are in the denominator will be subtracted from the number of decimal places in the numerator to get the final number of decimal places in our answer.
If the number is positive we move the decimal that number of places to the left of our number.
If the number is negative we move the decimal that number of places to the right of our number.
In this case it would be 

Compare your answer with the correct one above
Solve for  if
if  .
.
Solve for if

We need to isolate x so that it is the only term on the left side of the equation.
To do this, add .16 to both sides of the equation:

The numbers on the left side cancel to leave  by itself.
by itself.

The answer is therefore  .
.
We need to isolate x so that it is the only term on the left side of the equation.
To do this, add .16 to both sides of the equation:
The numbers on the left side cancel to leave by itself.
The answer is therefore 
Compare your answer with the correct one above
Solve for  if
if  .
.
Solve for if

To solve for  we must get all of the numbers on the other side of the equation of
we must get all of the numbers on the other side of the equation of  .
.
To do this in a problem where  is being subtracted by a number, we must add the number to both sides of the equation.
is being subtracted by a number, we must add the number to both sides of the equation.
In this case the number is  so we add
so we add  to each side of the equation to make it look like this
to each side of the equation to make it look like this 
The numbers on the left side cancel to leave  by itself.
by itself.
Then we must perform the necessary addition to get the answer.
To add decimals together you place the decimals one over the top of the other aligned by the decimal point.
If there are no numbers after a tens, hundredths, or thousandths place or further to the right of the decimal just add a zero in the required areas.
Then add each place with the appropriately aligned number to get a result for each number.
In this case the decimals will add together like this 
The answer is  .
.
To solve for we must get all of the numbers on the other side of the equation of
.
To do this in a problem where is being subtracted by a number, we must add the number to both sides of the equation.
In this case the number is 

The numbers on the left side cancel to leave by itself.
Then we must perform the necessary addition to get the answer.
To add decimals together you place the decimals one over the top of the other aligned by the decimal point.
If there are no numbers after a tens, hundredths, or thousandths place or further to the right of the decimal just add a zero in the required areas.
Then add each place with the appropriately aligned number to get a result for each number.
In this case the decimals will add together like this
The answer is 
Compare your answer with the correct one above
Solve for  if
if 
Solve for 
To solve for  we must get all of the numbers on the other side of the equation of
we must get all of the numbers on the other side of the equation of  .
.
To do this in a problem where  is being multiplied by a coefficient, we must divide both sides of the equation by the coefficient.
is being multiplied by a coefficient, we must divide both sides of the equation by the coefficient.
In this case the number is  so we divide each side of the equation by
so we divide each side of the equation by  to make it look like this
to make it look like this 
Then we must divide the decimals by each other to find the answer.
To divide decimals we line the decimals up like this 
Then ignoring all of the decimal places we divide the top number by the bottom number to get 
Then we must apply the decimals.
The number of decimal places in the denominator will be subtracted from the number of decimal places in the numerator to get the number of decimal places we must change our answer.
If the number is positive we move the decimal that number of places to the left of our number.
If the number is negative we move the decimal that number of places to the right of our number.
In this case it would be negative so we move the decimal  place to the right of
place to the right of  to get
to get  .
.
The answer is  .
.
To solve for 

To do this in a problem where 
In this case the number is 

Then we must divide the decimals by each other to find the answer.
To divide decimals we line the decimals up like this
Then ignoring all of the decimal places we divide the top number by the bottom number to get
Then we must apply the decimals.
The number of decimal places in the denominator will be subtracted from the number of decimal places in the numerator to get the number of decimal places we must change our answer.
If the number is positive we move the decimal that number of places to the left of our number.
If the number is negative we move the decimal that number of places to the right of our number.
In this case it would be negative so we move the decimal 


The answer is 
Compare your answer with the correct one above

What is  ?
?
What is 
To solve  , you can either plug it into your calculator or convert it to a fraction. Since
, you can either plug it into your calculator or convert it to a fraction. Since  , we can rewrite the equation as:
, we can rewrite the equation as:


To solve 

Compare your answer with the correct one above
Solve for  if
if  .
.
Solve for if

To solve for  , we must isolate
, we must isolate  .
.
To do this in a problem where a number is being added to  , we must subtract the number from both sides of the equation.
, we must subtract the number from both sides of the equation.
In this case the number is  , so we subtract
, so we subtract  from each side of the equation to make it look like this:
from each side of the equation to make it look like this: 
The numbers on the left side cancel to leave 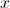 by itself.
by itself.
The answer is then  .
.
To solve for , we must isolate
.
To do this in a problem where a number is being added to , we must subtract the number from both sides of the equation.
In this case the number is 

The numbers on the left side cancel to leave by itself.
The answer is then 
Compare your answer with the correct one above
Solve for  if
if  .
.
Solve for if

To solve for  , we must move all of the constants to the other side of the equation as
, we must move all of the constants to the other side of the equation as  .
.
To do this in a problem where  is being multiplied by a number, we must divide both sides of the equation by the number.
is being multiplied by a number, we must divide both sides of the equation by the number.
In this case the number is  , so we divide each side of the equation by
, so we divide each side of the equation by  to make it look like this:
to make it look like this: 
Then we must divide the decimals by each other to find the answer.
To divide decimals we line the decimals up like this: 
Then, ignoring all of the decimal places, we divide the top number by the bottom number to get  .
.
Then we must move the decimals.
The number of decimal places in the denominator will be subtracted from the number of decimal places in the numerator to get the number of places to move the decimal point.
If the number is positive, we move the decimal that number of places to the left of our number.
If the number is negative, we move the decimal that number of places to the right of our number.
In this case the subtraction yields  , so we move the decimal
, so we move the decimal  place to the right of
place to the right of  to get
to get  .
.
The answer is  .
.
To solve for , we must move all of the constants to the other side of the equation as
.
To do this in a problem where is being multiplied by a number, we must divide both sides of the equation by the number.
In this case the number is 

Then we must divide the decimals by each other to find the answer.
To divide decimals we line the decimals up like this:
Then, ignoring all of the decimal places, we divide the top number by the bottom number to get 
Then we must move the decimals.
The number of decimal places in the denominator will be subtracted from the number of decimal places in the numerator to get the number of places to move the decimal point.
If the number is positive, we move the decimal that number of places to the left of our number.
If the number is negative, we move the decimal that number of places to the right of our number.
In this case the subtraction yields 



The answer is 
Compare your answer with the correct one above

Solve for  .
.
Solve for 
To solve  , add
, add  to both sides.
to both sides.



To solve 

Compare your answer with the correct one above

Solve for  .
.
Solve for 
To solve  , we need to isolate
, we need to isolate  . That means we need to add
. That means we need to add  to both sides.
to both sides.




To solve 


Compare your answer with the correct one above

Solve for  .
.
Solve for 
To solve  , you can either plug it into your calculator or realize that
, you can either plug it into your calculator or realize that  . Therefore, we are looking for half of five, which is
. Therefore, we are looking for half of five, which is  .
.
Mathematically, that means:


To solve 


Mathematically, that means:
Compare your answer with the correct one above

Solve for  .
.
Solve for 
To solve for  , we first need to isolate it. That means we want ONLY
, we first need to isolate it. That means we want ONLY  on the left side of the equation.
on the left side of the equation.

Subtract  from both sides.
from both sides.


To solve for 

Subtract 
Compare your answer with the correct one above
Solve for  when
when 
Solve for when
To solve for  we must get all of the numbers on the other side of the equation as
we must get all of the numbers on the other side of the equation as  .
.
To do this in a problem where a number is being added to  , we must subtract the number from both sides of the equation.
, we must subtract the number from both sides of the equation.
In this case the number is  so we subtract
so we subtract  from each side of the equation to make it look like this
from each side of the equation to make it look like this

The numbers on the left side cancel to leave 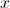 by itself.
by itself.
To do the necessary subtraction we need to know how to subtract decimals from each other.
To subtract decimals you place the first decimal over the top of the other aligned by the decimal point.
Then go through each place and subtract the top number by the bottom number.
Subtract the numbers in each place like you would any number.
Then combine them keeping the decimal in the same place to get  .
.
The answer is  .
.
To solve for we must get all of the numbers on the other side of the equation as
.
To do this in a problem where a number is being added to , we must subtract the number from both sides of the equation.
In this case the number is 

The numbers on the left side cancel to leave by itself.
To do the necessary subtraction we need to know how to subtract decimals from each other.
To subtract decimals you place the first decimal over the top of the other aligned by the decimal point.
Then go through each place and subtract the top number by the bottom number.
Subtract the numbers in each place like you would any number.
Then combine them keeping the decimal in the same place to get 
The answer is 
Compare your answer with the correct one above
Solve for 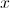 when
when

Solve for when
To solve for  we must get all of the numbers on the other side of the equation as
we must get all of the numbers on the other side of the equation as  .
.
To do this in a problem where  is being subtracted by a number, we must add the number to both sides of the equation.
is being subtracted by a number, we must add the number to both sides of the equation.
In this case the number is  so we add
so we add  to each side of the equation to make it look like this
to each side of the equation to make it look like this 
The numbers on the left side cancel to leave  by itself.
by itself.
Then we must perform the necessary addition to get the answer.
To add decimals together you place the decimals one over the top of the other aligned by the decimal point.
Then add each place with the appropriately aligned number to get a result for each number.
In this case the decimals will add together like this 
The answer is  .
.
To solve for we must get all of the numbers on the other side of the equation as
.
To do this in a problem where is being subtracted by a number, we must add the number to both sides of the equation.
In this case the number is 

The numbers on the left side cancel to leave by itself.
Then we must perform the necessary addition to get the answer.
To add decimals together you place the decimals one over the top of the other aligned by the decimal point.
Then add each place with the appropriately aligned number to get a result for each number.
In this case the decimals will add together like this
The answer is 
Compare your answer with the correct one above

Solve for  .
.
Solve for 
To solve for  , we need to isolate
, we need to isolate  . That means we want only
. That means we want only  on the left side of the equation.
on the left side of the equation.

Divide both sides by  .
.


To solve for 


Divide both sides by 
Compare your answer with the correct one above

Solve for  .
.
Solve for 
To solve  , we need to isolate
, we need to isolate  . That means we want just
. That means we want just  on the left hand side.
on the left hand side.
To do that, we need to divide both sides by  .
.




To solve 


To do that, we need to divide both sides by 
Compare your answer with the correct one above
What number is  of
of  ?
?
What number is 

Verbal cues include "IS" means equals and "OF" means multiplication.

Verbal cues include "IS" means equals and "OF" means multiplication.
Compare your answer with the correct one above
Solve for  .
.

Solve for 
Perform the same operation on both sides of the equation.

It will be easier to write the right side of the equation as a fraction.


Now, we add two-fifths to both sides of the equation.


Perform the same operation on both sides of the equation.
It will be easier to write the right side of the equation as a fraction.
Now, we add two-fifths to both sides of the equation.
Compare your answer with the correct one above
 is
is  % of what number?
% of what number?


To find the number of which  is
is  %, use this equation with
%, use this equation with  % expressed as a fraction coefficient:
% expressed as a fraction coefficient:

To solve this equation, multiply both sides of the equation by the reciprocal of the fraction on the left side, then reduce the result to simplest terms.


To find the number of which 


To solve this equation, multiply both sides of the equation by the reciprocal of the fraction on the left side, then reduce the result to simplest terms.
Compare your answer with the correct one above