Intermediate Single-Variable Algebra - High School Math
Card 0 of 20

Find the vertex of the parabola by completing the square.
Find the vertex of the parabola by completing the square.
To find the vertex of a parabola, we must put the equation into the vertex form:
![\small f(x)=a[b(x-h)]^{2}+k](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/108179/gif.latex)
The vertex can then be found with the coordinates (h, k).
To put the parabola's equation into vertex form, you have to complete the square. Completing the square just means adding the same number to both sides of the equation -- which, remember, doesn't change the value of the equation -- in order to create a perfect square.
Start with the original equation:

Put all of the  terms on one side:
terms on one side:

Now we know that we have to add something to both sides in order to create a perfect square:

In this case, we need to add 4 on both sides so that the right-hand side of the equation factors neatly.

Now we factor:
%5E%7B2%7D)
Once we isolate  , we have the equation in vertex form:
, we have the equation in vertex form:

Thus, the parabola's vertex can be found at  .
.
To find the vertex of a parabola, we must put the equation into the vertex form:
The vertex can then be found with the coordinates (h, k).
To put the parabola's equation into vertex form, you have to complete the square. Completing the square just means adding the same number to both sides of the equation -- which, remember, doesn't change the value of the equation -- in order to create a perfect square.
Start with the original equation:
Put all of the 
Now we know that we have to add something to both sides in order to create a perfect square:
In this case, we need to add 4 on both sides so that the right-hand side of the equation factors neatly.
Now we factor:
Once we isolate 
Thus, the parabola's vertex can be found at 
Compare your answer with the correct one above
Complete the square:

Complete the square:
Begin by dividing the equation by  and subtracting
and subtracting  from each side:
from each side:

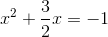
Square the value in front of the  and add to each side:
and add to each side:

Factor the left side of the equation:

Take the square root of both sides and simplify:
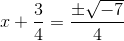
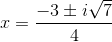
Begin by dividing the equation by 

Square the value in front of the 
Factor the left side of the equation:
Take the square root of both sides and simplify:
Compare your answer with the correct one above
Use factoring to solve the quadratic equation:

Use factoring to solve the quadratic equation:
Factor and solve:

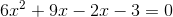
Factor like terms:

Combine like terms:
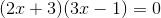

Factor and solve:
Factor like terms:
Combine like terms:
Compare your answer with the correct one above
Complete the square:

Complete the square:
Begin by dividing the equation by  and adding
and adding  to each side:
to each side:

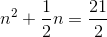
Square the value in front of the  and add to each side:
and add to each side:

Factor the left side of the equation:

Take the square root of both sides and simplify:



Begin by dividing the equation by 

Square the value in front of the 
Factor the left side of the equation:
Take the square root of both sides and simplify:
Compare your answer with the correct one above
Complete the square:
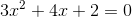
Complete the square:
Begin by dividing the equation by  and subtracting
and subtracting  from each side:
from each side:
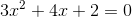

Square the value in front of the  and add to each side:
and add to each side:

Factor the left side of the equation:

Take the square root of both sides and simplify:


Begin by dividing the equation by 

Square the value in front of the 
Factor the left side of the equation:
Take the square root of both sides and simplify:
Compare your answer with the correct one above
Find the zeros.

Find the zeros.
This is a difference of perfect cubes so it factors to  . Only the first expression will yield an answer when set equal to 0, which is 1. The second expression will never cross the
. Only the first expression will yield an answer when set equal to 0, which is 1. The second expression will never cross the  -axis. Therefore, your answer is only 1.
-axis. Therefore, your answer is only 1.
This is a difference of perfect cubes so it factors to 

Compare your answer with the correct one above
Find the zeros.

Find the zeros.
Factor the equation to  . Set
. Set  and get one of your
and get one of your  's to be
's to be  . Then factor the second expression to
. Then factor the second expression to  . Set them equal to zero and you get
. Set them equal to zero and you get  .
.
Factor the equation to 





Compare your answer with the correct one above
Factor 
Factor
Use the difference of perfect cubes equation:

In  ,
,
 and
and ![b=\sqrt[3]{64}=4](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/94643/gif.latex)


Use the difference of perfect cubes equation:
In 

Compare your answer with the correct one above
Factor the polynomial completely and solve for  .
.

Factor the polynomial completely and solve for 
To factor and solve for  in the equation
in the equation 
Factor  out of the equation
out of the equation

Use the "difference of squares" technique to factor the parenthetical term, which provides the completely factored equation:

Any value that causes any one of the three terms  ,
,  , and
, and  to be
to be  will be a solution to the equation, therefore
will be a solution to the equation, therefore

To factor and solve for 
Factor 
Use the "difference of squares" technique to factor the parenthetical term, which provides the completely factored equation:
Any value that causes any one of the three terms 



Compare your answer with the correct one above
Factor the following expression:

Factor the following expression:
You can see that each term in the equation has an "x", therefore by factoring "x" from each term you can get that the equation equals  .
.
You can see that each term in the equation has an "x", therefore by factoring "x" from each term you can get that the equation equals 
Compare your answer with the correct one above
Factor this expression:

Factor this expression:
First consider all the factors of 12:
1 and 12
2 and 6
3 and 4
Then consider which of these pairs adds up to 7. This pair is 3 and 4.
Therefore the answer is  .
.
First consider all the factors of 12:
1 and 12
2 and 6
3 and 4
Then consider which of these pairs adds up to 7. This pair is 3 and 4.
Therefore the answer is 
Compare your answer with the correct one above
Factor the following polynomial:

Factor the following polynomial:
Begin by extracting  from the polynomial:
from the polynomial:


Now, factor the remainder of the polynomial as a difference of cubes:

Begin by extracting 
Now, factor the remainder of the polynomial as a difference of cubes:
Compare your answer with the correct one above
Factor the following polynomial:

Factor the following polynomial:
Begin by rearranging like terms:


Now, factor out like terms:

Rearrange the polynomial:

Begin by rearranging like terms:
Now, factor out like terms:
Rearrange the polynomial:
Compare your answer with the correct one above
Factor the following polynomial:

Factor the following polynomial:
Begin by rearranging like terms:


Now, factor out like terms:

Rearrange the polynomial:

Factor:


Begin by rearranging like terms:
Now, factor out like terms:
Rearrange the polynomial:
Factor:
Compare your answer with the correct one above
Factor the following polynomial:

Factor the following polynomial:
Begin by separating  into like terms. You do this by multiplying
into like terms. You do this by multiplying  and
and  , then finding factors which sum to
, then finding factors which sum to 


Now, extract like terms:

Simplify:

Begin by separating 


Now, extract like terms:
Simplify:
Compare your answer with the correct one above
Factor the following polynomial:

Factor the following polynomial:
To begin, distribute the squares:

![[(3a-4b)+(a+3b)][(3a-4b)-(a+3b)]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/153192/gif.latex)
Now, combine like terms:

To begin, distribute the squares:
Now, combine like terms:
Compare your answer with the correct one above
Factor the following polynomial:

Factor the following polynomial:
Begin by extracting  from the polynomial:
from the polynomial:


Now, distribute the cubic polynomial:

Begin by extracting 
Now, distribute the cubic polynomial:
Compare your answer with the correct one above
Factor the following polynomial:

Factor the following polynomial:
Begin by extracting like terms:


Now, rearrange the right side of the polynomial by reversing the signs:

Combine like terms:

Factor the square and cubic polynomial:

Begin by extracting like terms:
Now, rearrange the right side of the polynomial by reversing the signs:
Combine like terms:
Factor the square and cubic polynomial:
Compare your answer with the correct one above
Factor the following polynomial:

Factor the following polynomial:
Begin by rearranging the terms to group together the quadratic:


Now, convert the quadratic into a square:

Finally, distribute the  :
:

Begin by rearranging the terms to group together the quadratic:
Now, convert the quadratic into a square:
Finally, distribute the 
Compare your answer with the correct one above
Factor the following polynomial:

Factor the following polynomial:
Begin by extracting  from the polynomial:
from the polynomial:


Now, rearrange to combine like terms:

Extract the like terms and factor the cubic:
![mn[(m-n)(m^2+mn+n^2)+1(m-n)]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/153204/gif.latex)
Simplify by combining like terms:

Begin by extracting 
Now, rearrange to combine like terms:
Extract the like terms and factor the cubic:
Simplify by combining like terms:
Compare your answer with the correct one above