Functions and Graphs - High School Math
Card 0 of 20
Find the center and radius of the circle defined by the equation:

Find the center and radius of the circle defined by the equation:
The equation of a circle is:  where
where  is the radius and
is the radius and  is the center.
is the center.
In this problem, the equation is already in the format required to determine center and radius. To find the  -coordinate of the center, we must find the value of
-coordinate of the center, we must find the value of  that makes
that makes  equal to 0, which is 3. We do the same to find the y-coordinate of the center and find that
equal to 0, which is 3. We do the same to find the y-coordinate of the center and find that  . To find the radius we take the square root of the constant on the right side of the equation which is 6.
. To find the radius we take the square root of the constant on the right side of the equation which is 6.
The equation of a circle is: 


In this problem, the equation is already in the format required to determine center and radius. To find the 



Compare your answer with the correct one above
Find the center and radius of the circle defined by the equation:

Find the center and radius of the circle defined by the equation:
The equation of a circle is:  where
where  is the radius and
is the radius and  is the center.
is the center.
In this problem, the equation is already in the format required to determine center and radius. To find the  -coordinate of the center, we must find the value of
-coordinate of the center, we must find the value of  that makes
that makes  equal to
equal to  , which is
, which is  . We do the same to find the y-coordinate of the center and find that
. We do the same to find the y-coordinate of the center and find that  . To find the radius we take the square root of the constant on the right side of the equation which is 10.
. To find the radius we take the square root of the constant on the right side of the equation which is 10.
The equation of a circle is: 


In this problem, the equation is already in the format required to determine center and radius. To find the 





Compare your answer with the correct one above
Find the  -intercepts for the circle given by the equation:
-intercepts for the circle given by the equation:

Find the 
To find the  -intercepts (where the graph crosses the
-intercepts (where the graph crosses the  -axis), we must set
-axis), we must set  . This gives us the equation:
. This gives us the equation:

Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:
 and
and 
We can then solve these two equations to obtain  .
.
To find the 


Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:

We can then solve these two equations to obtain 
Compare your answer with the correct one above
Find the  -intercepts for the circle given by the equation:
-intercepts for the circle given by the equation:

Find the 
To find the  -intercepts (where the graph crosses the
-intercepts (where the graph crosses the  -axis), we must set
-axis), we must set  . This gives us the equation:
. This gives us the equation:


Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:
 and
and 
We can then solve these two equations to obtain
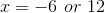
To find the 


Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:

We can then solve these two equations to obtain
Compare your answer with the correct one above
Solve:


Solve:
Use substution to solve this problem:
 becomes
becomes  and then is substituted into the second equation. Then solve for
and then is substituted into the second equation. Then solve for  :
:
 , so
, so  and
and  to give the solution
to give the solution  .
.
Use substution to solve this problem:







Compare your answer with the correct one above
Solve for the  - and
- and  - intercepts:
- intercepts:

Solve for the 

To solve for the  -intercept, set
-intercept, set  to zero and solve for
to zero and solve for  :
:




To solve for the  -intercept, set
-intercept, set  to zero and solve for
to zero and solve for  :
:




To solve for the 


To solve for the 


Compare your answer with the correct one above
Write 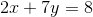 in slope-intercept form.
in slope-intercept form.
Write 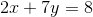
Slope-intercept form is  .
.



Slope-intercept form is 
Compare your answer with the correct one above
List the transformations that have been enacted upon the following equation:
![f(x)=4[6(x-3)]^{4}-7](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/106187/gif.latex)
List the transformations that have been enacted upon the following equation:
Since the equation given in the question is based off of the parent function  , we can write the general form for transformations like this:
, we can write the general form for transformations like this:
![g(x) = a[b(x-c)^{4}]+d](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/106188/gif.latex)
 determines the vertical stretch or compression factor.
determines the vertical stretch or compression factor.
- If
 is greater than 1, the function has been vertically stretched (expanded) by a factor of
is greater than 1, the function has been vertically stretched (expanded) by a factor of  .
.
- If
 is between 0 and 1, the function has been vertically compressed by a factor of
is between 0 and 1, the function has been vertically compressed by a factor of  .
.
In this case,  is 4, so the function has been vertically stretched by a factor of 4.
is 4, so the function has been vertically stretched by a factor of 4.
 determines the horizontal stretch or compression factor.
determines the horizontal stretch or compression factor.
- If
 is greater than 1, the function has been horizontally compressed by a factor of
is greater than 1, the function has been horizontally compressed by a factor of  .
.
- If
 is between 0 and 1, the function has been horizontally stretched (expanded) by a factor of
is between 0 and 1, the function has been horizontally stretched (expanded) by a factor of  .
.
In this case,  is 6, so the function has been horizontally compressed by a factor of 6. (Remember that horizontal stretch and compression are opposite of vertical stretch and compression!)
is 6, so the function has been horizontally compressed by a factor of 6. (Remember that horizontal stretch and compression are opposite of vertical stretch and compression!)
 determines the horizontal translation.
determines the horizontal translation.
- If
 is positive, the function was translated
is positive, the function was translated  units right.
units right.
- If
 is negative, the function was translated
is negative, the function was translated  units left.
units left.
In this case,  is 3, so the function was translated 3 units right.
is 3, so the function was translated 3 units right.
 determines the vertical translation.
determines the vertical translation.
- If
 is positive, the function was translated
is positive, the function was translated  units up.
units up.
- If
 is negative, the function was translated
is negative, the function was translated  units down.
units down.
In this case,  is -7, so the function was translated 7 units down.
is -7, so the function was translated 7 units down.
Since the equation given in the question is based off of the parent function 

- If
is greater than 1, the function has been vertically stretched (expanded) by a factor of
.
- If
is between 0 and 1, the function has been vertically compressed by a factor of
.
In this case, 

- If
is greater than 1, the function has been horizontally compressed by a factor of
.
- If
is between 0 and 1, the function has been horizontally stretched (expanded) by a factor of
.
In this case, 

- If
is positive, the function was translated
units right.
- If
is negative, the function was translated
units left.
In this case, 

- If
is positive, the function was translated
units up.
- If
is negative, the function was translated
units down.
In this case, 
Compare your answer with the correct one above
Find the radius of the circle given by the equation:

Find the radius of the circle given by the equation:
To find the center or the radius of a circle, first put the equation in the standard form for a circle:  , where
, where  is the radius and
is the radius and  is the center.
is the center.
From our equation, we see that it has not yet been factored, so we must do that now. We can use the formula  .
.
 , so
, so  .
.
 and
and  , so
, so  and
and  .
.
Therefore,  .
.
Because the constant, in this case 4, was not in the original equation, we need to add it to both sides:



Now we do the same for  :
:


We can now find  :
:

To find the center or the radius of a circle, first put the equation in the standard form for a circle: 


From our equation, we see that it has not yet been factored, so we must do that now. We can use the formula 






Therefore, 
Because the constant, in this case 4, was not in the original equation, we need to add it to both sides:
Now we do the same for 
We can now find 
Compare your answer with the correct one above
Find the center of the circle given by the equation:

Find the center of the circle given by the equation:
To find the center or the radius of a circle, first put the equation in standard form:  , where
, where  is the radius and
is the radius and  is the center.
is the center.
From our equation, we see that it has not yet been factored, so we must do that now. We can use the formula  .
.
 , so
, so  .
.
 and
and  , so
, so  and
and  .
.
This gives  .
.
Because the constant, in this case 9, was not in the original equation, we must add it to both sides:



Now we do the same for  :
:


We can now find the center: (3, -9)
To find the center or the radius of a circle, first put the equation in standard form: 


From our equation, we see that it has not yet been factored, so we must do that now. We can use the formula 






This gives 
Because the constant, in this case 9, was not in the original equation, we must add it to both sides:
Now we do the same for 
We can now find the center: (3, -9)
Compare your answer with the correct one above
The domain includes the values that go into a function (the x-values) and the range are the values that come out (the  or y-values). A sine curve represent a wave the repeats at a regular frequency. Based upon this graph, the maximum
or y-values). A sine curve represent a wave the repeats at a regular frequency. Based upon this graph, the maximum  is equal to 1, while the minimum is equal to –1. The x-values span all real numbers, as there is no limit to the input fo a sine function. The domain of the function is all real numbers and the range is
is equal to 1, while the minimum is equal to –1. The x-values span all real numbers, as there is no limit to the input fo a sine function. The domain of the function is all real numbers and the range is  .
.
The domain includes the values that go into a function (the x-values) and the range are the values that come out (the 


Compare your answer with the correct one above
If  , which of these values of
, which of these values of  is NOT in the domain of this equation?
is NOT in the domain of this equation?

If 

Using  as the input (
as the input ( ) value for this equation generates an output (
) value for this equation generates an output ( ) value that contradicts the stated condition of
) value that contradicts the stated condition of  .
.
Therefore  is not a valid value for
is not a valid value for  and not in the equation's domain:
and not in the equation's domain:

Using 



Therefore 

Compare your answer with the correct one above
What is the domain of the function?

What is the domain of the function?
The domain of a function is the set of possible values for the  variable. The range would be the possible values for the solution,
variable. The range would be the possible values for the solution,  .
.
The value inside of a square root must be greater than or equal to zero in order to have a real solution.

Now we can solve for  in the inequality.
in the inequality.



Square roots have positive and negative roots, so we need to set up two results. Remember to switch the direction fo the inequality for the negative solution.

These solutions can be combined to give our final answer.

Any values of  that are not included will result in an imaginary (impossible) answer.
that are not included will result in an imaginary (impossible) answer.
The domain of a function is the set of possible values for the 

The value inside of a square root must be greater than or equal to zero in order to have a real solution.
Now we can solve for 
Square roots have positive and negative roots, so we need to set up two results. Remember to switch the direction fo the inequality for the negative solution.
These solutions can be combined to give our final answer.
Any values of 
Compare your answer with the correct one above
Which of the following does NOT belong to the domain of the function  ?
?
Which of the following does NOT belong to the domain of the function 
The domain of a function includes all of the values of x for which f(x) is real and defined. In other words, if we put a value of x into the function, and we get a result that isn't real or is undefined, then that value won't be in the domain.
If we let x = 0, then we will be forced to evaluate  , which is equal to 1/0. The value of 1/0 is not defined, because we can never have zero in a denominator. Thus , because f(0) isn't defined, 0 cannot be in the domain of f(x).
, which is equal to 1/0. The value of 1/0 is not defined, because we can never have zero in a denominator. Thus , because f(0) isn't defined, 0 cannot be in the domain of f(x).
The answer is 0.
The domain of a function includes all of the values of x for which f(x) is real and defined. In other words, if we put a value of x into the function, and we get a result that isn't real or is undefined, then that value won't be in the domain.
If we let x = 0, then we will be forced to evaluate 
The answer is 0.
Compare your answer with the correct one above
What is the domain of the function:

What is the domain of the function:
The domain of a function consists of all of the possible values for x. In this case, we want to make sure that we are not dividing by  (
( in the denominator), since that would make our function undefined. Having
in the denominator), since that would make our function undefined. Having  would make the denominator
would make the denominator  . Thus, that is not in our domain. There is nothing else that would make this function undefined, and thus the domain is all real numbers except
. Thus, that is not in our domain. There is nothing else that would make this function undefined, and thus the domain is all real numbers except 
The domain of a function consists of all of the possible values for x. In this case, we want to make sure that we are not dividing by 



Compare your answer with the correct one above
Find the domain of the following function.

Find the domain of the following function.
Domain represents all possible values for  . In this situation, we want to make sure that the numbers under the square root are greater than or equal to 0. This will be the case when
. In this situation, we want to make sure that the numbers under the square root are greater than or equal to 0. This will be the case when  . Thus, the domain includes all real numbers such that
. Thus, the domain includes all real numbers such that  .
.
Domain represents all possible values for 


Compare your answer with the correct one above
What is the range of  ?
?
What is the range of 
The range of a function is defined as the possible values for  , or the possible outcomes. In this function, it is not possible to get any sort of negative number as an outcome. It is possible to get zero when
, or the possible outcomes. In this function, it is not possible to get any sort of negative number as an outcome. It is possible to get zero when  . Thus, the range is all real numbers greater than or equal to 0.
. Thus, the range is all real numbers greater than or equal to 0.
The range of a function is defined as the possible values for 

Compare your answer with the correct one above
What is the range of  ?
?
What is the range of 
The range of a function is all of the possible  values that the equation can take. For this equation our
values that the equation can take. For this equation our  value cannot be negative, as a negative number squared still gives us a positive value.
value cannot be negative, as a negative number squared still gives us a positive value.
Since  , we know that the lowest possible value that
, we know that the lowest possible value that  can reach is
can reach is  . Therefore the range is
. Therefore the range is  .
.
The range of a function is all of the possible 

Since 



Compare your answer with the correct one above
Which analysis can be performed to determine if an equation is a function?
Which analysis can be performed to determine if an equation is a function?
The vertical line test can be used to determine if an equation is a function. In order to be a function, there must only be one  (or
(or  ) value for each value of
) value for each value of  . The vertical line test determines how many
. The vertical line test determines how many  (or
(or  ) values are present for each value of
) values are present for each value of  . If a single vertical line passes through the graph of an equation more than once, it is not a function. If it passes through exactly once or not at all, then the equation is a function.
. If a single vertical line passes through the graph of an equation more than once, it is not a function. If it passes through exactly once or not at all, then the equation is a function.
The horizontal line test can be used to determine if a function is one-to-one, that is, if only one  value exists for each
value exists for each  (or
(or  ) value. Calculating zeroes, domain, and range can be useful for graphing an equation, but they do not tell if it is a function.
) value. Calculating zeroes, domain, and range can be useful for graphing an equation, but they do not tell if it is a function.
Example of a function: 
Example of an equation that is not a function: 
The vertical line test can be used to determine if an equation is a function. In order to be a function, there must only be one 





The horizontal line test can be used to determine if a function is one-to-one, that is, if only one 


Example of a function:
Example of an equation that is not a function:
Compare your answer with the correct one above
Evaluate  if
if  and
and  .
.
Evaluate 



This expression is the same as saying "take the answer of  and plug it into
and plug it into  ."
."
First, we need to find  . We do this by plugging
. We do this by plugging  in for
in for  in
in  .
.


Now we take this answer and plug it into  .
.

We can find the value of  by replacing
by replacing  with
with  .
.


This is our final answer.
This expression is the same as saying "take the answer of 

First, we need to find 



Now we take this answer and plug it into 
We can find the value of 


This is our final answer.
Compare your answer with the correct one above
 is a sine curve. What are the domain and range of this function?
is a sine curve. What are the domain and range of this function?