Algebra II - High School Math
Card 0 of 20

Find the vertex of the parabola by completing the square.
Find the vertex of the parabola by completing the square.
To find the vertex of a parabola, we must put the equation into the vertex form:
![\small f(x)=a[b(x-h)]^{2}+k](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/108179/gif.latex)
The vertex can then be found with the coordinates (h, k).
To put the parabola's equation into vertex form, you have to complete the square. Completing the square just means adding the same number to both sides of the equation -- which, remember, doesn't change the value of the equation -- in order to create a perfect square.
Start with the original equation:

Put all of the  terms on one side:
terms on one side:

Now we know that we have to add something to both sides in order to create a perfect square:

In this case, we need to add 4 on both sides so that the right-hand side of the equation factors neatly.

Now we factor:
%5E%7B2%7D)
Once we isolate  , we have the equation in vertex form:
, we have the equation in vertex form:

Thus, the parabola's vertex can be found at  .
.
To find the vertex of a parabola, we must put the equation into the vertex form:
The vertex can then be found with the coordinates (h, k).
To put the parabola's equation into vertex form, you have to complete the square. Completing the square just means adding the same number to both sides of the equation -- which, remember, doesn't change the value of the equation -- in order to create a perfect square.
Start with the original equation:
Put all of the 
Now we know that we have to add something to both sides in order to create a perfect square:
In this case, we need to add 4 on both sides so that the right-hand side of the equation factors neatly.
Now we factor:
Once we isolate 
Thus, the parabola's vertex can be found at 
Compare your answer with the correct one above
Complete the square:

Complete the square:
Begin by dividing the equation by  and subtracting
and subtracting  from each side:
from each side:

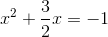
Square the value in front of the  and add to each side:
and add to each side:

Factor the left side of the equation:

Take the square root of both sides and simplify:
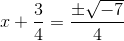
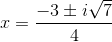
Begin by dividing the equation by 

Square the value in front of the 
Factor the left side of the equation:
Take the square root of both sides and simplify:
Compare your answer with the correct one above
Use factoring to solve the quadratic equation:

Use factoring to solve the quadratic equation:
Factor and solve:

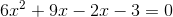
Factor like terms:

Combine like terms:
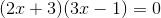

Factor and solve:
Factor like terms:
Combine like terms:
Compare your answer with the correct one above
Complete the square:

Complete the square:
Begin by dividing the equation by  and adding
and adding  to each side:
to each side:

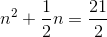
Square the value in front of the  and add to each side:
and add to each side:

Factor the left side of the equation:

Take the square root of both sides and simplify:



Begin by dividing the equation by 

Square the value in front of the 
Factor the left side of the equation:
Take the square root of both sides and simplify:
Compare your answer with the correct one above
Complete the square:
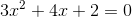
Complete the square:
Begin by dividing the equation by  and subtracting
and subtracting  from each side:
from each side:
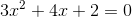

Square the value in front of the  and add to each side:
and add to each side:

Factor the left side of the equation:

Take the square root of both sides and simplify:


Begin by dividing the equation by 

Square the value in front of the 
Factor the left side of the equation:
Take the square root of both sides and simplify:
Compare your answer with the correct one above
Simplify the expression:

Simplify the expression:
Begin by distributing the exponent through the parentheses. The power rule dictates that an exponent raised to another exponent means that the two exponents are multiplied:

Any negative exponents can be converted to positive exponents in the denominator of a fraction:

The like terms can be simplified by subtracting the power of the denominator from the power of the numerator:


Begin by distributing the exponent through the parentheses. The power rule dictates that an exponent raised to another exponent means that the two exponents are multiplied:
Any negative exponents can be converted to positive exponents in the denominator of a fraction:
The like terms can be simplified by subtracting the power of the denominator from the power of the numerator:
Compare your answer with the correct one above
Order the following from least to greatest:





Order the following from least to greatest:
In order to solve this problem, each of the answer choices needs to be simplified.
Instead of simplifying completely, make all terms into a form such that they have 100 as the exponent. Then they can be easily compared.
 ,
,  ,
,  , and
, and  .
.
Thus, ordering from least to greatest:  .
.
In order to solve this problem, each of the answer choices needs to be simplified.
Instead of simplifying completely, make all terms into a form such that they have 100 as the exponent. Then they can be easily compared.




Thus, ordering from least to greatest: 
Compare your answer with the correct one above
What is the largest positive integer,  , such that
, such that  is a factor of
is a factor of  ?
?
What is the largest positive integer, 


 . Thus,
. Thus,  is equal to 16.
is equal to 16.


Compare your answer with the correct one above

Solve for  .
.
Solve for 
First, set up the equation: 
 . Simplifying this result gives
. Simplifying this result gives 
 .
.
First, set up the equation: 

Compare your answer with the correct one above
Convert the radical to exponential notation.
![\small \sqrt[4]{13}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/116532/gif.latex)
Convert the radical to exponential notation.
Remember that any term outside the radical will be in the denominator of the exponent.
![\sqrt[b]{x^a}=x^{\frac{a}{b}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/88790/gif.latex)
Since  does not have any roots, we are simply raising it to the one-fourth power.
does not have any roots, we are simply raising it to the one-fourth power.
![\sqrt[4]{13}=13^{\frac{1}{4}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/88791/gif.latex)
Remember that any term outside the radical will be in the denominator of the exponent.
Since 
Compare your answer with the correct one above
What is the value of  ?
?
What is the value of 
An exponent written as a fraction can be rewritten using roots.  can be reqritten as
can be reqritten as ![\sqrt[2]{9^5}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/92839/gif.latex) . The bottom number on the fraction becomes the root, and the top becomes the exponent you raise the number to.
. The bottom number on the fraction becomes the root, and the top becomes the exponent you raise the number to. ![\sqrt[2]{9^5}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/121574/gif.latex) is the same as
is the same as ![(\sqrt[2]{9})^{5}=3^{5}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/92840/gif.latex) . This will give us the answer of 243.
. This will give us the answer of 243.
An exponent written as a fraction can be rewritten using roots. 
![\sqrt[2]{9^5}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/92839/gif.latex)
![\sqrt[2]{9^5}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/121574/gif.latex)
![(\sqrt[2]{9})^{5}=3^{5}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/92840/gif.latex)
Compare your answer with the correct one above
Express the following radical in rational (exponential) form:

Express the following radical in rational (exponential) form:
To convert the radical to exponent form, begin by converting the integer:


Now, divide each exponent by  to clear the square root:
to clear the square root:

Finally, simplify the exponents:

To convert the radical to exponent form, begin by converting the integer:
Now, divide each exponent by 
Finally, simplify the exponents:
Compare your answer with the correct one above
Express the following radical in rational (exponential) form:
![\sqrt[3]{16x^5y^6z^8}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/152387/gif.latex)
Express the following radical in rational (exponential) form:
To convert the radical to exponent form, begin by converting the integer:
![\sqrt[3]{16x^5y^6z^8}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/152388/gif.latex)
![=\sqrt[3]{2^4x^5y^6z^8}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/152731/gif.latex)
Now, divide each exponent by  to remove the radical:
to remove the radical:

Finally, simplify the exponents:

To convert the radical to exponent form, begin by converting the integer:
Now, divide each exponent by 
Finally, simplify the exponents:
Compare your answer with the correct one above
Express the following radical in rational (exponential) form:
![\sqrt[4]{96a^5b^7c^8}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/152426/gif.latex)
Express the following radical in rational (exponential) form:
To convert the radical to exponent form, begin by converting the integer:
![\sqrt[4]{96a^5b^7c^8}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/152427/gif.latex)
![=\sqrt[4]{3\cdot 2^5a^5b^7c^8}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/152734/gif.latex)
Now, divide each exponent by  to cancel the radical:
to cancel the radical:

Finally, simplify the exponents:

To convert the radical to exponent form, begin by converting the integer:
Now, divide each exponent by 
Finally, simplify the exponents:
Compare your answer with the correct one above
Which fraction is equivalent to  ?
?
Which fraction is equivalent to 
Multiply the numerator and denominator by the compliment of the denominator:

Simplify the expression:

Multiply the numerator and denominator by the compliment of the denominator:
Simplify the expression:
Compare your answer with the correct one above
Simplify the following radical. Express in rational (exponential) form.

Simplify the following radical. Express in rational (exponential) form.
Multiply the numerator and denominator by the compliment of the denominator:

Simplify the expression:

Multiply the numerator and denominator by the compliment of the denominator:
Simplify the expression:
Compare your answer with the correct one above
Choose the fraction equivalent to  .
.
Choose the fraction equivalent to 
Multiply the numerator and denominator by the compliment of the denominator:


Simplify the expression:

Multiply the numerator and denominator by the compliment of the denominator:

Simplify the expression:
Compare your answer with the correct one above
Simplify the following radical. Express in rational (exponential) form.

Simplify the following radical. Express in rational (exponential) form.
Multiply the numerator and denominator to the exponent:


Simplify the expression by combining like terms:

Multiply the numerator and denominator to the exponent:
Simplify the expression by combining like terms:
Compare your answer with the correct one above
Simplify: 
Simplify:
Multiply the numerator and denominator to the exponent:


Simplify the expression by combining like terms:

Multiply the numerator and denominator to the exponent:
Simplify the expression by combining like terms:
Compare your answer with the correct one above
Express the following exponent in radical form:

Express the following exponent in radical form:
Begin by converting each exponent to have a denominator of  :
:


Now, rearrange into radical form:
![=\sqrt[6]{x^2y^3z^9}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/154779/gif.latex)
Finally, simplify:
![=z\sqrt[6]{x^2y^3z^3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/154780/gif.latex)
Begin by converting each exponent to have a denominator of 
Now, rearrange into radical form:
Finally, simplify:
Compare your answer with the correct one above