Algebra I - High School Math
Card 0 of 20
Which of the following lines is parallel to the line 
?
Which of the following lines is parallel to the line
Parallel lines have the same slope. In slope-intercept form, 
, 
is the slope.
Here the slope is 
; thus, any line that is parallel to the line in question will also have a slope of 
.
Only one answer choice satisfies this requirement: 
Note: the answer choice 
is incorrect. If put into 
form, the equation becomes 
. Therefore the slope is actually 
, not 
.
Parallel lines have the same slope. In slope-intercept form,
Here the slope is
Only one answer choice satisfies this requirement:
Note: the answer choice
Compare your answer with the correct one above
Which of the following lines is parallel to 
?
Which of the following lines is parallel to
Two lines that are parallel have the same slope. The slope of 
is 
, so we want another line with a slope of 
. The only other line with a slope of 
is 
.
Two lines that are parallel have the same slope. The slope of
Compare your answer with the correct one above
Which of these lines is parallel to 
?
Which of these lines is parallel to
Lines are parallel if they have the same slope. In standard 
form, 
is the slope.
For our given equation, the slope is 
. Only 
has the same slope.
Lines are parallel if they have the same slope. In standard
For our given equation, the slope is
Compare your answer with the correct one above
Which of these lines is parallel to 
?
Which of these lines is parallel to
Lines are parallel if they have the same slope. In standard 
form, 
is the slope.
For our given equation, the slope is 
. Only 
has the same slope.
Lines are parallel if they have the same slope. In standard
For our given equation, the slope is
Compare your answer with the correct one above
Which of the following lines will be parallel to 
?
Which of the following lines will be parallel to
Two lines are parallel if they have the same slope. When a line is in standard 
form, the 
is the slope.
For the given line 
, the slope will be 
. Only one other line has a slope of 
: 
Two lines are parallel if they have the same slope. When a line is in standard
For the given line
Compare your answer with the correct one above
Are the following lines parallel?
Are the following lines parallel?
By definition, two lines are parallel if they have the same slope. Notice that since we are given the lines in the 
format, and our slope is given by 
, it is clear that the slopes are not the same in this case, and thus the lines are not parallel.
By definition, two lines are parallel if they have the same slope. Notice that since we are given the lines in the
Compare your answer with the correct one above
Which of the following are perpendicular to the line with the formula 
?
I.
II. 
III. 
Which of the following are perpendicular to the line with the formula
I.
II.
III.
The slope of a perpendicular line is equal to the negative reciprocal of the original line. This means that the slope of our perpendicular line must be 3. We can also note that 
is also equal to 3, so both of these slopes are correct. The y-intercept does not matter, as the slope is the only thing that determines the slant of the line. Therefore, numerals I and III are both correct.
The slope of a perpendicular line is equal to the negative reciprocal of the original line. This means that the slope of our perpendicular line must be 3. We can also note that
Compare your answer with the correct one above
Which of the following lines is perpendicular to 
?
Which of the following lines is perpendicular to
In order for two lines to be perpendicular to each other, their slopes must be opposites and reciprocals of each other, meaning the fraction must be flipped upside down and the signs must be changed. In this situation, the original equation had a slope of 
, so the perpendicular slope must be 
.
In order for two lines to be perpendicular to each other, their slopes must be opposites and reciprocals of each other, meaning the fraction must be flipped upside down and the signs must be changed. In this situation, the original equation had a slope of
Compare your answer with the correct one above
Which of the following lines will be perpendicular to 
?
Which of the following lines will be perpendicular to
Two lines are perpendicular if they have opposite reciprocal slopes. When a line is in standard 
form, the 
is the slope. A perpendicular line will have a slope of 
.
The slope of our given line is 
. Therefore we want a slope of 
. The only line with the correct slope is 
.
Two lines are perpendicular if they have opposite reciprocal slopes. When a line is in standard
The slope of our given line is
Compare your answer with the correct one above
The points A, B, and C reside on a line segment. B is the midpoint of AC. If line AB measures 6 units in length, what is the length of line AC?
The points A, B, and C reside on a line segment. B is the midpoint of AC. If line AB measures 6 units in length, what is the length of line AC?
If B is the midpoint of AC, then AC is twice as long as AB. We are told that AB=6.
The diagram shows six units between points A and B, with B as the midpoint of segment AC. Therefore segment BC is also six units long, so line AC is twelve units long.
If B is the midpoint of AC, then AC is twice as long as AB. We are told that AB=6.
The diagram shows six units between points A and B, with B as the midpoint of segment AC. Therefore segment BC is also six units long, so line AC is twelve units long.
Compare your answer with the correct one above
What is the length of a line with endpoints 
and 
?
What is the length of a line with endpoints
The formula for the length of a line is very similiar to the pythagorean theorem:
Plug in our given numbers to solve:
The formula for the length of a line is very similiar to the pythagorean theorem:
Plug in our given numbers to solve:
Compare your answer with the correct one above
The center of a circle is 
and its radius is 
. Which of the following could be the equation of the circle?
The center of a circle is
The general equation of a circle is 
, where the center of the circle is 
and the radius is 
.
Thus, we plug the values given into the above equation to get 
.
The general equation of a circle is
Thus, we plug the values given into the above equation to get
Compare your answer with the correct one above
Which one of these equations accurately describes a circle with a center of 
and a radius of 
?
Which one of these equations accurately describes a circle with a center of
The standard formula for a circle is 
, with 
the center of the circle and 
the radius.
Plug in our given information.
This describes what we are looking for. This equation is not one of the answer choices, however, so subtract 
from both sides.
The standard formula for a circle is
Plug in our given information.
This describes what we are looking for. This equation is not one of the answer choices, however, so subtract
Compare your answer with the correct one above
What line goes through points 
and 
?
What line goes through points
First, we find the slope between the two points:
and 
Plug the slope and one point into the slope-intercept form to calculate the intercept:
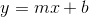
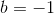
Thus the equation between the points becomes 
.
First, we find the slope between the two points:
Plug the slope and one point into the slope-intercept form to calculate the intercept:
Thus the equation between the points becomes
Compare your answer with the correct one above
What line is parallel to 
through the point 
?
What line is parallel to
The given line can be rewritten as 
, which has slope 
.
If the new line is parallel to the old line, it must have the same slope. So we use the point-slope form of an equation to calculate the new intercept.
becomes 
where 
.
So the equation of the parallel line is 
.
The given line can be rewritten as
If the new line is parallel to the old line, it must have the same slope. So we use the point-slope form of an equation to calculate the new intercept.
So the equation of the parallel line is
Compare your answer with the correct one above
Find the equation of a line parallel to the line that goes through points 
and 
.
Find the equation of a line parallel to the line that goes through points
Parallel lines share the same slope. Because the slope of the original line is 
, the correct answer must have that slope, so the correct answer is
Parallel lines share the same slope. Because the slope of the original line is
Compare your answer with the correct one above
Find the equation of a line parallel to 
.
Find the equation of a line parallel to
Since parallel lines share the same slope, the only answer that works is 
Since parallel lines share the same slope, the only answer that works is
Compare your answer with the correct one above
Given the equation 
and the point 
, find a line through the point that is parallel to the given line.
Given the equation
In order for two lines to be parallel, they must have the same slope. The slope of the given line is 
, so we know that the line going through the given point also has to have a slope of 
. Using the point-slope formula,
,
where 
represents the slope and 
and 
represent the given points, plug in the points given and simplify into standard form:
In order for two lines to be parallel, they must have the same slope. The slope of the given line is
where
Compare your answer with the correct one above
What line is parallel to 
through 
?
What line is parallel to
Parallel lines have the same slopes. The slope for the given equation is 
. We can use the slope and the new point in the slope intercept equation to solve for the intercept:
Therefore the new equation becomes:
Parallel lines have the same slopes. The slope for the given equation is
Therefore the new equation becomes:
Compare your answer with the correct one above
What line is parallel to 
through 
?
What line is parallel to
Parallel lines have the same slope. The slope of the given line is 
.
Find the line with slope 
through the point 
by plugging this informatuon into the slope intercept equation, 
:
, which gives 
.
Solve for 
by subtracting 
from both sides to get 
.
Then the parallel line equation becomes 
, and converting to standard form gives 
.
Parallel lines have the same slope. The slope of the given line is
Find the line with slope
Solve for
Then the parallel line equation becomes
Compare your answer with the correct one above