Sequences - GRE Subject Test: Math
Card 0 of 19
If a sequence is 9, 3, -3, -9, -15, ...
What is the 10th term of the sequence?
If a sequence is 9, 3, -3, -9, -15, ...
What is the 10th term of the sequence?
It will be helpful if you can see that the sequence is changing by -6 to get to each number. The quickest way to solve this is to keep going with the sequence by subtracting six from each number to get to the next number.
9, 3, -3, -9, -15, -21, -27, -33, -39, -45
-45 is the 10th number in the sequence.
Another way to find the 10th term is by using the equation for arithmetic sequences.

where  is the term in question,
is the term in question,  is the first term,
is the first term,  is the numbered term, and
is the numbered term, and  is the difference of the terms.
is the difference of the terms.
To find d subtract the first two terms.

Therefore, the equation becomes


It will be helpful if you can see that the sequence is changing by -6 to get to each number. The quickest way to solve this is to keep going with the sequence by subtracting six from each number to get to the next number.
9, 3, -3, -9, -15, -21, -27, -33, -39, -45
-45 is the 10th number in the sequence.
Another way to find the 10th term is by using the equation for arithmetic sequences.
where 



To find d subtract the first two terms.
Therefore, the equation becomes
Compare your answer with the correct one above
The first 3 terms of a geometric sequence are 5,9, and 13. What is the 15th term?
The first 3 terms of a geometric sequence are 5,9, and 13. What is the 15th term?
Step 1: We know it's a geometric sequence, so the difference between each consecutive term is the same. We must find the difference.

Step 2: For every term after the first term, we will add a multiple of  to the first term.
to the first term.
Step 3: We can write an equation that helps us find the nth term of the sequence. We add a multiple of 4n to 5; the equation becomes  .
.
Step 4: We need to find the value of n. We want the 15th number and we are given the first number. There are  numbers in between, so n=14.
numbers in between, so n=14.
Step 5: Plug in 14 for n and find the 15th term

The  term is
term is 
Step 1: We know it's a geometric sequence, so the difference between each consecutive term is the same. We must find the difference.
Step 2: For every term after the first term, we will add a multiple of 
Step 3: We can write an equation that helps us find the nth term of the sequence. We add a multiple of 4n to 5; the equation becomes 
Step 4: We need to find the value of n. We want the 15th number and we are given the first number. There are 
Step 5: Plug in 14 for n and find the 15th term
The 
Compare your answer with the correct one above
The first three terms of a arithmetic sequence are  . What is the
. What is the  term of this sequence?
term of this sequence?
The first three terms of a arithmetic sequence are 

Step 1: We need to find the difference between the terms. To find the difference, subtract the first two terms.
Difference=
Step 2: To find the next term of a arithmetic sequence, we add the difference to the previous term.
Fourth term= term+5
term+5
 term=
term= . The fourth term is 19.
. The fourth term is 19.
Step 3: To find the  term, we must add a multiple of
term, we must add a multiple of  to the first term. In this problem, we are given the
to the first term. In this problem, we are given the  term, so we need to find how many terms are in between the
term, so we need to find how many terms are in between the  and
and  term.
term.
 . This tells me that I have to add
. This tells me that I have to add  fourteen times to get to the
fourteen times to get to the  term.
term.  .
.
Step 4: Now that we know what the value of n, we can plug it in to the equation:
 , where 4 is the starting number, and n represents how many times I need to add 5 to the next term (and up to the 15th term).
, where 4 is the starting number, and n represents how many times I need to add 5 to the next term (and up to the 15th term).
Let's plug it in:
 .
.
So, the  term in this sequence is
term in this sequence is  .
.
Step 1: We need to find the difference between the terms. To find the difference, subtract the first two terms.
Difference=
Step 2: To find the next term of a arithmetic sequence, we add the difference to the previous term.
Fourth term=


Step 3: To find the 








Step 4: Now that we know what the value of n, we can plug it in to the equation:

Let's plug it in:

So, the 

Compare your answer with the correct one above
What is the next number in the sequence: 
What is the next number in the sequence:
Step 1: Try to find a pattern in the sequence




The pattern is decreasing perfect squares, the difference between each base of the consecutive term is  ..
..
Step 2: Find the next term...
If the base of the next term goes down by  , the next term is
, the next term is  ..
..

The next term of this sequence is  .
.
Step 1: Try to find a pattern in the sequence
The pattern is decreasing perfect squares, the difference between each base of the consecutive term is 
Step 2: Find the next term...
If the base of the next term goes down by 

The next term of this sequence is 
Compare your answer with the correct one above
What is the next term in the sequence: 
What is the next term in the sequence:
Step 1: Try to find the difference between the terms.
Difference between  and
and  is
is  .
.
Difference between  and
and  is
is  .
.
Difference between  and
and  is
is  .
.
Difference between  and
and  is
is  .
.
The difference between consecutive numbers is an odd number, and the difference between the consecutive terms is always  ..
..
The difference between  and
and  is
is 

The next number in the sequence is  .
.
Step 1: Try to find the difference between the terms.
Difference between 


Difference between 


Difference between 


Difference between 


The difference between consecutive numbers is an odd number, and the difference between the consecutive terms is always 
The difference between 

The next number in the sequence is 
Compare your answer with the correct one above
Find the next term in the sequence: 
Find the next term in the sequence:
Step 1: Find the next term in the sequence: 
Step 2: Can you recognize the sequence here??
This is the Fibonacci Sequence.. The sum of the previous two terms is equal to the next consecutive term..





The missing term is 13.
Step 1: Find the next term in the sequence:
Step 2: Can you recognize the sequence here??
This is the Fibonacci Sequence.. The sum of the previous two terms is equal to the next consecutive term..
The missing term is 13.
Compare your answer with the correct one above
What is the next term in the sequence: 
What is the next term in the sequence:
Step 1: Find the difference between each two consecutive terms...
The difference is always 6 because we have a sequence...
Step 2: Find the next term in the sequence..

The next term is  .
.
Step 1: Find the difference between each two consecutive terms...
The difference is always 6 because we have a sequence...
Step 2: Find the next term in the sequence..
The next term is 
Compare your answer with the correct one above
Find the next term in the following sequence: 
Find the next term in the following sequence:
Step 1: Calculate the difference between the terms...
 , add 9
, add 9
 , add 9
, add 9
 , add 9
, add 9
Step 2: We found the pattern between the terms..
So, we can add 9 to the term before the  to find the value of
to find the value of  ..
..

The missing term (the next term) in the sequence is  .
.
Step 1: Calculate the difference between the terms...



Step 2: We found the pattern between the terms..
So, we can add 9 to the term before the 

The missing term (the next term) in the sequence is 
Compare your answer with the correct one above
If the first term of an arithmetic sequence is 2 and the third term is 8, find the  th term.
th term.
If the first term of an arithmetic sequence is 2 and the third term is 8, find the 
Step 1: Find the difference between each term...
Subtract the first term from the third term...

There are two terms between first and third...Take the answer in step 1 and divide by 2 to get the difference between consecutive terms...

The common difference is  .
.
Step 2: Find an equation that describes the sequence....
The equation is  , where
, where  represents how many terms I need to calculate and
represents how many terms I need to calculate and  is the first term...
is the first term...
Step 3: Plug in  ...
...
To find n, we subtract the term that we want from the original term...
So, if we want the  th term and we are given the first term...
th term and we are given the first term...
Then 
So, 
The  th term is
th term is  .
.
Step 1: Find the difference between each term...
Subtract the first term from the third term...
There are two terms between first and third...Take the answer in step 1 and divide by 2 to get the difference between consecutive terms...
The common difference is 
Step 2: Find an equation that describes the sequence....
The equation is 


Step 3: Plug in 
To find n, we subtract the term that we want from the original term...
So, if we want the 
Then
So,
The 

Compare your answer with the correct one above
If the first  terms of a sequence are
terms of a sequence are  ,find the
,find the  th term.
th term.
If the first 


Step 1: Find the successive difference rows until we get equal values between every two consecutive numbers.



Step 2: Since we obtain equal values for the successive differences in the second row, hence the  term of the sequence is a second-degree polynomial.
term of the sequence is a second-degree polynomial.
So, the  term takes the form of
term takes the form of

Step 3: Now, substituting  into the formula, we get:
into the formula, we get:









Step 4: Solve the system of linear equations:

So, the  term takes the form:
term takes the form:

Step 5: Plug in  into the form...
into the form...



Step 1: Find the successive difference rows until we get equal values between every two consecutive numbers.
Step 2: Since we obtain equal values for the successive differences in the second row, hence the 
So, the 
Step 3: Now, substituting 
Step 4: Solve the system of linear equations:
So, the 
Step 5: Plug in 
Compare your answer with the correct one above
Which of the following are not infinite sequences?

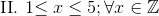
![$III. \sqrt[n]{x}; x \in \mathbb{R},n \in \mathbb{N}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/881613/gif.latex)
Which of the following are not infinite sequences?
Step 1: Define what an infinite sequence is...
An infinite sequence is a sequence that is non-terminating.
Step 2: Determine if each sequence above is infinite...
For  , the sequence is always infinite because the set of factorials is infinite. Also, the set of values by raising two factorial powers together is also infinite, it never has an ending term.
, the sequence is always infinite because the set of factorials is infinite. Also, the set of values by raising two factorial powers together is also infinite, it never has an ending term.
For 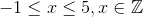 , this sequence is FINITE!
, this sequence is FINITE!
For ![\sqrt[n]{x}; x \in \mathbb{R},n \in \mathbb{N}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/881616/gif.latex) , this sequence is FINITE!
, this sequence is FINITE!
Step 1: Define what an infinite sequence is...
An infinite sequence is a sequence that is non-terminating.
Step 2: Determine if each sequence above is infinite...
For 
For 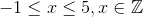
For ![\sqrt[n]{x}; x \in \mathbb{R},n \in \mathbb{N}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/881616/gif.latex)
Compare your answer with the correct one above
Find the radius of convergence for the power series

Find the radius of convergence for the power series
We can use the limit

to find the radius of convergence. We have
![\small \small \lim_{n\to\infty} \left| \frac{a_{n+1}}{a_n} \right|=\lim \left| \frac{x^{n+1}[(n+1)!]^2}{(2(n+1))!} \frac{(2n!)}{(n!)^2x^n}\right|](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/383920/gif.latex)
![\small \small \small \small =\lim |x|\left| \frac{(2n)!}{(2n+2)!} \frac{[(n+1)!]^2}{(n!)^2}\right|=\lim |x|\left| \frac{(n+1)(n+1)}{(2n+1)(2n+2)}\right|=\frac{|x|}{4}<1](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/383921/gif.latex)

This means the radius of convergence is  .
.
We can use the limit
to find the radius of convergence. We have
This means the radius of convergence is 
Compare your answer with the correct one above
Determine if the following series is divergent, convergent or neither.

Determine if the following series is divergent, convergent or neither.
In order to figure if

is convergent, divergent or neither, we need to use the ratio test.
Remember that the ratio test is as follows.
Suppose we have a series  . We define,
. We define,

Then if
 , the series is absolutely convergent.
, the series is absolutely convergent.
 , the series is divergent.
, the series is divergent.
 , the series may be divergent, conditionally convergent, or absolutely convergent.
, the series may be divergent, conditionally convergent, or absolutely convergent.
Now lets apply the ratio test to our problem.
Let

and

Now

 .
.
Now lets simplify this expression to


 .
.
Since  ,
,
we have sufficient evidence to conclude that the series is divergent.
In order to figure if
is convergent, divergent or neither, we need to use the ratio test.
Remember that the ratio test is as follows.
Suppose we have a series 
Then if



Now lets apply the ratio test to our problem.
Let
and
Now

Now lets simplify this expression to

Since 
we have sufficient evidence to conclude that the series is divergent.
Compare your answer with the correct one above
Calculate the sum of the following infinite geometric series:

Calculate the sum of the following infinite geometric series:
This is an infinite geometric series.
The sum of an infinite geometric series can be calculated with the following formula,
 , where
, where  is the first value of the summation, and r is the common ratio.
is the first value of the summation, and r is the common ratio.
Solution:
Value of  can be found by setting
can be found by setting 

r is the value contained in the exponent




This is an infinite geometric series.
The sum of an infinite geometric series can be calculated with the following formula,


Solution:
Value of 
r is the value contained in the exponent
Compare your answer with the correct one above
Determine how many terms need to be added to approximate the following series within  :
:

Determine how many terms need to be added to approximate the following series within 
This is an alternating series test.
In order to find the terms necessary to approximate the series within  first see if the series is convergent using the alternating series test. If the series converges, find n such that
first see if the series is convergent using the alternating series test. If the series converges, find n such that 
Step 1:
An alternating series can be identified because terms in the series will “alternate” between + and –, because of 
Note: Alternating Series Test can only show convergence. It cannot show divergence.
If the following 2 tests are true, the alternating series converges.


- {
 } is a decreasing sequence, or in other words
} is a decreasing sequence, or in other words 
Solution:

1. 

2. { } is a decreasing functon, since a factorial never decreases.
} is a decreasing functon, since a factorial never decreases.
Since the 2 tests pass, this series is convergent.
Step 2:
Plug in n values until 


4 needs to be added to approximate the sum within  .
.
This is an alternating series test.
In order to find the terms necessary to approximate the series within 
Step 1:
An alternating series can be identified because terms in the series will “alternate” between + and –, because of
Note: Alternating Series Test can only show convergence. It cannot show divergence.
If the following 2 tests are true, the alternating series converges.
- {
} is a decreasing sequence, or in other words
Solution:
1.
2. {
Since the 2 tests pass, this series is convergent.
Step 2:
Plug in n values until
4 needs to be added to approximate the sum within 
Compare your answer with the correct one above
You have a divergent series  , and you multiply it by a constant 10. Is the new series
, and you multiply it by a constant 10. Is the new series  convergent or divergent?
convergent or divergent?
You have a divergent series 

This is a fundamental property of series.
For any constant c, if  is convergent then
is convergent then  is convergent, and if
is convergent, and if  is divergent,
is divergent,  is divergent.
is divergent.
 is divergent in the question, and the constant c is 10 in this case, so
is divergent in the question, and the constant c is 10 in this case, so  is also divergent.
is also divergent.
This is a fundamental property of series.
For any constant c, if 





Compare your answer with the correct one above
There are 2 series,  and
and  , and they are both convergent. Is
, and they are both convergent. Is  convergent, divergent, or inconclusive?
convergent, divergent, or inconclusive?
There are 2 series, 


Infinite series can be added and subtracted with each other.

Since the 2 series are convergent, the sum of the convergent infinite series is also convergent.
Note: The starting value, in this case n=1, must be the same before adding infinite series together.
Infinite series can be added and subtracted with each other.
Since the 2 series are convergent, the sum of the convergent infinite series is also convergent.
Note: The starting value, in this case n=1, must be the same before adding infinite series together.
Compare your answer with the correct one above
There are 2 series  and
and  .
.
Is the sum of these 2 infinite series convergent, divergent, or inconclusive?
There are 2 series 

Is the sum of these 2 infinite series convergent, divergent, or inconclusive?
A way to find out if the sum of the 2 infinite series is convergent or not is to find out whether the individual infinite series are convergent or not.
Test the first series
 .
.
This is a geometric series with  .
.
By the geometric test, this series is convergent.
Test the second series
 .
.
This is a geometric series with  .
.
By the geometric test, this series is convergent.
Since both of the series are convergent,  is also convergent.
is also convergent.
A way to find out if the sum of the 2 infinite series is convergent or not is to find out whether the individual infinite series are convergent or not.
Test the first series

This is a geometric series with 
By the geometric test, this series is convergent.
Test the second series

This is a geometric series with 
By the geometric test, this series is convergent.
Since both of the series are convergent, 
Compare your answer with the correct one above
Evaluate:  . (Round to 4 places)
. (Round to 4 places)
Evaluate: 
Step 1: Plug in values into the function and add up the fraction:

Step 2: Find the sum of the fractions....
We can convert the fractions to decimals:


Step 3: Round to  places...
places...

Step 1: Plug in values into the function and add up the fraction:
Step 2: Find the sum of the fractions....
We can convert the fractions to decimals:
Step 3: Round to 
Compare your answer with the correct one above