Limits - GRE Subject Test: Math

Card 0 of 20

Question

Evaluate: $\lim_{x \to 2} \frac {x-2}{x^2-4}$

Answer

Step 1: See if we can plug in into the equation..

We can't because the denominator becomes ..

Step 2: Factor the denominator:

(By the Difference of Perfect Squares Formula)

Step 3: Re-write the function:

$\frac {(x-2)}{[(x-2)(x+2)]}$

Step 4: Divide by on both the numerator and denominator because it's common:

We are left with: $\frac {1}{(x+2)}$

Step 5: Plug in :

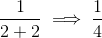
$\frac {1}{2+2}\implies \frac {1}{4}$

The limit of this function as x approaches 2 is $\frac {1}{4}$ .

Compare your answer with the correct one above

Question

Evaluate:

$\lim_{x\rightarrow 0^{+} } \frac{x \sin x}{2^{x} - 1}$

Answer

$\lim_{x\rightarrow 0^{+} } x \sin x= 0 \cdot \sin 0 = 0$

and

$\lim_{x\rightarrow 0^{+} } \left ( 2 ^{x} - 1 \right )= 2^{0} -1 = 0$

Therefore, by L'Hospital's Rule, we can find $\lim_{x\rightarrow 0^{+} } \frac{x \sin x}{2^{x} - 1}$ by taking the derivatives of the expressions in both the numerator and the denominator:

$\frac{\mathrm{d} }{\mathrm{d} x}x \sin x = \frac{\mathrm{d} }{\mathrm{d} x} x \cdot \sin x + \frac{\mathrm{d} }{\mathrm{d} x}\sin x \cdot x$

$= 1 \cdot \sin x + \cos x \cdot x = \sin x + x \cos x$

$\frac{\mathrm{d} }{\mathrm{d} x}\left ( 2^{x} - 1 \right ) = \frac{\mathrm{d} }{\mathrm{d} x}\left ( e^{x \ln 2} - 1 \right )$

$= \frac{\mathrm{d} }{\mathrm{d} x} e^{x \ln 2} - \frac{\mathrm{d} }{\mathrm{d} x} 1$

$= \ln 2\cdot e^{x \ln 2} - 0 = \ln 2\cdot 2^{x }$

$\lim_{x\rightarrow 0^{+} } \frac{x \sin x}{2^{x} - 1} = \lim_{x\rightarrow 0^{+} } \frac{\sin x + x \cos x}{ \ln 2\cdot 2^{x }}$

$= \frac{\sin 0 + 0 \cos 0}{ \ln 2\cdot 2^{0 }} = \frac{ 0 + 0 }{ \ln 2\cdot 1} = 0$

Compare your answer with the correct one above

Question

Evaluate:

$\lim_{x\rightarrow \infty } \frac{x \sin^{2} x}{2^{x} - 1}$

Answer

Let's examine the limit

$\lim_{x\rightarrow \infty } \frac{x }{2^{x} - 1}$

first.

$\lim_{x\rightarrow \infty }x= \lim_{x\rightarrow \infty } \left ( 2^{x} - 1 \right )= \infty$

$\frac{\mathrm{d} }{\mathrm{d} x}x = 1$

and

$\frac{\mathrm{d} }{\mathrm{d} x}\left ( 2^{x} - 1 \right ) = \frac{\mathrm{d} }{\mathrm{d} x}\left ( e^{ x \ln 2} - 1 \right )$

$= \frac{\mathrm{d} }{\mathrm{d} x}e^{ x \ln 2} - \frac{\mathrm{d} }{\mathrm{d} x} 1$

$=\ln 2 \cdot e^{ x \ln 2} - 0 = \ln 2 \cdot 2^{x}$ ,

so by L'Hospital's Rule,

$\lim_{x\rightarrow \infty } \frac{x }{2^{x} - 1} = \lim_{x\rightarrow \infty } \frac{1 }{\ln 2 \cdot 2^{x}}$

Since $\lim_{x\rightarrow \infty } \ln 2 \cdot 2^{x} = \infty$ ,

$\lim_{x\rightarrow \infty } \frac{x }{2^{x} - 1} = \lim_{x\rightarrow \infty } \frac{1 }{\ln 2 \cdot 2^{x}} = 0$

Now, for each , $0 \leq \sin^{2} x \leq 1$ ; therefore,

$0 \leq \frac{x \sin^{2} x}{2^{x} - 1} \leq \frac{x }{2^{x} - 1}$

By the Squeeze Theorem,

$0 \leq \lim_{x\rightarrow \infty } \frac{x \sin^{2} x}{2^{x} - 1} \leq \lim_{x\rightarrow \infty } \frac{x }{2^{x} - 1} = 0$

and

$\lim_{x\rightarrow \infty } \frac{x \sin^{2} x}{2^{x} - 1} = 0$

Compare your answer with the correct one above

Question

Evaluate:

$\lim_{x\rightarrow \infty } \frac{5^{x} - 1}{3^{x} - 1}$

Answer

$\lim_{x\rightarrow \infty }\left ( 5^{x} - 1 \right ) = \lim_{x\rightarrow \infty }\left ( 3^{x} - 1 \right ) = \infty$

Therefore, by L'Hospital's Rule, we can find $\lim_{x\rightarrow \infty } \frac{5^{x} - 1}{3^{x} - 1}$ by taking the derivatives of the expressions in both the numerator and the denominator:

$\frac{\mathrm{d} }{\mathrm{d} x}\left ( 5^{x} - 1 \right ) = \frac{\mathrm{d} }{\mathrm{d} x}\left ( e^{x \ln 5} - 1 \right )$

$= \frac{\mathrm{d} }{\mathrm{d} x} e^{x \ln 5 } - \frac{\mathrm{d} }{\mathrm{d} x}1$

$=\ln 5\cdot e^{x \ln 5 } - 0 = \ln 5\cdot 5^{x }$

Similarly,

$\frac{\mathrm{d} }{\mathrm{d} x}\left ( 3^{x} - 1 \right ) = \ln 3 \cdot 3 ^{x}$

So

$\lim_{x\rightarrow \infty } \frac{5^{x} - 1}{3^{x} - 1} = \lim_{x\rightarrow \infty } \frac{\ln 5 \cdot 5^{x} }{\ln 3 \cdot 3^{x} }$

$=\frac{\ln 5 }{\ln 3 } \cdot \lim_{x\rightarrow \infty } \frac{ 5^{x} }{ 3^{x} }= \frac{\ln 5 }{\ln 3 } \cdot \lim_{x\rightarrow \infty }\left ( \frac{ 5 }{ 3 } \right )^{x}$

But $\lim_{x\rightarrow \infty }a^{x} = \infty$ for any , so

$\lim_{x\rightarrow \infty } \frac{5^{x} - 1}{3^{x} - 1}= \frac{\ln 5 }{\ln 3 } \cdot \lim_{x\rightarrow \infty }\left ( \frac{ 5 }{ 3 } \right )^{x} = \infty$

Compare your answer with the correct one above

Question

Evaluate:

$\lim_{x\rightarrow 0 } \frac{7^{x} - 1}{2^{x} - 1}$

Answer

$\lim_{x\rightarrow 0 }\left ( 7^{x} - 1 \right ) = 7^{0} - 1 = 1- 1 = 0$

and

$\lim_{x\rightarrow 0 }\left ( 2^{x} - 1 \right ) = 2^{0} - 1 = 1- 1 = 0$

Therefore, by L'Hospital's Rule, we can find $\lim_{x\rightarrow 0 } \frac{7^{x} - 1}{2^{x} - 1}$ by taking the derivatives of the expressions in both the numerator and the denominator:

$\frac{\mathrm{d} }{\mathrm{d} x}\left ( 7^{x} - 1 \right ) = \frac{\mathrm{d} }{\mathrm{d} x}\left ( e^{x \ln 7} - 1 \right )$

$= \frac{\mathrm{d} }{\mathrm{d} x} e^{x \ln 7 } - \frac{\mathrm{d} }{\mathrm{d} x}1$

$=\ln 7\cdot e^{x \ln 7 } - 0 = \ln 7\cdot 7^{x }$

Similarly,

$\frac{\mathrm{d} }{\mathrm{d} x}\left ( 2^{x} - 1 \right ) = \ln 2 \cdot 2 ^{x}$

so

$\lim_{x\rightarrow 0 } \frac{7^{x} - 1}{2^{x} - 1} = \lim_{x\rightarrow 0 } \frac{ \ln 7\cdot 7^{x }}{ \ln 2\cdot 2^{x }}$

$= \frac{ \ln 7 \cdot 7^{0 }}{ \ln 2\cdot 2^{0 }} = \frac{ \ln 7\cdot 1}{ \ln 2\cdot 1} = \frac{ \ln 7}{ \ln 2 }= \log_{2}7$

Compare your answer with the correct one above

Question

Calculate the following limit.

$\lim_{x\rightarrow2} \frac{x^2-4}{2x-4}$

Answer

To calculate the limit, often times we can just plug in the limit value into the expression. However, in this case if we were to do that we get $\frac00$ , which is undefined.

What we can do to fix this is use L'Hopital's rule, which says

$\lim_{x\rightarrow 2} \frac{f(x)}{g(x)}=\lim_{x\rightarrow 2} \frac{f'(x)}{g'(x)}$ .

So, L'Hopital's rule allows us to take the derivative of both the top and the bottom and still obtain the same limit.

$\lim_{x-\rightarrow 2} \frac{x^2-4}{2x-4}=\lim_{x\rightarrow 2} \frac{2x}{2}$ .

Plug in to get an answer of .

Compare your answer with the correct one above

Question

Calculate the following limit.

$\lim_{x\rightarrow \infty} \frac{5x^2+2x+1}{x^4+2}$

Answer

If we plugged in the integration limit to the expression in the problem we would get $\frac{\infty}{\infty}$ , which is undefined. Here we use L'Hopital's rule, which is shown below.

$\lim_{x\rightarrow a} \frac{f(x)}{g(x)}=\lim_{x\rightarrow a} \frac{f'(x)}{g'(x)}$

This gives us,

$\lim_{x\rightarrow \infty} \frac{5x^2+2x+1}{x^4+2}=\lim_{x\rightarrow \infty} \frac{10x+2}{4x^3}$ .

However, even with this simplified limit, we still get $\frac{\infty}{\infty}$ . So what do we do? We do L'Hopital's again!

$\lim_{x\rightarrow \infty} \frac{10x+2}{4x^3}=\lim_{x\rightarrow \infty} \frac{10}{12x^2}$ .

Now if we plug in infitinity, we get 0.

$\frac{10}{\infty}=0$

Compare your answer with the correct one above

Question

Solve:

${}\lim_{x \to \infty} x^\frac{5}{x}}$

Answer

Substitution is invalid. In order to solve ${}{ \lim_{x \to \infty} x^\frac{5}{x}}$ , rewrite this as an equation.

${} y= { \lim_{x \to \infty} x^\frac{5}{x}}$

Take the natural log of both sides to bring down the exponent.

${} \lim_{x \to \infty} ln(y)= \lim_{x \to \infty} \frac{5}{x} \cdot ln(x)$

${} \lim_{x \to \infty} ln(y)= 5\lim_{x \to \infty} \frac{ln(x)}{x}$

Since ${} \lim_{x \to \infty} \frac{ln(x)}{x}$ is in indeterminate form, ${}\frac{\infty}{\infty}$ , use the L'Hopital Rule.

L'Hopital Rule is as follows:

$\lim_{x\rightarrow \infty} \frac{f(x)}{g(x)}=\lim_{x\rightarrow \infty}\frac{f'(x)}{g'(x)}$

${} \lim_{x \to \infty} \frac{ln(x)}{x} = \lim_{x \to \infty} \frac{\frac{1}{x}}{1} = 0$

This indicates that the right hand side of the equation is zero.

${} \lim_{x \to \infty} ln(y)= 0$

Use the term to eliminate the natural log.

${} \lim_{x \to \infty} e^l^n^(^y^)= e^0$

$\lim_{x \to \infty} y=e^0=1$

Compare your answer with the correct one above

Question

Find the

$\small \small \small \lim_{x\rightarrow 0}\frac{e^{x^{2}}-ln(1+x)-1}{cosx-sinx-1}$ .

Answer

Subbing in zero into $\small \frac{(e^{x^{2}}-ln(1+x)-1)}{cosx-sinx-1}$ will give you $\small \frac{0}{0}$ , so we can try to use L'hopital's Rule to solve.

First, let's find the derivative of the numerator.

$\small e^{x^{2}}$ is in the form $\small a^{u}$ , which has the derivative $\small a^{u}u'lna$ , so its derivative is $\small 2xe^{x^{2}}$ .

$\small ln(1+x)$ is in the form $\small lnu$ , which has the derivative $\small u'/u$ , so its derivative is $\small 1/(1+x)$ .

The derivative of $\small 1$ is $\small 0$ so the derivative of the numerator is $\small 2xe^{x^{2}}-1/(1+x)$ .

In the denominator, the derivative of $\small cosx$ is $\small -sinx$ , and the derivative of $\small sinx$ is $\small cosx$ . Thus, the entire denominator's derivative is $\small -(sinx+cosx)$ .

Now we take the

$\small \lim_{x\rightarrow 0}\frac{2xe^{x^{2}}-1/(x+1)}{-(sinx+cosx)}$ , which gives us $\small \frac{-1}{-1}=1$ .

Compare your answer with the correct one above

Question

Evaluate the limit using L'Hopital's Rule.

$\lim_{x\rightarrow \infty }\frac{x^2}{e^x+1}$

Answer

L'Hopital's Rule is used to evaluate complicated limits. The rule has you take the derivative of both the numerator and denominator individually to simplify the function. In the given function we take the derivatives the first time and get

$\lim_{x\rightarrow \infty }\frac{2x}{e^x}$ .

This still cannot be evaluated properly, so we will take the derivative of both the top and bottom individually again. This time we get

$\lim_{x\rightarrow \infty }\frac{2}{e^x}$ .

Now we have only one x, so we can evaluate when x is infinity. Plug in infinity for x and we get

$\frac{2}{e^\infty }$ and $e^\infty=\infty$ .

So we can simplify the function by remembering that any number divided by infinity gives you zero.

Compare your answer with the correct one above

Question

Evaluate the limit using L'Hopital's Rule.

$\lim_{x \to 0} \frac{2x^2}{ln(x)}$

Answer

L'Hopital's Rule is used to evaluate complicated limits. The rule has you take the derivative of both the numerator and denominator individually to simplify the function. In the given function we take the derivatives the first time and get

$\lim_{x\rightarrow 0}\frac{4x}{\frac{1}{x}}=\lim_{x\rightarrow 0}4x^2$ .

Since the first set of derivatives eliminates an x term, we can plug in zero for the x term that remains. We do this because the limit approaches zero.

This gives us

$4\cdot 0^2=0$ .

Compare your answer with the correct one above

Question

Evaluate the limit using L'Hopital's Rule.

$\lim_{x\rightarrow \infty }\frac{5x^3+1}{3x^2}$

Answer

L'Hopital's Rule is used to evaluate complicated limits. The rule has you take the derivative of both the numerator and denominator individually to simplify the function. In the given function we take the derivatives the first time and get

$\lim_{x\rightarrow \infty }\frac{15x^2}{6x}$ .

This still cannot be evaluated properly, so we will take the derivative of both the top and bottom individually again. This time we get

$\lim_{x\rightarrow \infty }\frac{30x}{6}=5x$ .

Now we have only one x, so we can evaluate when x is infinity. Plug in infinity for x and we get

$5\cdot \infty=\infty$ .

Compare your answer with the correct one above

Question

Calculate the following limit.

$\lim_{x->-\infty}\frac{e^{-2x}}{x^2}$

Answer

If we plugged in $-\infty$ directly, we would get an indeterminate value of $\frac{\infty}{\infty}$ .

We can use L'Hopital's rule to fix this. We take the derivate of the top and bottom and reevaluate the same limit.

$\lim_{x->-\infty}\frac{e^{-2x}}{x^2}=-\frac{e^{-2x}}{x}$ .

We still can't evaluate the limit of the new expression, so we do it one more time.

$\lim_{x->-\infty}-\frac{e^{-2x}}{x}=\lim_{x->-\infty}2e^{-2x}=\infty$

Compare your answer with the correct one above

Question

Evaluate the following limit.

$\lim_{x->0}\frac{sin(x)}{ln(x)}$

Answer

If we plug in 0 into the limit we get $\frac{0}{0}$ , which is indeterminate.

We can use L'Hopital's rule to fix this. We can take the derivative of the top and bottom and reevaluate the limit.

$\lim_{x->0}\frac{sin(x)}{ln(x)}=\lim_{x->0}xcos(x)=0$ .

Now if we plug in 0, we get 0, so that is our final limit.

Compare your answer with the correct one above

Question

Evaluate the following limit

$\small \lim_{x\to 0} \frac{\cos x-(x-1)^2}{x^3-3x}$

if possible.

Answer

If we try to directly plug in the limit value into the function, we get

$\small \small \frac{\cos 0-(0-1)^2}{0^3-3\cdot 0}=\frac{1-1}{0-0}=\frac{0}{0}$

Because the limit is of the form $\small \frac{0}{0}$ , we can apply L'Hopital's rule to "simplify" the limit to

$\small \small \lim_{x\to 0} \frac{\cos x-(x-1)^2}{x^3-3x}=\lim_{x\to 0} \frac{\sin x-2(x-1)}{3x^2-3}$ .

Now if we directly plug in 0 again, we get

$\small \small \small \lim_{x\to 0} \frac{\cos x-(x-1)^2}{x^3-3x}=\lim_{x\to 0} \frac{\sin x-2(x-1)}{3x^2-3}=\frac{0-2(0-1)}{0-3}=-\frac{2}{3}$ .

Compare your answer with the correct one above

Question

Evaluate the following limit:

$\lim_{t\rightarrow 2}\frac{t^2-4}{\sin (2-t)}$

Answer

When you try to solve the limit using normal methods, you find that the limit approaches zero in the numerator and denominator, resulting in an indeterminate form "0/0".

In order to evaluate the limit, we must use L'Hopital's Rule, which states that:

$\lim_{x\rightarrow a}\frac{f(x)}{g(x)}=\lim_{x\rightarrow a}\frac{f'(x)}{g'(x)}$

when an indeterminate form occurs when evaluting the limit.

Next, simply find f'(x) and g'(x) for this limit:

$2t, -\cos(2-t)$

The derivatives were found using the following rules:

$\frac{d}{dx}(x^n)=nx^{n-1}$ , $\frac{d}{dx}\sin(u)=\cos(u)\frac{du}{dx}$

Next, using L'Hopital's Rule, evaluate the limit using f'(x) and g'(x):

$\lim_{t\rightarrow 2}\frac{2t}{-\cos (2-t)}=-4$

Compare your answer with the correct one above

Question

Find the limit:

$\lim_{x \to 0} \frac{cos(x)-1}{tan(x)}$

Answer

In order to determine the limit, substitute to determine whether the expression is indeterminate.

$\lim_{x \to 0} \frac{cos(x)-1}{tan(x)} = \frac{0}{0}$

Use the L'Hopital's rule to simplify. Take the derivative of the numerator and denominator separately, and reapply the limit.

$\lim_{x \to 0} \frac{-sin(x)}{sec^2(x)}= -sin(x)\times \frac{1}{cos(x)}\times \frac{1}{cos(x)}$

Substitute

$-sin(0)\times \frac{1}{cos(0)}\times \frac{1}{cos(0)} =0$

Compare your answer with the correct one above

Question

Evaluate:

$\lim_{x\to 3}\frac{(x-3)^2}{(3-x)^2}$

Answer

By substitution, the limit will yield an indeterminate form $\frac{0}{0}$ . L'Hopital can be used in this scenario.

Take the derivative of the numerator and denominator separately, and then reapply the limit.

$\lim_{x\to 3}\frac{(x-3)^2}{(3-x)^2}=\lim_{x\to 3}\frac{2(x-3)}{-2(3-x)}=\lim_{x\to 3}-\frac{x-3}{3-x}=\lim_{x\to 3}-\frac{x-3}{-(x-3)}=1$

The answer is .

Compare your answer with the correct one above

Question

Determine the limit of:

$\lim_{n\to \infty} \left(\frac{n+1}{n}\right)^2$

Answer

Rewrite the expression.

$\lim_{n\to \infty} (\frac{n+1}{n})^2= \lim_{n\to \infty} \frac{(n+1)^2}{n^2}$

By substitutition, we will get the indeterminate form $\frac{\infty}{\infty}$ .

The L'Hopital's rule can be used to solve for the limit. Write the L'Hopital's rule.

$\lim_{x\to a} \frac{f(x)}{g(x)}= \lim_{x\to a} \frac{f'(x)}{g'(x)}$

Apply this rule twice.

$\lim_{n\to \infty} \frac{(n+1)^2}{n^2}=\lim_{n\to \infty} \frac{2(n+1)}{2n}=\lim_{n\to \infty} \frac{2}{2}=1$

Compare your answer with the correct one above

Question

Evaluate the following limit:

$\lim_{x\rightarrow 0}\frac{x}{\sin(x)}$

Answer

When evaluating the limit using normal methods (substitution), you find that the indeterminate form of $\frac{0}{0}$ is reached. To evaluate the limit, we can use L'Hopital's Rule, which states that:

$\lim_{x\rightarrow a}\frac{f(x)}{g(x)}=\lim_{x\rightarrow a}\frac{f'(x)}{g'(x)}$

So, we find the derivative of the numerator and denominator, which is

and $\cos(x)$ , respectively.

The derivatives were found using the following rules:

$\frac{d}{dx}(x^n)=nx^{n-1}$ , $\frac{d}{dx}\sin(x)=\cos(x)$

When we evaluate this new limit, we find that

$\lim_{x\rightarrow 0}\frac{1}{cos(x)}=1$ .

Compare your answer with the correct one above

Tap the card to reveal the answer