Right Triangles - GRE Quantitative Reasoning
Card 0 of 20
A triangle has three internal angles of 75, 60, and x. What is x?
A triangle has three internal angles of 75, 60, and x. What is x?
The internal angles of a triangle must add up to 180. 180 - 75 -60= 45.
The internal angles of a triangle must add up to 180. 180 - 75 -60= 45.
Compare your answer with the correct one above
Quantitative Comparison
Quantity A: The area of a triangle with a perimeter of 34
Quantity B: 30
Quantitative Comparison
Quantity A: The area of a triangle with a perimeter of 34
Quantity B: 30
A triangle with a fixed perimeter does not have to have a fixed area. For example, a triangle with sides 3, 4, and 5 has a perimeter of 12 and an area of 6. A triangle with sides 4, 4, and 4 also has a perimeter of 12 but not an area of 6. Thus the answer cannot be determined.
A triangle with a fixed perimeter does not have to have a fixed area. For example, a triangle with sides 3, 4, and 5 has a perimeter of 12 and an area of 6. A triangle with sides 4, 4, and 4 also has a perimeter of 12 but not an area of 6. Thus the answer cannot be determined.
Compare your answer with the correct one above
Quantitative Comparison
Column A
Area
Column B
Perimeter
Quantitative Comparison
Column A
Area
Column B
Perimeter
To find the perimeter, add up the sides, here 5 + 12 + 13 = 30. To find the area, multiply the two legs together and divide by 2, here (5 * 12)/2 = 30.
To find the perimeter, add up the sides, here 5 + 12 + 13 = 30. To find the area, multiply the two legs together and divide by 2, here (5 * 12)/2 = 30.
Compare your answer with the correct one above
Given triangle ACE where B is the midpoint of AC, what is the area of triangle ABD?
Given triangle ACE where B is the midpoint of AC, what is the area of triangle ABD?
If B is a midpoint of AC, then we know AB is 12. Moreover, triangles ACE and ABD share angle DAB and have right angles which makes them similar triangles. Thus, their sides will all be proportional, and BD is 4. 1/2bh gives us 1/2 * 12 * 4, or 24.
If B is a midpoint of AC, then we know AB is 12. Moreover, triangles ACE and ABD share angle DAB and have right angles which makes them similar triangles. Thus, their sides will all be proportional, and BD is 4. 1/2bh gives us 1/2 * 12 * 4, or 24.
Compare your answer with the correct one above
What is the area of a right triangle with hypotenuse of 13 and base of 12?
What is the area of a right triangle with hypotenuse of 13 and base of 12?
Area = 1/2(base)(height). You could use Pythagorean theorem to find the height or, if you know the special right triangles, recognize the 5-12-13. The area = 1/2(12)(5) = 30.
Area = 1/2(base)(height). You could use Pythagorean theorem to find the height or, if you know the special right triangles, recognize the 5-12-13. The area = 1/2(12)(5) = 30.
Compare your answer with the correct one above
Quantitative Comparison
Quantity A: the area of a right triangle with sides 10, 24, 26
Quantity B: twice the area of a right triangle with sides 5, 12, 13
Quantitative Comparison
Quantity A: the area of a right triangle with sides 10, 24, 26
Quantity B: twice the area of a right triangle with sides 5, 12, 13
Quantity A: area = base * height / 2 = 10 * 24 / 2 = 120
Quantity B: 2 * area = 2 * base * height / 2 = base * height = 5 * 12 = 60
Therefore Quantity A is greater.
Quantity A: area = base * height / 2 = 10 * 24 / 2 = 120
Quantity B: 2 * area = 2 * base * height / 2 = base * height = 5 * 12 = 60
Therefore Quantity A is greater.
Compare your answer with the correct one above
Quantitative Comparison
Quantity A: The area of a triangle with a height of 6 and a base of 7
Quantity B: Half the area of a trapezoid with a height of 6, a base of 6, and another base of 10
Quantitative Comparison
Quantity A: The area of a triangle with a height of 6 and a base of 7
Quantity B: Half the area of a trapezoid with a height of 6, a base of 6, and another base of 10
Quantity A: Area = 1/2 * b * h = 1/2 * 6 * 7 = 42/2 = 21
Quantity B: Area = 1/2 * (_b_1 + _b_2) * h = 1/2 * (6 + 10) * 6 = 48
Half of the area = 48/2 = 24
Quantity B is greater.
Quantity A: Area = 1/2 * b * h = 1/2 * 6 * 7 = 42/2 = 21
Quantity B: Area = 1/2 * (_b_1 + _b_2) * h = 1/2 * (6 + 10) * 6 = 48
Half of the area = 48/2 = 24
Quantity B is greater.
Compare your answer with the correct one above
The radius of the circle is 2. What is the area of the shaded equilateral triangle?
The radius of the circle is 2. What is the area of the shaded equilateral triangle?
This is easier to see when the triangle is divided into six parts (blue). Each one contains an angle which is half of 120 degrees and contains a 90 degree angle. This means each triangle is a 30/60/90 triangle with its long side equal to the radius of the circle. Knowing that means that the height of each triangle is 
and the base is 
.
Applying 
and multiplying by 6 gives 
).
This is easier to see when the triangle is divided into six parts (blue). Each one contains an angle which is half of 120 degrees and contains a 90 degree angle. This means each triangle is a 30/60/90 triangle with its long side equal to the radius of the circle. Knowing that means that the height of each triangle is
Applying
Compare your answer with the correct one above
An equilateral triangle has a side length of 4. What is its height?
An equilateral triangle has a side length of 4. What is its height?
If an equilateral triangle is divided in 2, it forms two 30-60-90 triangles. Therefore, the side of the equilateral triangle is the same as the hypotenuse of a 30-60-90 triangle. The side lengths of a 30-60-90 triangle adhere to the ratio x: x√3 :2x. since we know the hypothesis is 4, we also know that the base is 2 and the height is 2√3.
If an equilateral triangle is divided in 2, it forms two 30-60-90 triangles. Therefore, the side of the equilateral triangle is the same as the hypotenuse of a 30-60-90 triangle. The side lengths of a 30-60-90 triangle adhere to the ratio x: x√3 :2x. since we know the hypothesis is 4, we also know that the base is 2 and the height is 2√3.
Compare your answer with the correct one above
Each of the following answer choices lists the side lengths of a different triangle. Which of these triangles does not have a right angle?
Each of the following answer choices lists the side lengths of a different triangle. Which of these triangles does not have a right angle?
cannot be the side lengths of a right triangle. 
does not equal 
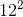. Also, special right triangle 
and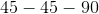 
rules can eliminate all the other choices.
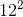
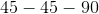
Compare your answer with the correct one above
Daria and Ashley start at the same spot and walk their two dogs to the park, taking different routes. Daria walks 1 mile north and then 1 mile east. Ashley walks her dog on a path going northeast that leads directly to the park. How much further does Daria walk than Ashley?
Daria and Ashley start at the same spot and walk their two dogs to the park, taking different routes. Daria walks 1 mile north and then 1 mile east. Ashley walks her dog on a path going northeast that leads directly to the park. How much further does Daria walk than Ashley?
First let's calculate how far Daria walks. This is simply 1 mile north + 1 mile east = 2 miles. Now let's calculate how far Ashley walks. We can think of this problem using a right triangle. The two legs of the triangle are the 1 mile north and 1 mile east, and Ashley's distance is the diagonal. Using the Pythagorean Theorem we calculate the diagonal as √(12 + 12) = √2. So Daria walked 2 miles, and Ashley walked √2 miles. Therefore the difference is simply 2 – √2 miles.
First let's calculate how far Daria walks. This is simply 1 mile north + 1 mile east = 2 miles. Now let's calculate how far Ashley walks. We can think of this problem using a right triangle. The two legs of the triangle are the 1 mile north and 1 mile east, and Ashley's distance is the diagonal. Using the Pythagorean Theorem we calculate the diagonal as √(12 + 12) = √2. So Daria walked 2 miles, and Ashley walked √2 miles. Therefore the difference is simply 2 – √2 miles.
Compare your answer with the correct one above
Which of the following sets of sides cannnot belong to a right triangle?
Which of the following sets of sides cannnot belong to a right triangle?
To answer this question without plugging all five answer choices in to the Pythagorean Theorem (which takes too long on the GRE), we can use special triangle formulas. Remember that 45-45-90 triangles have lengths of x, x, x√2. Similarly, 30-60-90 triangles have lengths x, x√3, 2x. We should also recall that 3,4,5 and 5,12,13 are special right triangles. Therefore the set of sides that doesn't fit any of these rules is 6, 7, 8.
To answer this question without plugging all five answer choices in to the Pythagorean Theorem (which takes too long on the GRE), we can use special triangle formulas. Remember that 45-45-90 triangles have lengths of x, x, x√2. Similarly, 30-60-90 triangles have lengths x, x√3, 2x. We should also recall that 3,4,5 and 5,12,13 are special right triangles. Therefore the set of sides that doesn't fit any of these rules is 6, 7, 8.
Compare your answer with the correct one above
Max starts at Point A and travels 6 miles north to Point B and then 4 miles east to Point C. What is the shortest distance from Point A to Point C?
Max starts at Point A and travels 6 miles north to Point B and then 4 miles east to Point C. What is the shortest distance from Point A to Point C?
This can be solved with the Pythagorean Theorem.
62 + 42 = _c_2
52 = _c_2
c = √52 = 2√13
This can be solved with the Pythagorean Theorem.
62 + 42 = _c_2
52 = _c_2
c = √52 = 2√13
Compare your answer with the correct one above
Which set of side lengths CANNOT correspond to a right triangle?
Which set of side lengths CANNOT correspond to a right triangle?
Because we are told this is a right triangle, we can use the Pythagorean Theorem, _a_2 + _b_2 = _c_2. You may also remember some of these as special right triangles that are good to memorize, such as 3, 4, 5.
Here, 6, 8, 11 will not be the sides to a right triangle because 62 + 82 = 102.
Because we are told this is a right triangle, we can use the Pythagorean Theorem, _a_2 + _b_2 = _c_2. You may also remember some of these as special right triangles that are good to memorize, such as 3, 4, 5.
Here, 6, 8, 11 will not be the sides to a right triangle because 62 + 82 = 102.
Compare your answer with the correct one above
Kathy and Jill are travelling from their home to the same destination. Kathy travels due east and then after travelling 6 miles turns and travels 8 miles due north. Jill travels directly from her home to the destination. How miles does Jill travel?
Kathy and Jill are travelling from their home to the same destination. Kathy travels due east and then after travelling 6 miles turns and travels 8 miles due north. Jill travels directly from her home to the destination. How miles does Jill travel?
Kathy's path traces the outline of a right triangle with legs of 6 and 8. By using the Pythagorean Theorem
miles
Kathy's path traces the outline of a right triangle with legs of 6 and 8. By using the Pythagorean Theorem
Compare your answer with the correct one above
Square 
is on the coordinate plane, and each side of the square is parallel to either the 
-axis or 
-axis. Point 
has coordinates 
and point 
has the coordinates 
.
Quantity A: 
Quantity B: The distance between points 
and 
Square
Quantity A:
Quantity B: The distance between points
To find the distance between points 
and 
, split the square into two 45-45-90 triangles and find the hypotenuse. The side ratio of the 45-45-90 triangle is 
, so if the sides have a length of 5, the hypotenuse must be 
.
To find the distance between points
Compare your answer with the correct one above
2 triangles are similar
Triangle 1 has sides 6, 8, 10
Triangle 2 has sides 5 , 3, x
find x
2 triangles are similar
Triangle 1 has sides 6, 8, 10
Triangle 2 has sides 5 , 3, x
find x
Draw the triangles
Triangle 1 is a 6,8,10 right triangle with 10 as the hypotenuse
Triangle 2: 3 is half of 6, 5 is half of 10; x must be half of 8
Draw the triangles
Triangle 1 is a 6,8,10 right triangle with 10 as the hypotenuse
Triangle 2: 3 is half of 6, 5 is half of 10; x must be half of 8
Compare your answer with the correct one above
Given the diagram, indicate if Quantity A is larger, Quantity B is larger, if they are equal, or if there is not enough information given to determine the relationship.
Quantity A: 
Quantity B: 7.5
Given the diagram, indicate if Quantity A is larger, Quantity B is larger, if they are equal, or if there is not enough information given to determine the relationship.
Quantity A:
Quantity B: 7.5
Since this is a 30-60-90 triangle, we know that the length of the side opposite the 60 degree angle is 
times the side opposite the 30 degree angle. Thus, 
, which is about 8.66. This is larger than 7.5.
Since this is a 30-60-90 triangle, we know that the length of the side opposite the 60 degree angle is
Compare your answer with the correct one above
A right triangle's perimeter is 
. The other two angles of the triangle are 30 degrees and 60 degrees.
Quantity A: The triangle's hypotenuse length
Quantity B: 2
A right triangle's perimeter is
Quantity A: The triangle's hypotenuse length
Quantity B: 2
The ratio of the sides of a 30-60-90 triangle is 
, with the hypotenuse being 
. Thus, the perimeter of this triangle would be 
. Since the triangle depicted in this problem has a perimeter of 
, 
must equal 1, which would make the hypotenuse equal to 2.
The ratio of the sides of a 30-60-90 triangle is
Compare your answer with the correct one above
If the shortest side of a right triangle has length 
and its hypotenuse has length 
, what is the length of the remaining side?
If the shortest side of a right triangle has length
Use the Pythagorean theorem, 
, with 
and 
, and solve for 
.
Rearrange to isolate 
:
Use FOIL to multiply out:
Distribute the minus sign to rewrite without parentheses:
Combine like terms:
Take the square root of both sides:
Use the Pythagorean theorem,
Rearrange to isolate
Use FOIL to multiply out:
Distribute the minus sign to rewrite without parentheses:
Combine like terms:
Take the square root of both sides:
Compare your answer with the correct one above