Acute / Obtuse Triangles - GRE Quantitative Reasoning
Card 0 of 14
In the figure above, what is the value of angle x?
In the figure above, what is the value of angle x?
To find the top inner angle, recognize that a straight line contains 180o; thus we can subtract 180 – 115 = 65o. Since we are given the other interior angle of 30 degrees, we can add the two we know: 65 + 30 = 95o.
180 - 95 = 85
To find the top inner angle, recognize that a straight line contains 180o; thus we can subtract 180 – 115 = 65o. Since we are given the other interior angle of 30 degrees, we can add the two we know: 65 + 30 = 95o.
180 - 95 = 85
Compare your answer with the correct one above
The three angles in a triangle measure 3_x_, 4_x_ + 10, and 8_x_ + 20. What is x?
The three angles in a triangle measure 3_x_, 4_x_ + 10, and 8_x_ + 20. What is x?
We know the angles in a triangle must add up to 180, so we can solve for x.
3_x_ + 4_x_ + 10 + 8_x_ + 20 = 180
15_x_ + 30 = 180
15_x_ = 150
x = 10
We know the angles in a triangle must add up to 180, so we can solve for x.
3_x_ + 4_x_ + 10 + 8_x_ + 20 = 180
15_x_ + 30 = 180
15_x_ = 150
x = 10
Compare your answer with the correct one above
In triangle ABC, AB=6, AC=3, and BC=4.
Quantity A Quantity B
angle C the sum of angle A and angle B
In triangle ABC, AB=6, AC=3, and BC=4.
Quantity A Quantity B
angle C the sum of angle A and angle B
The given triangle is obtuse. Thus, angle 
is greater than 90 degrees. A triangle has a sum of 180 degrees, so angle 
+ angle 
+ angle 
= 180. Since angle C is greater than 90 then angle 
+ angle 
must be less than 90 and it follows that Quantity A is greater.
The given triangle is obtuse. Thus, angle
Compare your answer with the correct one above
What is the area of a triangle with side lengths 18, 24, and 30?
What is the area of a triangle with side lengths 18, 24, and 30?
The question doesn't tell us if this is a right triangle, so we can't assume that it is. But there is a formula to find the area when we don't know the height: area = \[p(p – a)(p – b)(p – c)\]1/2, where a, b, and c are the side lengths and p is half of the perimeter. The perimeter is 18 + 24 + 30 = 72, so p = 72/2 = 36.
Then area = \[36(36 – 18)(36 – 24)(36 – 30)\]1/2 = \[36 * 12 * 6 * 18\]1/2 = 216.
The question doesn't tell us if this is a right triangle, so we can't assume that it is. But there is a formula to find the area when we don't know the height: area = \[p(p – a)(p – b)(p – c)\]1/2, where a, b, and c are the side lengths and p is half of the perimeter. The perimeter is 18 + 24 + 30 = 72, so p = 72/2 = 36.
Then area = \[36(36 – 18)(36 – 24)(36 – 30)\]1/2 = \[36 * 12 * 6 * 18\]1/2 = 216.
Compare your answer with the correct one above
You are asked which triangle is larger. You are only told that theyhave the same base length and that one contains at least one 3 inch side and the other contains at least one 4 inch side. Determine whether the left or right triangle is larger.
You are asked which triangle is larger. You are only told that theyhave the same base length and that one contains at least one 3 inch side and the other contains at least one 4 inch side. Determine whether the left or right triangle is larger.
Since we are told nothing about the angles we cannot assume that these are isosceles triangles and are open to possibilites such as that shown below in which the left side would be larger. If both were isosceles triangles then the right side would be larger.
Since we are told nothing about the angles we cannot assume that these are isosceles triangles and are open to possibilites such as that shown below in which the left side would be larger. If both were isosceles triangles then the right side would be larger.
Compare your answer with the correct one above
A triangle has sides 3, 5, and x. What can side x not be equal to?
A triangle has sides 3, 5, and x. What can side x not be equal to?
This question draws from the Third Side Rule of triangles. The length of any side of a triangle must be greater than the difference between the other sides and less than the sum of the other two sides.
This means that side x must be between 2 and 8 since the difference between 5 – 3 = 2 and the sum of 3 + 5 = 8.
Choices 3, 4, and 6 all fall within the range of 2 to 8, but choice 9 does not. The answer is 9.
This question draws from the Third Side Rule of triangles. The length of any side of a triangle must be greater than the difference between the other sides and less than the sum of the other two sides.
This means that side x must be between 2 and 8 since the difference between 5 – 3 = 2 and the sum of 3 + 5 = 8.
Choices 3, 4, and 6 all fall within the range of 2 to 8, but choice 9 does not. The answer is 9.
Compare your answer with the correct one above
Which of these side lengths cannot form a triangle?
Which of these side lengths cannot form a triangle?
Two sides of a triangle must add up to greater than the third side. 25, 37, 66 cannot be the lengths of the sides of a triangle as 25 + 37 < 66.
Two sides of a triangle must add up to greater than the third side. 25, 37, 66 cannot be the lengths of the sides of a triangle as 25 + 37 < 66.
Compare your answer with the correct one above
The sides of a triangle are 6, 12, and an integer x. How many possible values does x have?
The sides of a triangle are 6, 12, and an integer x. How many possible values does x have?
If two sides of a triangle are 6 and 12, the third must be greater than 12-6 and less than 12+6 since two sides cannot be summed to be greater than the third side in a triangle. There are 11 possible values for x: 7, 8, 9, 10,11, 12, 13, 14, 15, 16, 17.
If two sides of a triangle are 6 and 12, the third must be greater than 12-6 and less than 12+6 since two sides cannot be summed to be greater than the third side in a triangle. There are 11 possible values for x: 7, 8, 9, 10,11, 12, 13, 14, 15, 16, 17.
Compare your answer with the correct one above
Two sides of a triangle are 5 and 7. Which CANNOT be the length of the third side?
Two sides of a triangle are 5 and 7. Which CANNOT be the length of the third side?
12: The sum of two sides of a triangle must be greater than the third side. Therefore, the length of the third side would have to be less than 12 and greater than 2.
12: The sum of two sides of a triangle must be greater than the third side. Therefore, the length of the third side would have to be less than 12 and greater than 2.
Compare your answer with the correct one above
What is a possible value for the length of the missing side?
What is a possible value for the length of the missing side?
For a triangle where the length of two sides, 
and 
, is the only information known, the third side, 
, is limited in the following matter:
For the triangle given:
.
Both choices A and B satisfy this criteria.
For a triangle where the length of two sides,
For the triangle given:
Both choices A and B satisfy this criteria.
Compare your answer with the correct one above
A triangle has sides of lengths 
and 
Quantity A: The length of the missing side.
Quantity B: 
A triangle has sides of lengths
Quantity A: The length of the missing side.
Quantity B:
If two sides of a triangle are known and all angles are unknown, the length of the third side is limited by the difference and sum of the other two sides.
The missing side must be greater than 
.
Quantity A is greater.
If two sides of a triangle are known and all angles are unknown, the length of the third side is limited by the difference and sum of the other two sides.
The missing side must be greater than
Quantity A is greater.
Compare your answer with the correct one above
A triangle has sides 
and 
Quantity A: The length of the missing side.
Quantity B: 
A triangle has sides
Quantity A: The length of the missing side.
Quantity B:
If two sides of a triangle are known and the angles of the triangle are unknown, the length of the missing side is limited by the difference and sum of the other two sides.
For a triangle with sides 
and 
, there is no way a side could be 
.
Quantity B is greater.
If two sides of a triangle are known and the angles of the triangle are unknown, the length of the missing side is limited by the difference and sum of the other two sides.
For a triangle with sides
Quantity B is greater.
Compare your answer with the correct one above
The lengths of two sides of a triangle are 
and 
.
Quantity A: The length of the missing side.
Quantity B: 
The lengths of two sides of a triangle are
Quantity A: The length of the missing side.
Quantity B:
Seeing the sides 
and 
may bring to mind a 
triangle. However, we've been told nothing about the angles of the triangle. It could be right, or it could be obtuse or acute.
Since the angles are unknown, the side is bounded as follows:
There are plenty of potential lengths that fall above and below 
. The relationship cannot be determined.
Seeing the sides
Since the angles are unknown, the side is bounded as follows:
There are plenty of potential lengths that fall above and below
Compare your answer with the correct one above
The obtuse Isosceles triangle shown above has two sides with length 
and one side length 
. The length of side 
. The length of side 
. Find the perimeter of the triangle.
The obtuse Isosceles triangle shown above has two sides with length
To solve this problem, apply the formula: 
Side 
, side 
must equal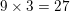 
Since this is an Isosceles triangle, there must be two sides with a length of 
.
Thus, plug in each side lengths value to find the solution:
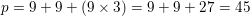
To solve this problem, apply the formula:
Side
Since this is an Isosceles triangle, there must be two sides with a length of
Thus, plug in each side lengths value to find the solution:
Compare your answer with the correct one above