Squares - GRE Quantitative Reasoning
Card 0 of 20
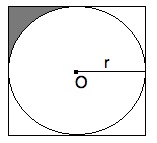
In order to solve this, we must first find the area of the containing square and then remove the inscribed circle. Once this is done, we need to divide our result by 4 in order to get the one-forth that is the one shaded region.
One side of the square will be equal to the circle's diameter (2r). Since r = 5, d = 10. Therefore, the area of the square is d2 = 102 = 100. The area of the circle is πr2 = 52π = 25π.
Therefore, the area of the four "corner regions" is equal to 100 - 25π. One of these is equal to (100 - 25π) / 4. Simplified, this is 25 - (25/4)π.
In order to solve this, we must first find the area of the containing square and then remove the inscribed circle. Once this is done, we need to divide our result by 4 in order to get the one-forth that is the one shaded region.
One side of the square will be equal to the circle's diameter (2r). Since r = 5, d = 10. Therefore, the area of the square is d2 = 102 = 100. The area of the circle is πr2 = 52π = 25π.
Therefore, the area of the four "corner regions" is equal to 100 - 25π. One of these is equal to (100 - 25π) / 4. Simplified, this is 25 - (25/4)π.
Compare your answer with the correct one above
Find the area of a square with a side length of 4.
Find the area of a square with a side length of 4.
All sides are equal in a square. To find the area of a square, multiply length times width. We know length = 4 but since all sides are equal, the width is also 4. 4 * 4 = 16.
All sides are equal in a square. To find the area of a square, multiply length times width. We know length = 4 but since all sides are equal, the width is also 4. 4 * 4 = 16.
Compare your answer with the correct one above
To compare, first calculate the area of figure 1. Since it shares dimensions with the semi-circle, we will put all our variables in terms of the radius of that semi-circle:
A1 = (2r)2 + πr2/2 = 4r2 + πr2/2 = r2(4 + π)/2
If we double r, we get:
A2 = (2 * 2r)2 + π(2r)2/2 = 16r2 + π4r2/2 = 4r2(4 + π)/2
This means that the new figure is 4x the size of the original. This is an increase of 300%.
To compare, first calculate the area of figure 1. Since it shares dimensions with the semi-circle, we will put all our variables in terms of the radius of that semi-circle:
A1 = (2r)2 + πr2/2 = 4r2 + πr2/2 = r2(4 + π)/2
If we double r, we get:
A2 = (2 * 2r)2 + π(2r)2/2 = 16r2 + π4r2/2 = 4r2(4 + π)/2
This means that the new figure is 4x the size of the original. This is an increase of 300%.
Compare your answer with the correct one above
100 cm = 1 m
Quantity A: The area of a square with side 1 m
Quantity B: One hundred times the area of a square with side 1 cm
100 cm = 1 m
Quantity A: The area of a square with side 1 m
Quantity B: One hundred times the area of a square with side 1 cm
The obvious answer for this problem is that they are equal. Remember quantitative comparisons are often tricky and require you to check your initial inclination. If 1 m equals 100 cm then a square with side 1 m (100 cm) has an area of 100 cm x 100 cm or 10,000 cm2. The area of a square with a 1 cm side is 1 cm x 1 cm or 1 cm2. One hundred times 1 cm2 is 100 cm2. 10,000 cm2 is larger than 100 cm2 so Quantity A is greater.
The obvious answer for this problem is that they are equal. Remember quantitative comparisons are often tricky and require you to check your initial inclination. If 1 m equals 100 cm then a square with side 1 m (100 cm) has an area of 100 cm x 100 cm or 10,000 cm2. The area of a square with a 1 cm side is 1 cm x 1 cm or 1 cm2. One hundred times 1 cm2 is 100 cm2. 10,000 cm2 is larger than 100 cm2 so Quantity A is greater.
Compare your answer with the correct one above
A square is inscribed in a circle. The diameter of the circle is 10 feet. What is the area of the square?
A square is inscribed in a circle. The diameter of the circle is 10 feet. What is the area of the square?
Since the diameter of the circle is 10, we know the radius of the circle is 5 feet. We can then draw radii that go from the center to two consecutive corners of the square. These radii are both 5 feet, and form a 90 degree angle (since they are diagonals of a square). Thus, with the enclosed side of the square they form a 45-45-90 triangle. Thus, the side of the square must be  (this can also be found with the Pythagorean theorem). Then, the area of the square is
(this can also be found with the Pythagorean theorem). Then, the area of the square is

Since the diameter of the circle is 10, we know the radius of the circle is 5 feet. We can then draw radii that go from the center to two consecutive corners of the square. These radii are both 5 feet, and form a 90 degree angle (since they are diagonals of a square). Thus, with the enclosed side of the square they form a 45-45-90 triangle. Thus, the side of the square must be 
Compare your answer with the correct one above

In the figure above, a square is inscribed in a circle with a diameter of 5 cm.
What is the area of the square?

In the figure above, a square is inscribed in a circle with a diameter of 5 cm.
What is the area of the square?
The diameter of the circle and the sides of the square form a 45-45-90 triangle. Since the hypotenuse is 5 cm, then a leg of the triangle (a side of the square) is  .
.
The area of the square is then  .
.
The diameter of the circle and the sides of the square form a 45-45-90 triangle. Since the hypotenuse is 5 cm, then a leg of the triangle (a side of the square) is 
The area of the square is then 
Compare your answer with the correct one above
Square  is on a coordinate plane, and each side of the square is parallel to either the
is on a coordinate plane, and each side of the square is parallel to either the  -axis or
-axis or  -axis. Point
-axis. Point  has the coordinate
has the coordinate  and Point
and Point  has the coordinate
has the coordinate 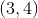 .
.
Quantity A: The area of square 
Quantity B: 24
Square 





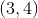
Quantity A: The area of square
Quantity B: 24
If you draw points  and
and  on the coordinate plane, you know that they are opposite ends of the square, since the sides are parallel to the axes. This means that the squares have sides with lengths of 5, making the area 25.
on the coordinate plane, you know that they are opposite ends of the square, since the sides are parallel to the axes. This means that the squares have sides with lengths of 5, making the area 25.
If you draw points 

Compare your answer with the correct one above
If a square has a side length of 4, how long is the diagonal of the square?
If a square has a side length of 4, how long is the diagonal of the square?
A diagonal divides a square into two 45-45-90 triangles, which have lengths adhering to the ratio of x: x: x√2. Therefore, 4√2 is the correct answer as the diagonal represents the hypotenuse of the triangle. the Pythagorean theorem can also be used: 42+ 42 = c2.
A diagonal divides a square into two 45-45-90 triangles, which have lengths adhering to the ratio of x: x: x√2. Therefore, 4√2 is the correct answer as the diagonal represents the hypotenuse of the triangle. the Pythagorean theorem can also be used: 42+ 42 = c2.
Compare your answer with the correct one above
If a square has a side length of √2, how long is the diagonal of the square?
If a square has a side length of √2, how long is the diagonal of the square?
A diagonal divides a square into two 45-45-90 triangles, which have lengths adhering to the ratio of x: x: x√2. Therefore, 2 is the correct answer as the diagonal represents the hypotenuse of the triangle. the Pythagorean theorem can also be used: √22+ √22 = c2.
A diagonal divides a square into two 45-45-90 triangles, which have lengths adhering to the ratio of x: x: x√2. Therefore, 2 is the correct answer as the diagonal represents the hypotenuse of the triangle. the Pythagorean theorem can also be used: √22+ √22 = c2.
Compare your answer with the correct one above
A square has a side of length 5. What is the length of its diagonal?
A square has a side of length 5. What is the length of its diagonal?
The diagonal separates the square into two 45-45-90 right triangles. The problem can be solved by using the Pythagorean Theorem, _a_2 + _b_2 = _c_2. It can also be solved by recognizing the 45-45-90 special triangles, which have side ratios of x : x : x√2.
The diagonal separates the square into two 45-45-90 right triangles. The problem can be solved by using the Pythagorean Theorem, _a_2 + _b_2 = _c_2. It can also be solved by recognizing the 45-45-90 special triangles, which have side ratios of x : x : x√2.
Compare your answer with the correct one above
A square with width of  is inscribed in a circle. What is the total area inside the circle?
is inscribed in a circle. What is the total area inside the circle?
A square with width of 
We know that each side of the square is 6, so use the Pythagorean Theorem to solve for the diagonal of the square. The diagonal of the square is also the diameter of the circle.





Therefore the radius must be 
Now let's find the area inside the circle using the radius.



 meters2
meters2
We know that each side of the square is 6, so use the Pythagorean Theorem to solve for the diagonal of the square. The diagonal of the square is also the diameter of the circle.
Therefore the radius must be
Now let's find the area inside the circle using the radius.

Compare your answer with the correct one above
Quantity A:
The diagonal of a square with a side-length of  .
.
Quantity B:
The side-length of a square with a diagonal of  .
.
Quantity A:
The diagonal of a square with a side-length of 
Quantity B:
The side-length of a square with a diagonal of 
Quantity A: The diagonal of a square with a side-length of 7.
Quantity B: The side-length of a square with a diagonal of 14.
Both quantities can be determined, so can the relationship.
Quantity A:
To determine the diagonal of a square, it's important to remember that a diagonal directly bisects a square from corner to corner. In other words, it bisects the corners, creating two triangles with 45:45:90 proportions, with the diagonal serving as the hypotenuses . If you remember your special triangles, then the side-side-hypotenuse measurements have a ratio of  .
.
In Quantity A, the side-length is 7. Following the proportion:

The diagonal equals  .
.
Quantity B:
We can use the same ratio to figure out quantity B by substituting x for the unknown side-length quantity, which looks like this:

To find x in this ratio, just isolate x in the hypotenuse:

Divide by 

Now, how does Quantity A and Quantity B match up?


On the surface, it looks like the two quanties are equal. But how do we prove it? Well, we know that  . Therefore, we know that:
. Therefore, we know that:

Divide both sides by 

Therefore, both quantities are equal.
Quantity A: The diagonal of a square with a side-length of 7.
Quantity B: The side-length of a square with a diagonal of 14.
Both quantities can be determined, so can the relationship.
Quantity A:
To determine the diagonal of a square, it's important to remember that a diagonal directly bisects a square from corner to corner. In other words, it bisects the corners, creating two triangles with 45:45:90 proportions, with the diagonal serving as the hypotenuses . If you remember your special triangles, then the side-side-hypotenuse measurements have a ratio of 
In Quantity A, the side-length is 7. Following the proportion:
The diagonal equals 
Quantity B:
We can use the same ratio to figure out quantity B by substituting x for the unknown side-length quantity, which looks like this:
To find x in this ratio, just isolate x in the hypotenuse:
Divide by
Now, how does Quantity A and Quantity B match up?
On the surface, it looks like the two quanties are equal. But how do we prove it? Well, we know that 
Divide both sides by
Therefore, both quantities are equal.
Compare your answer with the correct one above
Quantity A:
The side-length of a square with a perimeter of  .
.
Quantity B:
The side-length of a square with an area of  .
.
Quantity A:
The side-length of a square with a perimeter of 
Quantity B:
The side-length of a square with an area of 
The first step to a quantitative comparison is to determine whether it can be solved at all with the given knowledge. Since all you need to find the side-length of a square is the perimeter, the area, OR the diagonal and we have one of each for these two quantities, this relationship can be determined. Thus, "the relationship cannot be determined" is out.
Now, to solve both quantities. Quantity A can be solved by translating the perimeter into side lengths: the formula for the perimeter of a square is  , with
, with  being the side-length, so you just need to divide the perimeter by four.
being the side-length, so you just need to divide the perimeter by four.


Thus, quantity A is  .
.
Quantity B can be solved by translating the area into side lengths: the formula for the area of a square is  , or
, or  , with
, with  being the side-length, so you just need to find the square root of the area.
being the side-length, so you just need to find the square root of the area.


Thus, quantity B is roughly  .
.
Therefore quantity A is greater.
The first step to a quantitative comparison is to determine whether it can be solved at all with the given knowledge. Since all you need to find the side-length of a square is the perimeter, the area, OR the diagonal and we have one of each for these two quantities, this relationship can be determined. Thus, "the relationship cannot be determined" is out.
Now, to solve both quantities. Quantity A can be solved by translating the perimeter into side lengths: the formula for the perimeter of a square is 

Thus, quantity A is 
Quantity B can be solved by translating the area into side lengths: the formula for the area of a square is 


Thus, quantity B is roughly 
Therefore quantity A is greater.
Compare your answer with the correct one above

Circle  has a center in the center of Square
has a center in the center of Square  .
.
If the area of Circle  is
is  , what is the length of
, what is the length of  ?
?

Circle 

If the area of Circle 


If the area of Circle  is
is  , we know that the area can be computed using the standard area formula:
, we know that the area can be computed using the standard area formula:
 , using
, using  for
for 

Simplifying, we get:

We know that  must be less than
must be less than  . By choosing
. By choosing  for
for  , we find out that this is the radius of our circle. Thus, we know that the diameter of the circle is double this, or
, we find out that this is the radius of our circle. Thus, we know that the diameter of the circle is double this, or  . Now, consider the following diagram:
. Now, consider the following diagram:

Notice that the diameter is the same length as a side of the square. Thus,  is equal to
is equal to  .
.
If the area of Circle 



Simplifying, we get:
We know that 





Notice that the diameter is the same length as a side of the square. Thus, 

Compare your answer with the correct one above

Circle  has a center in the center of square
has a center in the center of square  .
.
The line segment marked with length 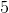 lies on the diagonal of the square
lies on the diagonal of the square  .
.
What is the length of side  ?
?

Circle 

The line segment marked with length 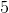

What is the length of side 
You can further fill in your diagram as follows:

Now, we know that the triangle  is a
is a  triangle. We also know that the length of
triangle. We also know that the length of  and
and  must also be equal to the diameter of the circle. (The diameter of the circle will run across the circle horizontally if you draw it that way. This will provide you with a complete side length.) Now, we know that the ratio of the hypotenuse of
must also be equal to the diameter of the circle. (The diameter of the circle will run across the circle horizontally if you draw it that way. This will provide you with a complete side length.) Now, we know that the ratio of the hypotenuse of  to the side must be the same as:
to the side must be the same as:

For our data, that means:

Simplifying, we know:



Now, make both sides reciprocals:

Finally, solve:

Recall, this is both the length of the side and the diameter of the circle. Hence, you have your answer.
You can further fill in your diagram as follows:

Now, we know that the triangle 




For our data, that means:
Simplifying, we know:
Now, make both sides reciprocals:
Finally, solve:
Recall, this is both the length of the side and the diameter of the circle. Hence, you have your answer.
Compare your answer with the correct one above
We know that our area can be represented by the following equation:

Instead of solving the algebra, you should immediately note several things. 16 = 42 and 4 = 22. If the side of the square is 4, then s = 4 would work out as:

which is just what we need.
With s = 4, we know that 3 sides of our figure will have a perimeter of 12. The remaining semicircle will be one half of the circumference of a circle with diameter of 4; therefore it will be 0.5 * 4 * π or 2π.
Therefore, the outer perimeter of our figure is 12 + 2π.
We know that our area can be represented by the following equation:
Instead of solving the algebra, you should immediately note several things. 16 = 42 and 4 = 22. If the side of the square is 4, then s = 4 would work out as:
which is just what we need.
With s = 4, we know that 3 sides of our figure will have a perimeter of 12. The remaining semicircle will be one half of the circumference of a circle with diameter of 4; therefore it will be 0.5 * 4 * π or 2π.
Therefore, the outer perimeter of our figure is 12 + 2π.
Compare your answer with the correct one above
What is the perimeter of a square that has an area of 81?
What is the perimeter of a square that has an area of 81?
36
A square has four equal sides and its area = side2. Therefore, you can find the side length by taking the square root of the area √81 = 9. Then, find the perimeter by multiplying the side length by 4:
4 * 9 = 36
36
A square has four equal sides and its area = side2. Therefore, you can find the side length by taking the square root of the area √81 = 9. Then, find the perimeter by multiplying the side length by 4:
4 * 9 = 36
Compare your answer with the correct one above

The radius of the circle is 2 inches. What is the perimeter of the inscribed square?

The radius of the circle is 2 inches. What is the perimeter of the inscribed square?
The center of an inscribed square lies on the center of the circle. Thus, the line joining the center to a vertex of the square is also the radius. If we join the center with two adjacent vertices we can create a 45-45-90 right isosceles triangle, where the diagonal of the square is the hypotenuse. Since the radius is 2, the hypotenuse (a side of the square) must be  .
.
Finally, the perimeter of a square is  .
.
The center of an inscribed square lies on the center of the circle. Thus, the line joining the center to a vertex of the square is also the radius. If we join the center with two adjacent vertices we can create a 45-45-90 right isosceles triangle, where the diagonal of the square is the hypotenuse. Since the radius is 2, the hypotenuse (a side of the square) must be 
Finally, the perimeter of a square is 
Compare your answer with the correct one above
A square table has an area of  square centimeters and a perimeter of
square centimeters and a perimeter of  centimeters.
centimeters.
If  , what is the perimeter of the square?
, what is the perimeter of the square?
A square table has an area of 

If 
We start by writing the equations for the area and perimeter in terms of a side of length s.


Then, substitute both of these expressions into the given equation to solve for side length.




Finally, since four sides make up the perimeter, we substitue s back into our perimeter equation and solve for P.

We start by writing the equations for the area and perimeter in terms of a side of length s.
Then, substitute both of these expressions into the given equation to solve for side length.
Finally, since four sides make up the perimeter, we substitue s back into our perimeter equation and solve for P.
Compare your answer with the correct one above
The diagonal of square  is
is  feet. Approximately how long in inches is the perimeter of square
feet. Approximately how long in inches is the perimeter of square  ?
?
The diagonal of square 


First we must convert to inches.

The diagonal of a square divides the square into two isosceles-right triangles. Using the Pythagorean Theorem, we know that  , where x is equal to the length of one side of the square.
, where x is equal to the length of one side of the square.
This gives us  .
.
Therefore, the perimeter of square  is equal to
is equal to  .
.
First we must convert to inches.
The diagonal of a square divides the square into two isosceles-right triangles. Using the Pythagorean Theorem, we know that 
This gives us 
Therefore, the perimeter of square 

Compare your answer with the correct one above