Rectangles - GRE Quantitative Reasoning
Card 0 of 16
The perimeter of a rectangle is 14, and the diagonal connecting two vertices is 5.
Quantity A: 13
Quantity B: The area of the rectangle
The perimeter of a rectangle is 14, and the diagonal connecting two vertices is 5.
Quantity A: 13
Quantity B: The area of the rectangle
One potentially helpful first step is to draw the rectangle described in the problem statement:

After that, it's a matter of using the other information given. The perimeter is given as 14, and can be written in terms of the length and width of the rectangle:

Furthermore, notice that the diagonal forms the hypotenuse of a right triangle. The Pythagorean Theorem may be applied:
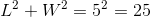
This provides two equations and two unknowns. Redefining the first equation to isolate  gives:
gives:

Plugging this into the second equation in turn gives:
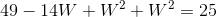
Which can be reduced to:
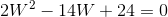
or

Note that there are two possibile values for  ; 3 or 4. The one chosen is irrelevant. Choosing a value 3, it is possible to then find a value for
; 3 or 4. The one chosen is irrelevant. Choosing a value 3, it is possible to then find a value for 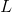 :
:
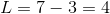
This in turn allows for the definition of the rectangle's area:

So Quantity B is 12, which is less than Quantity A.
One potentially helpful first step is to draw the rectangle described in the problem statement:

After that, it's a matter of using the other information given. The perimeter is given as 14, and can be written in terms of the length and width of the rectangle:
Furthermore, notice that the diagonal forms the hypotenuse of a right triangle. The Pythagorean Theorem may be applied:
This provides two equations and two unknowns. Redefining the first equation to isolate 
Plugging this into the second equation in turn gives:
Which can be reduced to:
or
Note that there are two possibile values for 
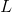
This in turn allows for the definition of the rectangle's area:
So Quantity B is 12, which is less than Quantity A.
Compare your answer with the correct one above
One rectangle has a height of  and a width of
and a width of  . Which of the following is a possible perimeter of a similar rectangle, having one side that is
. Which of the following is a possible perimeter of a similar rectangle, having one side that is  ?
?
One rectangle has a height of 


Based on the information given, we know that  could be either the longer or the shorter side of the similar rectangle. Similar rectangles have proportional sides. We might need to test both, but let us begin with the easier proportion, namely:
could be either the longer or the shorter side of the similar rectangle. Similar rectangles have proportional sides. We might need to test both, but let us begin with the easier proportion, namely:
 as
as 
For this proportion, you really do not even need fractions. You know that  must be
must be  .
.
This means that the figure would have a perimeter of 
Luckily, this is one of the answers!
Based on the information given, we know that 

For this proportion, you really do not even need fractions. You know that 

This means that the figure would have a perimeter of
Luckily, this is one of the answers!
Compare your answer with the correct one above
One rectangle has sides of  and
and  . Which of the following pairs could be the sides of a rectangle similar to this one?
. Which of the following pairs could be the sides of a rectangle similar to this one?
One rectangle has sides of 

For this problem, you need to find the pair of sides that would reduce to the same ratio as the original set of sides. This is a little tricky at first, but consider the set:
 and
and 
For this, you have:

Now, if you factor out  , you have:
, you have:

Thus, the proportions are the same, meaning that the two rectangles would be similar.
For this problem, you need to find the pair of sides that would reduce to the same ratio as the original set of sides. This is a little tricky at first, but consider the set:

For this, you have:
Now, if you factor out 
Thus, the proportions are the same, meaning that the two rectangles would be similar.
Compare your answer with the correct one above
If a rectangle's width is increased by 20%, and its length is decreased by 20%, which statement most accurately reflects the rectangle's change in area?
If a rectangle's width is increased by 20%, and its length is decreased by 20%, which statement most accurately reflects the rectangle's change in area?
If l x w = A, then we will call the new area B. B results when l has been decreased by 20% and w has been increased by 20%: in other words, 80% of l and 120% of w.
This is expressed as (0.8) l * (1.2) w = B
The simplest way to determine the result is to create rectangles with actual integers and see what happens. Let's say our first rectangle is a square 10 units by 10 units.
10 * 10 = 100 for our A.
Plugging these numbers into our new equation gives us:
(0.8)10 * (1.2)10 = 96.
So the final step is to compare the areas. Because we used a 10 x 10 rectangle as our example, this step will be easy, since 100% = 100.
96/100 = 0.96
0.96 * 100 = 96%
Which reflects a 4% reduction in the size of the rectangle.
Any other length and width used for this rectangle will result in a 4% reduction in size when the above parameters are applied.
If l x w = A, then we will call the new area B. B results when l has been decreased by 20% and w has been increased by 20%: in other words, 80% of l and 120% of w.
This is expressed as (0.8) l * (1.2) w = B
The simplest way to determine the result is to create rectangles with actual integers and see what happens. Let's say our first rectangle is a square 10 units by 10 units.
10 * 10 = 100 for our A.
Plugging these numbers into our new equation gives us:
(0.8)10 * (1.2)10 = 96.
So the final step is to compare the areas. Because we used a 10 x 10 rectangle as our example, this step will be easy, since 100% = 100.
96/100 = 0.96
0.96 * 100 = 96%
Which reflects a 4% reduction in the size of the rectangle.
Any other length and width used for this rectangle will result in a 4% reduction in size when the above parameters are applied.
Compare your answer with the correct one above
Amy is building a rectangular patio in her backyard. She plans on making the patio 8 feet wide by 12 feet long. The rectangular bricks she is using are 6 inches long and 4 inches wide. How many bricks will Amy need to build her patio?
Amy is building a rectangular patio in her backyard. She plans on making the patio 8 feet wide by 12 feet long. The rectangular bricks she is using are 6 inches long and 4 inches wide. How many bricks will Amy need to build her patio?
Because Amy is building her patio in a rectangle, and the bricks are rectangular, the simplest way to find this solution is to determine how many bricks long and how many bricks wide her patio will be.
To do this, begin by converting the patio's dimensions into inches, since the bricks Amy is using are measured in inches.
Length:
12 feet * 12 inches in a foot = 144 inches long.
Width:
8 feet * 12 inches in a foot = 96 inches wide.
Now, all that's left to do is figure out how many bricks will fit in these spaces. Let's be intuitive and assume the long sides of the bricks will align with the long sides of the patio.
144 inches long / bricks that are 6 inches long = 24 bricks long
Amy will need columns of 24 bricks to cover the length of her patio. Now, for the width.
96 inches wide / bricks that are 4 inches wide = 24 bricks wide
Amy will need rows of 24 bricks to cover the width of her patio.
To determine how many bricks Amy will need in total, the last step is to multiply how many rows of bricks she will need by how many columns.
24 bricks to a row * 24 bricks to a column = 576
Amy needs 576 bricks to build her patio.
Because Amy is building her patio in a rectangle, and the bricks are rectangular, the simplest way to find this solution is to determine how many bricks long and how many bricks wide her patio will be.
To do this, begin by converting the patio's dimensions into inches, since the bricks Amy is using are measured in inches.
Length:
12 feet * 12 inches in a foot = 144 inches long.
Width:
8 feet * 12 inches in a foot = 96 inches wide.
Now, all that's left to do is figure out how many bricks will fit in these spaces. Let's be intuitive and assume the long sides of the bricks will align with the long sides of the patio.
144 inches long / bricks that are 6 inches long = 24 bricks long
Amy will need columns of 24 bricks to cover the length of her patio. Now, for the width.
96 inches wide / bricks that are 4 inches wide = 24 bricks wide
Amy will need rows of 24 bricks to cover the width of her patio.
To determine how many bricks Amy will need in total, the last step is to multiply how many rows of bricks she will need by how many columns.
24 bricks to a row * 24 bricks to a column = 576
Amy needs 576 bricks to build her patio.
Compare your answer with the correct one above
Rectangle  has a length of 20 inches and a width of 3 inches. Rectangle
has a length of 20 inches and a width of 3 inches. Rectangle  has a length of 9 inches and a width of 10 inches. By what number must the area of rectangle
has a length of 9 inches and a width of 10 inches. By what number must the area of rectangle  be multiplied by to equal the area of rectangle
be multiplied by to equal the area of rectangle  ?
?
Rectangle 



Area of rectangle  is
is  .
.
Area of rectangle  is
is 


Area of rectangle 

Area of rectangle 
Compare your answer with the correct one above
Quantity A: The area of a rectangle with a perimeter of 40
Quantity B: The area of a triangle with a perimeter of 40
Quantity A: The area of a rectangle with a perimeter of 40
Quantity B: The area of a triangle with a perimeter of 40
The area of the two shapes depends on their dimensions, which can vary greatly among different combinations. A rectangle with a perimeter of 40 could have dimensions of  (smaller area) or
(smaller area) or  (larger area), for instance. Similarly, a triangle could have sides of 10--11--19 (smaller area) or 13--13--14 (larger area). Thus, the relationship cannot be determined without more specific details.
(larger area), for instance. Similarly, a triangle could have sides of 10--11--19 (smaller area) or 13--13--14 (larger area). Thus, the relationship cannot be determined without more specific details.
The area of the two shapes depends on their dimensions, which can vary greatly among different combinations. A rectangle with a perimeter of 40 could have dimensions of 

Compare your answer with the correct one above
The perimeter of a rectangle is  . One side is
. One side is  . What is the area of this rectangle?
. What is the area of this rectangle?
The perimeter of a rectangle is 

Recall that perimeter is defined as:

For our data, this is:

Solve for  :
:


Therefore, 
This means that the area of the rectangle is equal to:

Recall that perimeter is defined as:
For our data, this is:
Solve for 
Therefore,
This means that the area of the rectangle is equal to:
Compare your answer with the correct one above
Given Rectangle ABCD.
Quantity A: The length of diagonal AC times the length of diagonal BD
Quantity B: The square of half of ABCD's perimeter
Given Rectangle ABCD.
Quantity A: The length of diagonal AC times the length of diagonal BD
Quantity B: The square of half of ABCD's perimeter
Suppose ABCD has sides a and b.
The length of one of ABCD's diagonals is given by a2+ b2 = c2, where c is one of the diagonals.
Note that both diagonals are of the same length.
Quantity A: The length of diagonal AC times the length of diagonal BD
This is c * c = c2.
Quantity A = c2 = a2+ b2
Now for Quantity B, remember that the perimeter of a rectangle with sides a and b is Perimeter = 2(a + b).
Half of Perimeter = (a + b)
Square Half of Perimeter = (a + b)2
Use FOIL: (a + b)2 = a2+ 2ab + b2
Quantity B = (a + b)2 = a2+ 2ab + b2
The question is asking us to compare a2+ b2 with a2+ 2ab + b2.
Note that as long as a and b are positive numbers (in this case a and b are dimensions of a rectangle, so they must be positive), the second quantity will be greater.
Suppose ABCD has sides a and b.
The length of one of ABCD's diagonals is given by a2+ b2 = c2, where c is one of the diagonals.
Note that both diagonals are of the same length.
Quantity A: The length of diagonal AC times the length of diagonal BD
This is c * c = c2.
Quantity A = c2 = a2+ b2
Now for Quantity B, remember that the perimeter of a rectangle with sides a and b is Perimeter = 2(a + b).
Half of Perimeter = (a + b)
Square Half of Perimeter = (a + b)2
Use FOIL: (a + b)2 = a2+ 2ab + b2
Quantity B = (a + b)2 = a2+ 2ab + b2
The question is asking us to compare a2+ b2 with a2+ 2ab + b2.
Note that as long as a and b are positive numbers (in this case a and b are dimensions of a rectangle, so they must be positive), the second quantity will be greater.
Compare your answer with the correct one above
If rectangle  has a perimeter of
has a perimeter of  , and the longer edge is
, and the longer edge is  times longer than the shorter edge, then how long is the diagonal
times longer than the shorter edge, then how long is the diagonal  ?
?
If rectangle 



Lets call our longer side L and our shorter side W.
If the perimeter is equal to 68, then
 .
.
We also have that
 .
.
If we then plug this into our equation for perimeter, we get  .
.
Therefore,  and
and  . Using the Pythagorean Theorem, we have
. Using the Pythagorean Theorem, we have  so
so  .
.
Lets call our longer side L and our shorter side W.
If the perimeter is equal to 68, then

We also have that

If we then plug this into our equation for perimeter, we get 
Therefore, 



Compare your answer with the correct one above
A rectangle has an area of 48 and a perimeter of 28. What are its dimensions?
A rectangle has an area of 48 and a perimeter of 28. What are its dimensions?
We can set up our data into the following two equations:
(Area) LH = 48
(Perimeter) 2L + 2H = 28
Solve the area equation for one of the two variables (here, length): L = 48 / H
Place that value for L into ever place you find L in the perimeter equation: 2(48 / H) + 2H = 28; then simplify:
96/H + 2H = 28
Multiply through by H: 96 + 2H2 = 28H
Get everything on the same side of the equals sign: 2H2 - 28H + 96 = 0
Divide out the common 2: H2 - 14H + 48 = 0
Factor: (H - 6) (H - 8) = 0
Either of these multiples can be 0, therefore, consider each one separately:
H - 6 = 0; H = 6
H - 8 = 0; H = 8
Because this is a rectangle, these two dimensions are the height and width. If you choose 6 for the "height" the other perpendicular dimension would be 8 and vice-versa. Therefore, the dimensions are 6 x 8.
We can set up our data into the following two equations:
(Area) LH = 48
(Perimeter) 2L + 2H = 28
Solve the area equation for one of the two variables (here, length): L = 48 / H
Place that value for L into ever place you find L in the perimeter equation: 2(48 / H) + 2H = 28; then simplify:
96/H + 2H = 28
Multiply through by H: 96 + 2H2 = 28H
Get everything on the same side of the equals sign: 2H2 - 28H + 96 = 0
Divide out the common 2: H2 - 14H + 48 = 0
Factor: (H - 6) (H - 8) = 0
Either of these multiples can be 0, therefore, consider each one separately:
H - 6 = 0; H = 6
H - 8 = 0; H = 8
Because this is a rectangle, these two dimensions are the height and width. If you choose 6 for the "height" the other perpendicular dimension would be 8 and vice-versa. Therefore, the dimensions are 6 x 8.
Compare your answer with the correct one above
The length of a rectangle is three times its width, and the perimeter is  . What is the width of the rectangle?
. What is the width of the rectangle?
The length of a rectangle is three times its width, and the perimeter is 
For any rectangle, 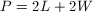 , where
, where  ,
,  , and
, and  .
.
In this problem, we are given that  (length is three times the width), so replace
(length is three times the width), so replace  in the perimeter equation with
in the perimeter equation with 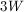 :
: 
Plug in our value for the perimeter, 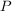 :
:

Simplify:
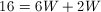


For any rectangle, 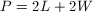



In this problem, we are given that 

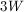
Plug in our value for the perimeter, 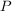
Simplify:
Compare your answer with the correct one above
The area of a rectangle is  . Its perimeter is
. Its perimeter is  . What is the length of its shorter side?
. What is the length of its shorter side?
The area of a rectangle is 

We know that the following two equations hold for rectangles. For area:

For perimeter:

Now, for our data, we know:


Now, solve the first equation for one of the variables:

Now, substitute this value into the second equation:

Solve for  :
:

Multiply both sides by  :
:

Solve as a quadratic. Divide through by  :
:

Now, get the equation into standard form:

Factor this:

This means that 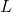 (or
(or  ) would equal either
) would equal either  or
or 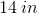 . Therefore, your answer is
. Therefore, your answer is  .
.
We know that the following two equations hold for rectangles. For area:
For perimeter:
Now, for our data, we know:
Now, solve the first equation for one of the variables:
Now, substitute this value into the second equation:
Solve for 
Multiply both sides by 
Solve as a quadratic. Divide through by 
Now, get the equation into standard form:
Factor this:
This means that 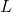


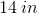

Compare your answer with the correct one above
Quantity A
The perimeter of a square with a diagonal of 12 inches.
Quantity B
The perimeter of a rectangle with a diagonal of 10 inches and longer sides that are three times the length of its shorter sides.
Quantity A
The perimeter of a square with a diagonal of 12 inches.
Quantity B
The perimeter of a rectangle with a diagonal of 10 inches and longer sides that are three times the length of its shorter sides.
The diagonal of a square creates a 45-45-90 triangle; therefore, considering x as the value for the sides of the square in A, set up the ratio: 1/√2 = x/12 → x = 12/√2
Simplify the square root out of the denominator: x = (12√2)/2 = 6√2. The perimeter is equal to 4x; therefore, quantity A is 24√2.
Use the Pythagorean Theorem for B. We know that one side of the triangle is x and the other must be 3x. Furthermore, we know the hypotenuse is 10; therefore:
x2 + (3x)2 = 102 → x2 + 9x2 = 100 → 10x2 = 100 → x2 = 10 → x = √10.
Transform the √10 into √2 * √5 ; therefore, x = √2 * √5 . The perimeter of the rectangle will equal 3x + 3x + x + x = 8x = 8√2 * √5 .
Compare these two values. Quantity A has a coefficient of 24 in for its √2 . Quantity B has a coefficient of 8√5, which must be smaller than 24, because 8 * 3 = 24, but √5 is less than 3 (which would be √9 ); therefore, A is larger.
The diagonal of a square creates a 45-45-90 triangle; therefore, considering x as the value for the sides of the square in A, set up the ratio: 1/√2 = x/12 → x = 12/√2
Simplify the square root out of the denominator: x = (12√2)/2 = 6√2. The perimeter is equal to 4x; therefore, quantity A is 24√2.
Use the Pythagorean Theorem for B. We know that one side of the triangle is x and the other must be 3x. Furthermore, we know the hypotenuse is 10; therefore:
x2 + (3x)2 = 102 → x2 + 9x2 = 100 → 10x2 = 100 → x2 = 10 → x = √10.
Transform the √10 into √2 * √5 ; therefore, x = √2 * √5 . The perimeter of the rectangle will equal 3x + 3x + x + x = 8x = 8√2 * √5 .
Compare these two values. Quantity A has a coefficient of 24 in for its √2 . Quantity B has a coefficient of 8√5, which must be smaller than 24, because 8 * 3 = 24, but √5 is less than 3 (which would be √9 ); therefore, A is larger.
Compare your answer with the correct one above
A rectangle has a length that is twice that of its height. If the perimeter of that rectangle is  , what is its area?
, what is its area?
A rectangle has a length that is twice that of its height. If the perimeter of that rectangle is 
Based on our first sentence, we know:

The second sentence means:
 , which is the same as:
, which is the same as:

Now, we can replace  with
with  in the second equation:
in the second equation:




Therefore, 
Now, this means that:

If these are our values, then the area of the rectangle is:

Based on our first sentence, we know:
The second sentence means:

Now, we can replace 

Therefore,
Now, this means that:
If these are our values, then the area of the rectangle is:
Compare your answer with the correct one above
A rectangle with an area of 64 square units is one-fourth as wide as it is long. What is the perimeter of the rectangle?
A rectangle with an area of 64 square units is one-fourth as wide as it is long. What is the perimeter of the rectangle?
Begin by setting up a ratio of width to length for the rectangle. We know that the width is one-fourth the length, therefore
 .
.
Now, we can substitute W in the rectangle area formula with our new variable to solve for the length.



Solve for length:



Using the length, solve for Width:


Now, plug the length and width into the formula for the perimeter of a rectangle to solve:




The perimeter of the rectangle is 40.
Begin by setting up a ratio of width to length for the rectangle. We know that the width is one-fourth the length, therefore

Now, we can substitute W in the rectangle area formula with our new variable to solve for the length.
Solve for length:
Using the length, solve for Width:
Now, plug the length and width into the formula for the perimeter of a rectangle to solve:
The perimeter of the rectangle is 40.
Compare your answer with the correct one above