How to find the slope of a line - GRE Quantitative Reasoning
Card 0 of 17
What is the slope of line 3 = 8y - 4x?
What is the slope of line 3 = 8y - 4x?
Solve equation for y. y=mx+b, where m is the slope
Solve equation for y. y=mx+b, where m is the slope
Compare your answer with the correct one above
What is the slope of the given linear equation?
2x + 4y = -7
What is the slope of the given linear equation?
2x + 4y = -7
We can convert the given equation into slope-intercept form, y=mx+b, where m is the slope. We get y = (-1/2)x + (-7/2)
We can convert the given equation into slope-intercept form, y=mx+b, where m is the slope. We get y = (-1/2)x + (-7/2)
Compare your answer with the correct one above
Find the slope of the line 6X – 2Y = 14
Find the slope of the line 6X – 2Y = 14
Put the equation in slope-intercept form:
y = mx + b
-2y = -6x +14
y = 3x – 7
The slope of the line is represented by M; therefore the slope of the line is 3.
Put the equation in slope-intercept form:
y = mx + b
-2y = -6x +14
y = 3x – 7
The slope of the line is represented by M; therefore the slope of the line is 3.
Compare your answer with the correct one above
Refer to the following graph:

What is the slope of the line shown?
Refer to the following graph:
What is the slope of the line shown?
One can use either the slope formula m = (y2 – y1)/(x2 – x1) or the standard line equation, y = mx + b to solve for the slope, m. By calculation or observation, one can determine that the slope is –3.
One can use either the slope formula m = (y2 – y1)/(x2 – x1) or the standard line equation, y = mx + b to solve for the slope, m. By calculation or observation, one can determine that the slope is –3.
Compare your answer with the correct one above
What is the slope of the line:

What is the slope of the line:
First put the question in slope intercept form (y = mx + b):
–(1/6)y = –(14/3)x – 7 =>
y = 6(14/3)x – 7
y = 28x – 7.
The slope is 28.
First put the question in slope intercept form (y = mx + b):
–(1/6)y = –(14/3)x – 7 =>
y = 6(14/3)x – 7
y = 28x – 7.
The slope is 28.
Compare your answer with the correct one above
If 2x – 4y = 10, what is the slope of the line?
If 2x – 4y = 10, what is the slope of the line?
First put the equation into slope-intercept form, solving for y: 2x – 4y = 10 → –4y = –2x + 10 → y = 1/2*x – 5/2. So the slope is 1/2.
First put the equation into slope-intercept form, solving for y: 2x – 4y = 10 → –4y = –2x + 10 → y = 1/2*x – 5/2. So the slope is 1/2.
Compare your answer with the correct one above
What is the slope of the equation 4_x_ + 3_y_ = 7?
What is the slope of the equation 4_x_ + 3_y_ = 7?
We should put this equation in the form of y = mx + b, where m is the slope.
We start with 4_x_ + 3_y_ = 7.
Isolate the y term: 3_y_ = 7 – 4_x_
Divide by 3: y = 7/3 – 4/3 * x
Rearrange terms: y = –4/3 * x + 7/3, so the slope is –4/3.
We should put this equation in the form of y = mx + b, where m is the slope.
We start with 4_x_ + 3_y_ = 7.
Isolate the y term: 3_y_ = 7 – 4_x_
Divide by 3: y = 7/3 – 4/3 * x
Rearrange terms: y = –4/3 * x + 7/3, so the slope is –4/3.
Compare your answer with the correct one above
What is the slope of the line with equation 4_x_ – 16_y_ = 24?
What is the slope of the line with equation 4_x_ – 16_y_ = 24?
The equation of a line is:
y = mx + b, where m is the slope
4_x_ – 16_y_ = 24
–16_y_ = –4_x_ + 24
y = (–4_x_)/(–16) + 24/(–16)
y = (1/4)x – 1.5
Slope = 1/4
The equation of a line is:
y = mx + b, where m is the slope
4_x_ – 16_y_ = 24
–16_y_ = –4_x_ + 24
y = (–4_x_)/(–16) + 24/(–16)
y = (1/4)x – 1.5
Slope = 1/4
Compare your answer with the correct one above
What is the slope of a line which passes through coordinates  and
and  ?
?
What is the slope of a line which passes through coordinates 

Slope is found by dividing the difference in the  -coordinates by the difference in the
-coordinates by the difference in the  -coordinates.
-coordinates.

Slope is found by dividing the difference in the 

Compare your answer with the correct one above
What is the slope of a line that passes though the coordinates  and
and  ?
?
What is the slope of a line that passes though the coordinates 

The slope is equal to the difference between the y-coordinates divided by the difference between the x-coordinates.

Use the give points in this formula to calculate the slope.

The slope is equal to the difference between the y-coordinates divided by the difference between the x-coordinates.
Use the give points in this formula to calculate the slope.
Compare your answer with the correct one above
What is the slope of the line represented by the equation  ?
?
What is the slope of the line represented by the equation 
To rearrange the equation into a  format, you want to isolate the
format, you want to isolate the  so that it is the sole variable, without a coefficient, on one side of the equation.
so that it is the sole variable, without a coefficient, on one side of the equation.
First, add  to both sides to get
to both sides to get  .
.
Then, divide both sides by 6 to get  .
.
If you divide each part of the numerator by 6, you get  . This is in a
. This is in a  form, and the
form, and the  is equal to
is equal to  , which is reduced down to
, which is reduced down to  for the correct answer.
for the correct answer.
To rearrange the equation into a 

First, add 

Then, divide both sides by 6 to get 
If you divide each part of the numerator by 6, you get 




Compare your answer with the correct one above
What is the slope of the line  ?
?
What is the slope of the line 
To find the slope, put the equation in slope-intercept form  . In this case we have
. In this case we have  , which indicates that the slope is
, which indicates that the slope is  .
.
To find the slope, put the equation in slope-intercept form 


Compare your answer with the correct one above
What is the slope of a line running through points  and
and  ?
?
What is the slope of a line running through points 

The slope is equal to the difference between the y-coordinates divided by the difference between the x-coordinates.

Use the give points in this formula to calculate the slope.
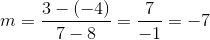
The slope is equal to the difference between the y-coordinates divided by the difference between the x-coordinates.
Use the give points in this formula to calculate the slope.
Compare your answer with the correct one above
What is the slope of the equation  ?
?
What is the slope of the equation 
To find the slope of a line, you should convert an equation to the slope-intercept form. In this case, the equation would be  , which means the slope is
, which means the slope is  .
.
To find the slope of a line, you should convert an equation to the slope-intercept form. In this case, the equation would be 

Compare your answer with the correct one above
What is the slope of a line defined by the equation:

What is the slope of a line defined by the equation:
A question like this is actually rather easy. All you need to do is rewrite the equation in slope intercept form, that is:

Therefore, begin to simplify:

Becomes...

Then...

Finally, divide both sides by  :
:

The coefficient for the  term is your slope:
term is your slope: 
A question like this is actually rather easy. All you need to do is rewrite the equation in slope intercept form, that is:
Therefore, begin to simplify:
Becomes...
Then...
Finally, divide both sides by 
The coefficient for the 
Compare your answer with the correct one above
What is the slope  of a line passing through the point
of a line passing through the point  , if it is defined by:
, if it is defined by:
 ?
?
What is the slope 


Since the equation is defined as it is, you know the y-intercept is  . This is the point
. This is the point  . To find the slope of the line, you merely need to use the two points that you have and find the equation:
. To find the slope of the line, you merely need to use the two points that you have and find the equation:

Since the equation is defined as it is, you know the y-intercept is 

Compare your answer with the correct one above

Which of the following could be an equation for the red line pictured above?

Which of the following could be an equation for the red line pictured above?
There are two key facts to register about this drawing. First, the line clearly has a negative slope, given that it runs "downhill" when you look at it from left to right. Secondly, it has a positive y-intercept. Therefore, you know that the coefficient for the  term must be negative, and the numerical coefficient for the y-intercept must be positive. This only occurs in the equation
term must be negative, and the numerical coefficient for the y-intercept must be positive. This only occurs in the equation  . Therefore, this is the only viable option.
. Therefore, this is the only viable option.
There are two key facts to register about this drawing. First, the line clearly has a negative slope, given that it runs "downhill" when you look at it from left to right. Secondly, it has a positive y-intercept. Therefore, you know that the coefficient for the 

Compare your answer with the correct one above
