How to find out when an equation has no solution - GRE Quantitative Reasoning
Card 0 of 14
Column A: 
Column B: 
Column A:
Column B:
Column B is greater for positive numbers.
The columns are equal for 0.
Column A is greater for negative numbers.
Because our answer changes depending on the value inserted, we cannot determine the relationship.
Column B is greater for positive numbers.
The columns are equal for 0.
Column A is greater for negative numbers.
Because our answer changes depending on the value inserted, we cannot determine the relationship.
Compare your answer with the correct one above
Find the solution to the following equation if x = 3:
y = (4x2 - 2)/(9 - x2)
Find the solution to the following equation if x = 3:
y = (4x2 - 2)/(9 - x2)
Substituting 3 in for x, you will get 0 in the denominator of the fraction. It is not possible to have 0 be the denominator for a fraction so there is no possible solution to this equation.
Substituting 3 in for x, you will get 0 in the denominator of the fraction. It is not possible to have 0 be the denominator for a fraction so there is no possible solution to this equation.
Compare your answer with the correct one above
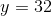
Quantity A: 
Quantity B: 
Quantity A:
Quantity B:
We are given that y = 32. Plug this value of y into the second equation.
32 = x2 – 4
36 = x2
x = +/– 6.
Next find a value for Quantity A:
y/7 = 32/7
This number is less than +6, but more than –6. Thus, the relationship cannot be determined from the information given.
We are given that y = 32. Plug this value of y into the second equation.
32 = x2 – 4
36 = x2
x = +/– 6.
Next find a value for Quantity A:
y/7 = 32/7
This number is less than +6, but more than –6. Thus, the relationship cannot be determined from the information given.
Compare your answer with the correct one above
I. x = 0
II. x = –1
III. x = 1
I. x = 0
II. x = –1
III. x = 1
Compare your answer with the correct one above
Compare your answer with the correct one above
A fraction is considered undefined when the denominator equals 0. Set the denominator equal to zero and solve for the variable.
A fraction is considered undefined when the denominator equals 0. Set the denominator equal to zero and solve for the variable.
Compare your answer with the correct one above
Solve:
Solve:
First, distribute, making sure to watch for negatives.
Combine like terms.
Subtract 7x from both sides.
Add 18 on both sides and be careful adding integers.
First, distribute, making sure to watch for negatives.
Combine like terms.
Subtract 7x from both sides.
Add 18 on both sides and be careful adding integers.
Compare your answer with the correct one above
Solve:
Solve:
First, distribute the 
to the terms inside the parentheses.
Add 6x to both sides.
This is false for any value of 
. Thus, there is no solution.
First, distribute the
Add 6x to both sides.
This is false for any value of
Compare your answer with the correct one above
Solve 
.
Solve
By definition, the absolute value of an expression can never be less than 0. Therefore, there are no solutions to the above expression.
By definition, the absolute value of an expression can never be less than 0. Therefore, there are no solutions to the above expression.
Compare your answer with the correct one above
Quantity A: 
Quantity B: 11
Quantity A:
Quantity B: 11
Expand 
out into 
.
Since 
, it can be seen that 
so Quantity B is greater.
Expand
Since
Compare your answer with the correct one above
Quantity A: 
Quantity B: 
Quantity A:
Quantity B:
Rather than manually finding common denominators and adding the fractions together, realize that
Since
Quantity A must be greater, and this can be seen without actually calculating its value.
Rather than manually finding common denominators and adding the fractions together, realize that
Since
Quantity A must be greater, and this can be seen without actually calculating its value.
Compare your answer with the correct one above
Approximately, what was the percent growth of Beetleton's GDP from 2009 to 2010?
Approximately, what was the percent growth of Beetleton's GDP from 2009 to 2010?
Percent growth is given as:
For Beetleton, this can be expressed as (in terms of billions of US dollars):
Percent growth is given as:
For Beetleton, this can be expressed as (in terms of billions of US dollars):
Compare your answer with the correct one above
The sum of two integers is 
. The larger integer is 
greater than the smaller integer. What is the positive difference between the two?
The sum of two integers is
Let us write down what we are told in mathematical terms, designating the smaller integer as 
and the larger integer as 
.
The sum of the two integers is 
:
And the larger integer is 
% greater than the smaller integer:
Writing the first equation in terms of 
gives:
Which allows us to find 
:
Thus, the positive difference between the two is found as
Let us write down what we are told in mathematical terms, designating the smaller integer as
The sum of the two integers is
And the larger integer is
Writing the first equation in terms of
Which allows us to find
Thus, the positive difference between the two is found as
Compare your answer with the correct one above
Quantity A: 
Quantity B: 
Quantity A:
Quantity B:
To solve this problem, expand each function described by Quantities A and B:
Quantity A: 
Quantity B: 
Now note that Quantities A and B only differ in that Quantity A is greater by 
.
Since we are told that 
is greater than 
and thus always positive, Quantity A must be greater than Quantity B for all possible values of 
.
To solve this problem, expand each function described by Quantities A and B:
Quantity A:
Quantity B:
Now note that Quantities A and B only differ in that Quantity A is greater by
Since we are told that
Compare your answer with the correct one above