Solid Geometry - GRE Quantitative Reasoning
Card 0 of 20
The surface area of a cube is 486 units. What is the distance of its diagonal (e.g. from its front-left-bottom corner to its rear-right-top corner)?
The surface area of a cube is 486 units. What is the distance of its diagonal (e.g. from its front-left-bottom corner to its rear-right-top corner)?
First, we must ascertain the length of each side. Based on our initial data, we know that the 6 faces of the cube will have a surface area of 6x2. This yields the equation:
6x2 = 486, which simplifies to: x2 = 81; x = 9.
Therefore, each side has a length of 9. Imagine the cube is centered on the origin. This means its "front-left-bottom corner" will be at (–4.5, –4.5, 4.5) and its "rear-right-top corner" will be at (4.5, 4.5, –4.5). To find the distance between these, we use the three-dimensional distance formula:
d = √((x1 – x2)2 + (y1 – y2)2 + (z1 – z2)2)
For our data, this will be:
√( (–4.5 – 4.5)2 + (–4.5 – 4.5)2 + (4.5 + 4.5)2) =
√( (–9)2 + (–9)2 + (9)2) = √(81 + 81 + 81) = √(243) =
√(3 * 81) = √(3) * √(81) = 9√(3)
First, we must ascertain the length of each side. Based on our initial data, we know that the 6 faces of the cube will have a surface area of 6x2. This yields the equation:
6x2 = 486, which simplifies to: x2 = 81; x = 9.
Therefore, each side has a length of 9. Imagine the cube is centered on the origin. This means its "front-left-bottom corner" will be at (–4.5, –4.5, 4.5) and its "rear-right-top corner" will be at (4.5, 4.5, –4.5). To find the distance between these, we use the three-dimensional distance formula:
d = √((x1 – x2)2 + (y1 – y2)2 + (z1 – z2)2)
For our data, this will be:
√( (–4.5 – 4.5)2 + (–4.5 – 4.5)2 + (4.5 + 4.5)2) =
√( (–9)2 + (–9)2 + (9)2) = √(81 + 81 + 81) = √(243) =
√(3 * 81) = √(3) * √(81) = 9√(3)
Compare your answer with the correct one above
You have a rectangular box with dimensions 6 inches by 6 inches by 8 inches. What is the length of the shortest distance between two non-adjacent corners of the box?
You have a rectangular box with dimensions 6 inches by 6 inches by 8 inches. What is the length of the shortest distance between two non-adjacent corners of the box?
The shortest length between any two non-adjacent corners will be the diagonal of the smallest face of the rectangular box. The smallest face of the rectangular box is a six-inch by six-inch square. The diagonal of a six-inch square is  .
.
The shortest length between any two non-adjacent corners will be the diagonal of the smallest face of the rectangular box. The smallest face of the rectangular box is a six-inch by six-inch square. The diagonal of a six-inch square is 
Compare your answer with the correct one above
What is the length of the diagonal of a cube with side lengths of 
 each?
each?
What is the length of the diagonal of a cube with side lengths of 

The diagonal length of a cube is found by a form of the distance formula that is akin to the Pythagorean Theorem, though with an additional dimension added to it. It is:
 , or
, or  , or
, or 
Now, if the the value of  is
is  , we get simply
, we get simply 
The diagonal length of a cube is found by a form of the distance formula that is akin to the Pythagorean Theorem, though with an additional dimension added to it. It is:


Now, if the the value of 

Compare your answer with the correct one above
What is the length of the diagonal of a cube that has a surface area of 
 ?
?
What is the length of the diagonal of a cube that has a surface area of 

To begin, the best thing to do is to find the length of a side of the cube. This is done using the formula for the surface area of a cube. Recall that a cube is made up of  squares. Therefore, its surface area is:
squares. Therefore, its surface area is:
 , where
, where  is the length of a side.
is the length of a side.
Therefore, for our data, we have:

Solving for  , we get:
, we get:

This means that 
Now, the diagonal length of a cube is found by a form of the distance formula that is akin to the Pythagorean Theorem, though with an additional dimension added to it. It is:
 , or
, or  , or
, or 
Now, if the the value of  is
is  , we get simply
, we get simply 
To begin, the best thing to do is to find the length of a side of the cube. This is done using the formula for the surface area of a cube. Recall that a cube is made up of 


Therefore, for our data, we have:
Solving for 
This means that
Now, the diagonal length of a cube is found by a form of the distance formula that is akin to the Pythagorean Theorem, though with an additional dimension added to it. It is:


Now, if the the value of 

Compare your answer with the correct one above
A cube with a surface area of 216 square units has a side length that is equal to the diameter of a certain sphere. What is the surface area of the sphere?
A cube with a surface area of 216 square units has a side length that is equal to the diameter of a certain sphere. What is the surface area of the sphere?
Begin by solving for the length of one side of the cube. Use the formula for surface area to do this:

s= length of one side of the cube



The length of the side of the cube is equal to the diameter of the sphere. Therefore, the radius of the sphere is 3. Now use the formula for the surface area of a sphere:






The surface area of the sphere is  .
.
Begin by solving for the length of one side of the cube. Use the formula for surface area to do this:
s= length of one side of the cube
The length of the side of the cube is equal to the diameter of the sphere. Therefore, the radius of the sphere is 3. Now use the formula for the surface area of a sphere:
The surface area of the sphere is 
Compare your answer with the correct one above
The surface area of a sphere is  . What is its diameter?
. What is its diameter?
The surface area of a sphere is 
The surface area of a sphere is defined by the equation:

For our data, this means:

Solving for  , we get:
, we get:
 or
or 
The diameter of the sphere is  .
.
The surface area of a sphere is defined by the equation:
For our data, this means:
Solving for 

The diameter of the sphere is 
Compare your answer with the correct one above
The volume of one sphere is  . What is the diameter of a sphere of half that volume?
. What is the diameter of a sphere of half that volume?
The volume of one sphere is 
Do not assume that the diameter will be half of the diameter of a sphere with volume of  . Instead, begin with the sphere with a volume of
. Instead, begin with the sphere with a volume of  . Such a simple action will prevent a vexing error!
. Such a simple action will prevent a vexing error!
Thus, we know from our equation for the volume of a sphere that:

Solving for  , we get:
, we get:

If you take the cube-root of both sides, you have:
![r = \sqrt[3]{162x^3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/385691/gif.latex)
First, you can factor out an  :
:
![r = x\sqrt[3]{162}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/385693/gif.latex)
Next, factor the  :
:
![r = x\sqrt[3]{2*3^4}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/385695/gif.latex)
Which simplifies to:
![r = 3x\sqrt[3]{6}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/385696/gif.latex)
Thus, the diameter is double that or:
![6x\sqrt[3]{6}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/385697/gif.latex)
Do not assume that the diameter will be half of the diameter of a sphere with volume of 

Thus, we know from our equation for the volume of a sphere that:
Solving for 
If you take the cube-root of both sides, you have:
First, you can factor out an 
Next, factor the 
Which simplifies to:
Thus, the diameter is double that or:
Compare your answer with the correct one above
Quantity A: The length of a side of a cube with a volume of 
 .
.
Quantity B: The length of a side of a cube with surface area of 
 .
.
Which of the following is true?
Quantity A: The length of a side of a cube with a volume of 

Quantity B: The length of a side of a cube with surface area of 

Which of the following is true?
Recall that the equation for the volume of a cube is:

Since the sides of a cube are merely squares, the surface area equation is just  times the area of one of those squares:
times the area of one of those squares:

So, for our two quantities:
Quantity A

Use your calculator to estimate this value (since you will not have a square root key). This is  .
.
Quantity B

First divide by  :
:

Therefore, 
Therefore, the two quantities are equal.
Recall that the equation for the volume of a cube is:
Since the sides of a cube are merely squares, the surface area equation is just 
So, for our two quantities:
Quantity A
Use your calculator to estimate this value (since you will not have a square root key). This is 
Quantity B
First divide by 
Therefore,
Therefore, the two quantities are equal.
Compare your answer with the correct one above
What is the length of an edge of a cube with a surface area of  ?
?
What is the length of an edge of a cube with a surface area of 
The surface area of a cube is made up of  squares. Therefore, the equation is merely
squares. Therefore, the equation is merely  times the area of one of those squares. Since the sides of a square are equal, this is:
times the area of one of those squares. Since the sides of a square are equal, this is:
 , where
, where  is the length of one side of the square.
is the length of one side of the square.
For our data, we know:

This means that:

Now, while you will not have a calculator with a square root key, you do know that  . (You can always use your calculator to test values like this.) Therefore, we know that
. (You can always use your calculator to test values like this.) Therefore, we know that  . This is the length of one side
. This is the length of one side
The surface area of a cube is made up of 



For our data, we know:
This means that:
Now, while you will not have a calculator with a square root key, you do know that 

Compare your answer with the correct one above
If a cube has a total surface area of  square inches, what is the length of one edge?
square inches, what is the length of one edge?
If a cube has a total surface area of 
There are 6 sides to a cube. If the total surface area is 54 square inches, then each face must have an area of 9 square inches.



Every face of a cube is a square, so if the area is 9 square inches, each edge must be 3 inches.
There are 6 sides to a cube. If the total surface area is 54 square inches, then each face must have an area of 9 square inches.
Every face of a cube is a square, so if the area is 9 square inches, each edge must be 3 inches.
Compare your answer with the correct one above
The surface area of a rectangular prism is  , and the lengths of two sides are
, and the lengths of two sides are 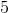 and
and 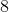 . What is the volume of the prism?
. What is the volume of the prism?
The surface area of a rectangular prism is 
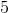
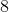
The surface area of a rectangular prism with sides  ,
,  , and
, and 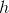 is given as:
is given as:
 .
.
Two sides are known; it does not matter how they are designated, but for this problem let  and
and  , with
, with  as the unknown side. This yields equality:
as the unknown side. This yields equality:
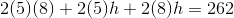

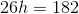

Now that the three dimensions are known, it's possible to calculate the volume:

The surface area of a rectangular prism with sides 

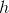

Two sides are known; it does not matter how they are designated, but for this problem let 


Now that the three dimensions are known, it's possible to calculate the volume:
Compare your answer with the correct one above
What is the radius of a sphere with volume  cubed units?
cubed units?
What is the radius of a sphere with volume 
The volume of a sphere is represented by the equation  . Set this equation equal to the volume given and solve for r:
. Set this equation equal to the volume given and solve for r:





Therefore, the radius of the sphere is 3.
The volume of a sphere is represented by the equation 
Therefore, the radius of the sphere is 3.
Compare your answer with the correct one above
If a sphere has a volume of  cubic inches, what is the approximate radius of the sphere?
cubic inches, what is the approximate radius of the sphere?
If a sphere has a volume of 
The formula for the volume of a sphere is
 where
where  is the radius of the sphere.
is the radius of the sphere.
Therefore,
![r=\sqrt[3]{\frac{3v}{(4\pi)}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/345687/gif.latex)
![r=\sqrt[3]{\frac{3(268.08)}{(4\pi)}}=\sqrt[3]{63.999}=3.999](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/345688/gif.latex) , giving us
, giving us  .
.
The formula for the volume of a sphere is


Therefore,
![r=\sqrt[3]{\frac{3(268.08)}{(4\pi)}}=\sqrt[3]{63.999}=3.999](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/345688/gif.latex)

Compare your answer with the correct one above
A rectangular prism has the dimensions  . What is the volume of the largest possible sphere that could fit within this solid?
. What is the volume of the largest possible sphere that could fit within this solid?
A rectangular prism has the dimensions 
For a sphere to fit into the rectangular prism, its dimensions are constrained by the prism's smallest side, which forms its diameter. Therefore, the largest sphere will have a diameter of  , and a radius of
, and a radius of  .
.
The volume of a sphere is given as:

And thus the volume of the largest possible sphere to fit into this prism is

For a sphere to fit into the rectangular prism, its dimensions are constrained by the prism's smallest side, which forms its diameter. Therefore, the largest sphere will have a diameter of 

The volume of a sphere is given as:
And thus the volume of the largest possible sphere to fit into this prism is
Compare your answer with the correct one above
A rectangular box is 6 feet wide, 3 feet long, and 2 feet high. What is the surface area of this box?
A rectangular box is 6 feet wide, 3 feet long, and 2 feet high. What is the surface area of this box?
The surface area formula we need to solve this is 2_ab_ + 2_bc_ + 2_ac_. So if we let a = 6, b = 3, and c = 2, then surface area:
= 2(6)(3) + 2(3)(2) +2(6)(2)
= 72 sq ft.
The surface area formula we need to solve this is 2_ab_ + 2_bc_ + 2_ac_. So if we let a = 6, b = 3, and c = 2, then surface area:
= 2(6)(3) + 2(3)(2) +2(6)(2)
= 72 sq ft.
Compare your answer with the correct one above
What is the surface area of a rectangular box that is 3 feet high, 6 feet long, and 4 feet wide?
What is the surface area of a rectangular box that is 3 feet high, 6 feet long, and 4 feet wide?
Surface area of a rectangular solid
= 2_lw_ + 2_lh_ + 2_wh_
= 2(6)(4) + 2(6)(3) + 2(4)(3)
= 108
Surface area of a rectangular solid
= 2_lw_ + 2_lh_ + 2_wh_
= 2(6)(4) + 2(6)(3) + 2(4)(3)
= 108
Compare your answer with the correct one above
A large cube is made by fitting 8 smaller, identical cubes together. If the volume of each of the smaller cubes is 27, what is the surface area of the large cube?
A large cube is made by fitting 8 smaller, identical cubes together. If the volume of each of the smaller cubes is 27, what is the surface area of the large cube?
Since the volume of the smaller cubes with edges,  , is 27, we have:
, is 27, we have:
 .
.
The large cube has edges  .
.
So the surface area of the large cube is:
 .
.
Since the volume of the smaller cubes with edges, 

The large cube has edges 
So the surface area of the large cube is:

Compare your answer with the correct one above
Quantity A:
The surface area of a cube with a volume of  .
.
Quantity B:
The volume of a cube with a surface area of  .
.
Quantity A:
The surface area of a cube with a volume of 
Quantity B:
The volume of a cube with a surface area of 
The relationship can be determined, because it is possible to find the surface area of a cube from the volume and vice versa.
Quantity A:
To find the surface area of the cube, you must find the side length. To find the side length from the volume, you must find the cube root.
Find the cube root of the volume.
![\sqrt[3]{729} = 9](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/253445/gif.latex)
Insert into surface area equation.




Quantity B:
To find the volume of a cube, you must find the side length. To find the side length from the surface area, you must divide by 6, then find the square root of the result. Then, cube that result.

Divide by 6.

Square root.

Now, to find the volume.



Quantity B is greater.
The relationship can be determined, because it is possible to find the surface area of a cube from the volume and vice versa.
Quantity A:
To find the surface area of the cube, you must find the side length. To find the side length from the volume, you must find the cube root.
Find the cube root of the volume.
Insert into surface area equation.
Quantity B:
To find the volume of a cube, you must find the side length. To find the side length from the surface area, you must divide by 6, then find the square root of the result. Then, cube that result.
Divide by 6.
Square root.
Now, to find the volume.
Quantity B is greater.
Compare your answer with the correct one above
The area of the base of a circular right cylinder is quadrupled. By what percentage is the outer face increased by this change?
The area of the base of a circular right cylinder is quadrupled. By what percentage is the outer face increased by this change?
The base of the original cylinder would have been πr2, and the outer face would have been 2πrh, where h is the height of the cylinder.
Let's represent the original area with A, the original radius with r, and the new radius with R: therefore, we know πR2 = 4A, or πR2 = 4πr2. Solving for R, we get R = 2r; therefore, the new outer face of the cylinder will have an area of 2πRh or 2π2rh or 4πrh, which is double the original face area; thus the percentage of increase is 100%. (Don't be tricked into thinking it is 200%. That is not the percentage of increase.)
The base of the original cylinder would have been πr2, and the outer face would have been 2πrh, where h is the height of the cylinder.
Let's represent the original area with A, the original radius with r, and the new radius with R: therefore, we know πR2 = 4A, or πR2 = 4πr2. Solving for R, we get R = 2r; therefore, the new outer face of the cylinder will have an area of 2πRh or 2π2rh or 4πrh, which is double the original face area; thus the percentage of increase is 100%. (Don't be tricked into thinking it is 200%. That is not the percentage of increase.)
Compare your answer with the correct one above
A cylinder has a radius of 4 and a height of 8. What is its surface area?
A cylinder has a radius of 4 and a height of 8. What is its surface area?
This problem is simple if we remember the surface area formula!

This problem is simple if we remember the surface area formula!
Compare your answer with the correct one above