Exponents and Rational Numbers - GRE Quantitative Reasoning
Card 0 of 16
Quantity A: 
Quantity B: 
Quantity A:
Quantity B:
(–1) 137= –1
–1 < 0
(–1) odd # always equals –1.
(–1) even # always equals +1.
(–1) 137= –1
–1 < 0
(–1) odd # always equals –1.
(–1) even # always equals +1.
Compare your answer with the correct one above
Quantitative Comparison: Compare Quantity A and Quantity B, using additional information centered above the two quantities if such information is given.
Quantity A Quantity B
43 34
Quantitative Comparison: Compare Quantity A and Quantity B, using additional information centered above the two quantities if such information is given.
Quantity A Quantity B
43 34
In order to determine the relationship between the quantities, solve each quantity.
43 is 4 * 4 * 4 = 64
34 is 3 * 3 * 3 * 3 = 81
Therefore, Quantity B is greater.
In order to determine the relationship between the quantities, solve each quantity.
43 is 4 * 4 * 4 = 64
34 is 3 * 3 * 3 * 3 = 81
Therefore, Quantity B is greater.
Compare your answer with the correct one above
Anything raised to negative power means  over the base raised to the postive exponent.
over the base raised to the postive exponent.

Anything raised to negative power means 
Compare your answer with the correct one above
Simplify

Simplify
Whenever you see lots of multiplication (e.g. exponents, which are notation for repetitive multiplication) separated by addition or subtraction, a common way to transform the expression is to factor out common terms on either side of the + or - sign. That allows you to create more multiplication, which is helpful in reducing fractions or in reducing the addition/subtraction to numbers you can quickly calculate by hand as you'll see here.
So let's factor a  .
.
We have  .
.
And you'll see that the addition inside parentheses becomes quite manageable, leading to the final answer of  .
.
Whenever you see lots of multiplication (e.g. exponents, which are notation for repetitive multiplication) separated by addition or subtraction, a common way to transform the expression is to factor out common terms on either side of the + or - sign. That allows you to create more multiplication, which is helpful in reducing fractions or in reducing the addition/subtraction to numbers you can quickly calculate by hand as you'll see here.
So let's factor a 
We have 
And you'll see that the addition inside parentheses becomes quite manageable, leading to the final answer of 
Compare your answer with the correct one above
Which of the following is not the same as the others?
Which of the following is not the same as the others?
Let's all convert the bases to  .
.
![4^{12}=[2^2]^{12}=2^{24}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/340115/gif.latex)

![16^8=[2^4]^8=2^{32}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/340117/gif.latex)
 This one may be intimidating but
This one may be intimidating but 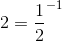 .
.
Therefore,
![\left(\left[\frac{1}{2}\right]^{-24}\right)^{-1}=2^{24}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/342256/gif.latex)

 is not like the answers so this is the correct answer.
is not like the answers so this is the correct answer.
Let's all convert the bases to 

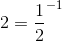
Therefore,

Compare your answer with the correct one above
find x
8x=2x+6
find x
8x=2x+6
8 = 23
(23)x = 23x
23x = 2x+6 <- when the bases are the same, you can set the exponents equal to each other and solve for x
3x=x+6
2x=6
x=3
8 = 23
(23)x = 23x
23x = 2x+6 <- when the bases are the same, you can set the exponents equal to each other and solve for x
3x=x+6
2x=6
x=3
Compare your answer with the correct one above
Compare  and
and  .
.
Compare 

First rewrite the two expressions so that they have the same base, and then compare their exponents.


Combine exponents by multiplying: 
This is the same as the first given expression, so the two expressions are equal.
First rewrite the two expressions so that they have the same base, and then compare their exponents.
Combine exponents by multiplying:
This is the same as the first given expression, so the two expressions are equal.
Compare your answer with the correct one above
Solve for  .
.

Solve for 
 can be written as
can be written as 
Since there is a common base of  , we can say
, we can say
 or
or  .
.

Since there is a common base of 


Compare your answer with the correct one above
Solve for  .
.

Solve for 
The basees don't match.
However:
 thus we can rewrite the expression as
thus we can rewrite the expression as  .
.
Anything raised to negative power means  over the base raised to the postive exponent.
over the base raised to the postive exponent.
So, 
 .
.  .
.
The basees don't match.
However:


Anything raised to negative power means 
So, 

Compare your answer with the correct one above
Solve for  .
.

Solve for 
The bases don't match.
However:
 and we recognize that
and we recognize that  .
.
Anything raised to negative power means  over the base raised to the postive exponent.
over the base raised to the postive exponent.
 .
.

The bases don't match.
However:


Anything raised to negative power means 

Compare your answer with the correct one above
Solve for 

Solve for
Recall that  .
.
With same base, we can write this equation:
 .
.
By subtracting  on both sides,
on both sides,  .
.
Recall that 
With same base, we can write this equation:

By subtracting 

Compare your answer with the correct one above
Solve for  .
.

Solve for 
Since  we can rewrite the expression.
we can rewrite the expression.
With same base, let's set up an equation of  .
.
By subtracting  on both sides, we get
on both sides, we get  .
.
Take the square root of both sides we get BOTH  and
and  .
.
Since 
With same base, let's set up an equation of 
By subtracting 

Take the square root of both sides we get BOTH 

Compare your answer with the correct one above
Solve for  .
.

Solve for 
They don't have the same base, however:  .
.
Then  . You would multiply the
. You would multiply the  and the
and the  instead of adding.
instead of adding.
 .
.

They don't have the same base, however: 
Then 



Compare your answer with the correct one above
Solve for  .
.

Solve for 
There are two ways to go about this.
Method 
They don't have the same bases however:  . Then
. Then 
You would multiply the  and the
and the  instead of adding. We have
instead of adding. We have 
Divide  on both sides to get
on both sides to get  .
.
Method  :
:
We can change the base from  to
to 

This is the basic property of the product of power exponents.
We have the same base so basically  .
.
There are two ways to go about this.
Method
They don't have the same bases however: 
You would multiply the 

Divide 

Method 
We can change the base from 
This is the basic property of the product of power exponents.
We have the same base so basically 
Compare your answer with the correct one above
Solve for  .
.

Solve for 
Since we can write  .
.
With same base we can set up an equation of 
Divide both sides by  and we get
and we get  .
.
Since we can write 
With same base we can set up an equation of
Divide both sides by 

Compare your answer with the correct one above
Solve for  .
.

Solve for 

We still don't have the same base however: 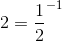
Then,
![1024^x=(2^{10})^x=\left[\left(\frac{1}{2}\right)^{-1}\right]^{10x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/342249/gif.latex) .
.
With same base we can set up an equation of  .
.
Divide both sides by  and we get
and we get  .
.
We still don't have the same base however:
Then,
![1024^x=(2^{10})^x=\left[\left(\frac{1}{2}\right)^{-1}\right]^{10x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/342249/gif.latex)
With same base we can set up an equation of 
Divide both sides by 

Compare your answer with the correct one above
