Algebra - GRE Quantitative Reasoning

Card 0 of 20

Question

If $5^2 \times 5^n = 5^{12}$ , what is the value of ?

Answer

Since the base is 5 for each term, we can say 2 + n =12. Solve the equation for n by subtracting 2 from both sides to get n = 10.

Compare your answer with the correct one above

Question

Simplify: y3x4(yx3 + y2x2 + y15 + x22)

Answer

When you multiply exponents, you add the common bases:

y4 x7 + y5x6 + y18x4 + y3x26

Compare your answer with the correct one above

Question

Indicate whether Quantity A or Quantity B is greater, or if they are equal, or if there is not enough information given to determine the relationship.

$\dpi{100} \small n>0$

Quantity A: $\dpi{100} \small 16^{n+2}$

Quantity B: $\dpi{100} \small 2^{4}\times (8^{n+1})^{2}\div 4^{n}$

Answer

By using exponent rules, we can simplify Quantity B.

$\dpi{100} \small \dpi{100} \small 2^{4}\times (8^{n+1})^{2}\div 4^{n}$

$\dpi{100} \small \dpi{100} \small 2^{4}\times (8^{2n+2})\div 4^{n}$

$\dpi{100} \small \dpi{100} \small 2^{4}\times 2^{3(2n+2)}\div 4^{n}$

$\dpi{100} \small \dpi{100} \small 2^{4}\times 2^{6n+6}\div 4^{n}$

$\dpi{100} \small \dpi{100} \small 2^{6n+10}\div 4^{n}$

$\dpi{100} \small \dpi{100} \small 2^{6n+10}\div 2^{2n}$

$\dpi{100} \small 2^{4n+10}$

Also, we can simplify Quantity A.

$\dpi{100} \small 16^{n+2}$

$\dpi{100} \small =2^{4(n+2)}$

$\dpi{100} \small =2^{4n+8}$

Since n is positive, $\dpi{100} \small 4n+10>4n+8$

Compare your answer with the correct one above

Question

If $\frac{3^{y - 1}}{3^{-2}} = 27^{y}3^{y}$ , what is the value of ?

Answer

Rewrite the term on the left as a product. Remember that negative exponents shift their position in a fraction (denominator to numerator).

$3^{y-1}3^2=27^y3^y$

The term on the right can be rewritten, as 27 is equal to 3 to the third power.

$3^{y-1}3^2=(3^3)^y3^y$

Exponent rules dictate that multiplying terms allows us to add their exponents, while one term raised to another allows us to multiply exponents.

$3^{(y-1)+2}=(3)^{3y}3^y$

$3^{y+1}=3^{3y+y}=3^{4y}$

We now know that the exponents must be equal, and can solve for .

$\frac{1}{3}=y$

Compare your answer with the correct one above

Question

Simplify $x^{^{3}}x^{^{5}} - x^{^{2}} + (y^{^{2}})^{^{2}}$ .

Answer

First, simplify $x^{3}x^{5}$ by adding the exponents to get $x^{8}$ .

Then simplify $(y^{2})^{2}$ by multiplying the exponents to get $y^{4}$ .

This gives us $x^{8} - x^{^{2}} + y^{4}$ . We cannot simplify any further.

Compare your answer with the correct one above

Question

Simplify $x^{3}x^{6} + (x^{3})^{3} + x^{3}x^{2}x^{2}x^{2}$ .

Answer

Start by simplifying each individual term between the plus signs. We can add the exponents in and so each of those terms becomes . Then multiply the exponents in so that term also becomes . Thus, we have simplified the expression to which is $3x^{9}$ .

Compare your answer with the correct one above

Question

If $3^4 \cdot 3^8 = 9^x$ , what is the value of

Answer

To attempt this problem, note that .

Now note that when multiplying numbers, if the base is the same, we may add the exponents:

$3^4 \cdot 3^8 = 3^{4+8}=3^{12}$

This can in turn be written in terms of nine as follows (recall above)

$3^{12}=9^{\frac{12}{2}}=9^6$

Compare your answer with the correct one above

Question

If $(3^2\cdot3^5)^3=3^x$ , what is the value of

Answer

When dealing with exponenents, when multiplying two like bases together, add their exponents:

$3^2\cdot3^5=3^7$

However, when an exponent appears outside of a parenthesis, or if the entire number itself is being raised by a power, multiply:

$(3^7)^3=3^{7\cdot 3}=3^{21}$

$3^{21}=3^{x}$

Compare your answer with the correct one above

Question

Simplify the following rational expression: (9x - 2)/(x2) MINUS (6x - 8)/(x2)

Answer

Since both expressions have a common denominator, x2, we can just recopy the denominator and focus on the numerators. We get (9x - 2) - (6x - 8). We must distribute the negative sign over the 6x - 8 expression which gives us 9x - 2 - 6x + 8 ( -2 minus a -8 gives a +6 since a negative and negative make a positive). The numerator is therefore 3x + 6.

Compare your answer with the correct one above

Question

Simplify the following rational expression:

$\frac{7x-18}{x^{2}}+\frac{6x-14}{x^{2}}$

Answer

Since both fractions in the expression have a common denominator of $x^{2}$ , we can combine like terms into a single numerator over the denominator:

$\frac{7x-18}{x^{2}}+\frac{6x-14}{x^{2}}$

$=\frac{(7x-18)+(6x-14)}{x^{2}}$

$=\frac{13x-32}{x^{2}}$

Compare your answer with the correct one above

Question

Simplify the following rational expression:

$\frac{5x-5}{2x^{2}} + \frac{7x+9}{2x^{2}}$

Answer

Since both rational terms in the expression have the common denominator $2x^{2}$ , combine the numerators and simplify like terms:

$\frac{5x-5}{2x^{2}} + \frac{7x+9}{2x^{2}}$

$=\frac{(5x-5)+(7x+9)}{2x^{2}}$

$=\frac{12x+4}{2x^{2}}$

$=\frac{6x+2}{x^2}$

Compare your answer with the correct one above

Question

Simplify the following expression:

$\frac{10x-9}{x^{3}}+\frac{11x+12}{x^{3}}$

Answer

Since both terms in the expression have the common denominator $x^{3}$ , combine the fractions and simplify the numerators:

$\frac{10x-9}{x^{3}}+\frac{11x+12}{x^{3}}$

$=\frac{(10x-9)+(11x+12)}{x^{3}}$

$=\frac{21x+3}{x^{3}}$

Compare your answer with the correct one above

Question

Add and simplify:

$\frac{3x^2 + 3x + 3}{2y} + \frac{10x^2 + 3x}{2y}$

Answer

When adding rational expressions with common denominators, you simply need to add the like terms in the numerator.

Therefore, $\frac{13x^2 + 6x + 3}{2y}$ is the best answer.

Compare your answer with the correct one above

Question

Simplify the expression.

$\frac{x}{2x+4}+\frac{x}{x+2}$

Answer

To add rational expressions, first find the least common denominator. Because the denominator of the first fraction factors to 2(x+2), it is clear that this is the common denominator. Therefore, multiply the numerator and denominator of the second fraction by 2.

$\frac{x}{2x+4}+\frac{x}{x+2}$

$\frac{x}{2x+4}+\frac{(2)x}{(2)(x+2)}$

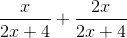
$\frac{x}{2x+4}+\frac{2x}{2x+4}$

$\frac{3x}{2x+4}$

This is the most simplified version of the rational expression.

Compare your answer with the correct one above

Question

Simplify the following:

$\frac{x+3}{x-2}+\frac{x-2}{x+3}$

Answer

To simplify the following, a common denominator must be achieved. In this case, the first term must be multiplied by (x+2) in both the numerator and denominator and likewise with the second term with (x-3).

$\frac{(x+3)(x+3)}{(x-2)(x+3)}+\frac{(x-2)(x-2)}{(x+3)(x-2)}$

$\frac{(x+3)^2+(x-2)^2}{(x+3)(x-2)}$

Compare your answer with the correct one above

Question

Choose the answer which best simplifies the following expression:

$\frac{3p}{2} + \frac{2p}{p^3}$

Answer

To simplify this expression, you have to get both numerators over a common denominator. The best way to go about doing so is to multiply both expressions by the others denominator over itself:

$\frac{3p}{2} \cdot \frac{p^3}{p^3 } + \frac{2p}{p^3} \cdot \frac{2}{2}$

Then you are left with:

$\frac{3p^4}{2p^3} + \frac{4p}{2p^3}$

Which you can simplify into:

$\frac{3p^4+4p}{2p^3}$

From there, you can take out a :

$\frac{p(3p^3 + 4)}{p(2p^2)}$

Which gives you your final answer:

$\frac{3p^3 +4}{2p^2}$

Compare your answer with the correct one above

Question

Choose the answer which best simplifies the following expression:

$\frac{2a + 2}{3} + \frac{3}{a^2}$

Answer

To solve this problem, first multiply both terms of the expression by the denominator of the other over itself:

$\frac{2a + 2}{3} \cdot \frac{a^2}{a^2} + \frac{3}{a^2} \cdot \frac{3}{3}$

$\frac{2a^3 +2a^2}{3a^2} + \frac{9}{3a^2}$

Now that both terms have a common denominator, you can add them together:

$\frac{2a^3 +2a^2 + 9}{3a^2}$

Compare your answer with the correct one above

Question

Choose the answer which best simplifies the following expression:

$\frac{3a^2 + a}{2} + \frac{10}{2a^2-a}$

Answer

To simplify, first multiply both terms by the denominator of the other term over itself:

$\frac{3a^2 + a}{2} \left(\frac{2a^2 - a}{2a^2 - a}\right) + \frac{10}{2a^2-a}\left(\frac{2}{2}\right)$

$\frac{6a^4 + 2a^3 -3a^3 - a^2}{4a^2 -2a} + \frac{20}{4a^2 - 2a}$

Then, you can combine the terms, now that they share a denominator:

$\frac{6a^4 - a^3 -a^2 +20}{4a^2 - 2a}$

Compare your answer with the correct one above

Question

If , then $\frac{(c^3)^2}{c^2c^4}=?$

Answer

Start by simplifying the numerator and denominator separately. In the numerator, (c3)2 is equal to c6. In the denominator, c2 * c4 equals c6 as well. Dividing the numerator by the denominator, c6/c6, gives an answer of 1, because the numerator and the denominator are the equivalent.

Compare your answer with the correct one above

Question

Evaluate:

$\frac{(2x^3y^{-2}a^6z^4)^5}{(4xy^4a^{-3}z^4)^2}$

Answer

Distribute the outside exponents first:

$\frac{2^5x^{15}y^{-10}a^{30}z^{20}}{4^2x^2y^8a^{-6}z^8}$

Divide the coefficient by subtracting the denominator exponents from the corresponding numerator exponents:

$\frac{2x^{13}a^{36}z^{12}}{y^{18}}$

Compare your answer with the correct one above

Tap the card to reveal the answer