Right Triangles - GMAT Quantitative Reasoning
Card 0 of 20

Right triangle  has length
has length  and
and  . How many degrees is angle
. How many degrees is angle  ?
?

Right triangle 



For any right triangle, whose sides are in ratio  , where
, where  is a constant, its angles must be
is a constant, its angles must be  and
and  . Here the triangle has its sides in that ratio with
. Here the triangle has its sides in that ratio with  . Therefore, angle B must be the smallest angle,
. Therefore, angle B must be the smallest angle,  , since it is the angle between the two longest sides. This rule is really useful on the test, and it is advised to memorize it!
, since it is the angle between the two longest sides. This rule is really useful on the test, and it is advised to memorize it!
For any right triangle, whose sides are in ratio 





Compare your answer with the correct one above
Of the two acute angles of a right triangle, one measures fifteen degrees less than twice the other. What is the measure of the smaller of the two angles?
Of the two acute angles of a right triangle, one measures fifteen degrees less than twice the other. What is the measure of the smaller of the two angles?
Let one of the angles measure  ; then the other angle measures
; then the other angle measures  . The sum of the measures of the acute angles of a triangle is
. The sum of the measures of the acute angles of a triangle is  , so we can set up and solve this equation:
, so we can set up and solve this equation:





The acute angles measure  ; since we want the smaller of the two,
; since we want the smaller of the two,  is the correct choice.
is the correct choice.
Let one of the angles measure 


The acute angles measure 

Compare your answer with the correct one above
For a certain right triangle, the angle between the base and the hypotenuse is 36 degrees. What is the measure of the only remaining unknown angle?
For a certain right triangle, the angle between the base and the hypotenuse is 36 degrees. What is the measure of the only remaining unknown angle?
By definition, one of the angles of a right triangle must be 90 degrees. We are given the measure of another angle in the problem, so we now know the measure of two angles in the triangle. Because the sum of the angles of any triangle is 180 degrees, we can then solve for the measure of the only remaining unknown angle:



By definition, one of the angles of a right triangle must be 90 degrees. We are given the measure of another angle in the problem, so we now know the measure of two angles in the triangle. Because the sum of the angles of any triangle is 180 degrees, we can then solve for the measure of the only remaining unknown angle:
Compare your answer with the correct one above

Triangle  is a right triangle, with
is a right triangle, with  . What is the size of angle
. What is the size of angle  ?
?

Triangle 


Triangle ABC is an isosceles right triangle. Therefore, its angles at the basis BC will always be  .
.
This stems from the fact that the sums of the angles of a triangle are  and in our case with ABC a right and isosceles triangle,
and in our case with ABC a right and isosceles triangle,  , therefore for the two remaining angles are equal.
, therefore for the two remaining angles are equal.
There are 90 degrees left, therefore to find the measure of each angle we do the following,
 .
.
Triangle ABC is an isosceles right triangle. Therefore, its angles at the basis BC will always be 
This stems from the fact that the sums of the angles of a triangle are 

There are 90 degrees left, therefore to find the measure of each angle we do the following,

Compare your answer with the correct one above

 is a right triangle, with sides
is a right triangle, with sides  . What is the size of angle
. What is the size of angle  ?
?




Here, we can tell the size of the angles by recognizing the length of the sides indicative of a right triangle with angles  .
.
Indeed, the length of the sides are  and
and  . Any triangle with sides
. Any triangle with sides  , where
, where  is a constant, will have angles
is a constant, will have angles  .
.
In our case  . Therefore, angle
. Therefore, angle  will be the smallest of the three possible angles, since it is between the two longest sides ( the hypotenuse and AB, which is longer than AC). Therefore the larger angle
will be the smallest of the three possible angles, since it is between the two longest sides ( the hypotenuse and AB, which is longer than AC). Therefore the larger angle  will be
will be  thus arriving at our final answer.
thus arriving at our final answer.
Here, we can tell the size of the angles by recognizing the length of the sides indicative of a right triangle with angles 
Indeed, the length of the sides are 




In our case 



Compare your answer with the correct one above
The measures of the acute angles of a right triangle are  and
and  . Also,
. Also,
 .
.
Evaluate  .
.
The measures of the acute angles of a right triangle are 


Evaluate 
The measures of the acute angles of a right triangle have sum  , so
, so

Along with  , a system of linear equations can be formed and solved as follows:
, a system of linear equations can be formed and solved as follows:





The measures of the acute angles of a right triangle have sum 
Along with 
Compare your answer with the correct one above
Given a right triangle  with right angle
with right angle  , what is the measure of
, what is the measure of  ?
?
Statement 1: 
Statement 2: 
Given a right triangle 


Statement 1:
Statement 2:
Let  be the measure of
be the measure of  . The sum of the measures of the acute angles of a right triangle,
. The sum of the measures of the acute angles of a right triangle,  and
and  , is
, is  , so
, so




Assume Statement 1 alone. This can be rewritten:







Assume Statement 2 alone. This can be rewritten:







Let 




Assume Statement 1 alone. This can be rewritten:
Assume Statement 2 alone. This can be rewritten:
Compare your answer with the correct one above
A right triangle  with right angle
with right angle  ; all of its interior angles have degree measures that are whole numbers. What is the measure of
; all of its interior angles have degree measures that are whole numbers. What is the measure of  ?
?
Statement 1:  is a multiple of 2 and 7.
is a multiple of 2 and 7.
Statement 2:  is a multiple of 3 and 4.
is a multiple of 3 and 4.
A right triangle 


Statement 1: 
Statement 2: 
An acute angle must have measure less than  .
.
Assume Statement 1 alone. We are looking for a whole number that is a multiple of both 2 and 7, and is less than 90. There are several such numbers - 14 and 28, for example. There is no way of eliminating any of them, so the question is left unanswered.
Statement 2 alone provides insufficient information for similar reasons, since there are several whole numbers less than 90 that are multiples of 3 and 4 - 12 and 24, for example - with no way of eliminating any of them.
Now assume both statements to be true. 3, 4, and 7 are relatively prime - the greatest common factor of the four is 1 - so in order to find the least common multiple of the four, we need to multiply them. This product is
 ,
,
which is also a multiple of 2. Any other multiple of all four numbers must be a multiple of 84, but any other positive multiple of 84 is greater than 90. Therefore, from the two statements together, it can be deduced that  has measure
has measure  .
.
An acute angle must have measure less than 
Assume Statement 1 alone. We are looking for a whole number that is a multiple of both 2 and 7, and is less than 90. There are several such numbers - 14 and 28, for example. There is no way of eliminating any of them, so the question is left unanswered.
Statement 2 alone provides insufficient information for similar reasons, since there are several whole numbers less than 90 that are multiples of 3 and 4 - 12 and 24, for example - with no way of eliminating any of them.
Now assume both statements to be true. 3, 4, and 7 are relatively prime - the greatest common factor of the four is 1 - so in order to find the least common multiple of the four, we need to multiply them. This product is

which is also a multiple of 2. Any other multiple of all four numbers must be a multiple of 84, but any other positive multiple of 84 is greater than 90. Therefore, from the two statements together, it can be deduced that 

Compare your answer with the correct one above

In the above figure, triangle SPQ, SPR and PRQ are right triangles. Given the lengths of SP and PQ are 2cm. What is the area of triangle SPR?
In the above figure, triangle SPQ, SPR and PRQ are right triangles. Given the lengths of SP and PQ are 2cm. What is the area of triangle SPR?
Since  are right triangles, we know that
are right triangles, we know that  is an isosceles right triangle. So we know that the lengths of
is an isosceles right triangle. So we know that the lengths of  and
and  are 2 cm, so we can get the length of
are 2 cm, so we can get the length of  by using the Pythagorean Theorem:
by using the Pythagorean Theorem:

 is the midpoint of
is the midpoint of  , so the length of
, so the length of  is
is  .
.
Now we can use the Pythagorean Theorem again to solve for  :
:  .
.
Finally, we have all the elements needed to solve for the area of  :
:

Since 








Now we can use the Pythagorean Theorem again to solve for 

Finally, we have all the elements needed to solve for the area of 
Compare your answer with the correct one above
If a right triangle has a hypotenuse that is 10, and one side is 6, find the area of the triangle.
If a right triangle has a hypotenuse that is 10, and one side is 6, find the area of the triangle.
Becaue this is a right triangle and since the hypotenuse is 10 and one side is 6, the other side will be 8. This can be found using the Pythagorean Theorem, or multiplying a 3-4-5 triangle by 2 to get a 6-8-10 triangle. Since the area of a right triangle is half of the product of the two sides, we have

Becaue this is a right triangle and since the hypotenuse is 10 and one side is 6, the other side will be 8. This can be found using the Pythagorean Theorem, or multiplying a 3-4-5 triangle by 2 to get a 6-8-10 triangle. Since the area of a right triangle is half of the product of the two sides, we have
Compare your answer with the correct one above
A triangle on the coordinate plane has vertices .
.
Which of the following expressions is equal to the area of the triangle?
A triangle on the coordinate plane has vertices
Which of the following expressions is equal to the area of the triangle?
This is a right triangle with legs along the  - and
- and  -axes, so the area of each can be calculated by taking one-half the product of the two legs.
-axes, so the area of each can be calculated by taking one-half the product of the two legs.
The vertical leg has length  ; the horizontal leg has length
; the horizontal leg has length  .
.
Now calculate the area:

This is a right triangle with legs along the 

The vertical leg has length 

Now calculate the area:
Compare your answer with the correct one above
The hypotenuse of a  triangle is equal to the sidelength of a square. Give the ratio of the area of the square to that of the triangle.
triangle is equal to the sidelength of a square. Give the ratio of the area of the square to that of the triangle.
The hypotenuse of a 
Let  be the sidelength of the square. Then its area is
be the sidelength of the square. Then its area is  .
.
If the hypotenuse of a  triangle is
triangle is  , its shorter leg is half that, or
, its shorter leg is half that, or  ; its longer leg is
; its longer leg is  times the shorter leg, or
times the shorter leg, or  . The area of the triangle is half the product of the legs, or
. The area of the triangle is half the product of the legs, or

The ratio of the area of the square to that of the triangle is
 or
or 
or 
Let 

If the hypotenuse of a 




The ratio of the area of the square to that of the triangle is

or
Compare your answer with the correct one above
Calculate the area of the following right triangle, leave in terms of  .
.

(Not drawn to scale.)
Calculate the area of the following right triangle, leave in terms of 

(Not drawn to scale.)
The equation for the area of a right triangle is:

In this case, our values are: 
Plugging this into the equation leaves us with:

which can be rewritten as 
The equation for the area of a right triangle is:
In this case, our values are:
Plugging this into the equation leaves us with:
which can be rewritten as
Compare your answer with the correct one above
A right triangle has a hypotenuse of 13 and a base of 12. Calculate the area of the triangle.
A right triangle has a hypotenuse of 13 and a base of 12. Calculate the area of the triangle.
In order to calculate the area of a right triangle, we need to know the height and the base. We are only given the length of the base, so we first need to use the Pythagorean theorem with the given hypotenuse to find the length of the height:



Now that we have the height and the base, we can plug these values into the formula for the area of a right triangle:

In order to calculate the area of a right triangle, we need to know the height and the base. We are only given the length of the base, so we first need to use the Pythagorean theorem with the given hypotenuse to find the length of the height:
Now that we have the height and the base, we can plug these values into the formula for the area of a right triangle:
Compare your answer with the correct one above
Find the area of a triangle whose base is  and height is
and height is  .
.
Find the area of a triangle whose base is 

To find the area, use the following formula:

To find the area, use the following formula:
Compare your answer with the correct one above
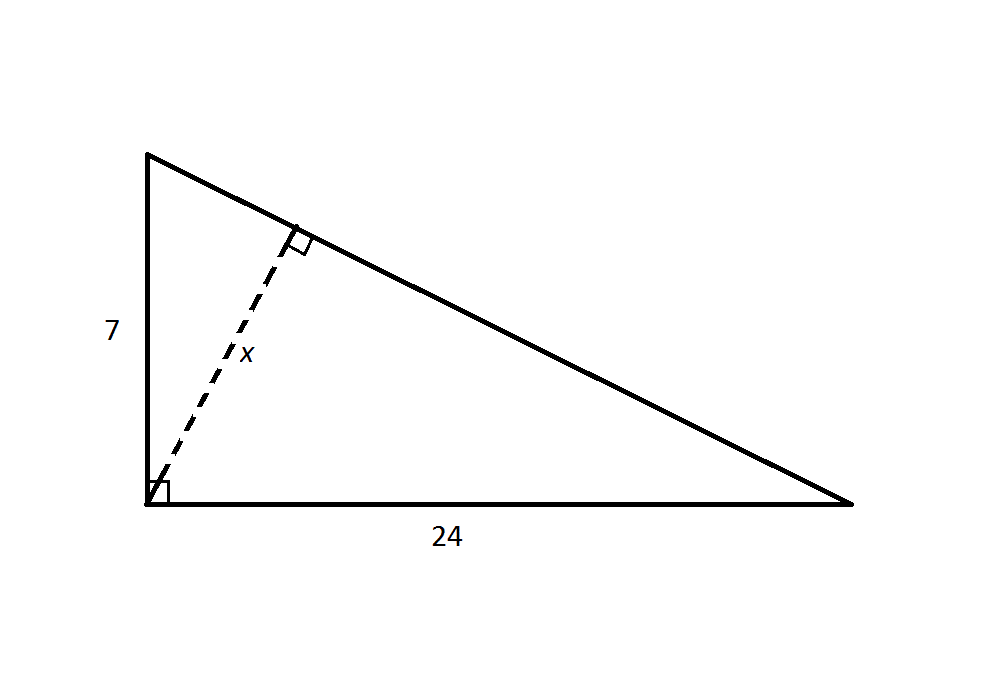
Note: Figure NOT drawn to scale
Refer to the above diagram.
Calculate 

Note: Figure NOT drawn to scale
Refer to the above diagram.
Calculate
The hypotenuse of the large right triangle is

The area of the large right triangle is half the product of its base and its height. The base can be any side of the triangle; the height would be the length of the altitude, which is the perpendicular segment from the opposite vertex to that base.
Therefore, the area of the triangle can be calculated as half the product of the legs:

Or half the product of the hypotenuse and the length  of the dashed line.
of the dashed line.

To calculate  , we can set these expressions equal to each other:
, we can set these expressions equal to each other:



The hypotenuse of the large right triangle is
The area of the large right triangle is half the product of its base and its height. The base can be any side of the triangle; the height would be the length of the altitude, which is the perpendicular segment from the opposite vertex to that base.
Therefore, the area of the triangle can be calculated as half the product of the legs:
Or half the product of the hypotenuse and the length 
To calculate 
Compare your answer with the correct one above
A right triangle has a base of 8 and an area of 24. What is the height of the triangle?
A right triangle has a base of 8 and an area of 24. What is the height of the triangle?
Using the formula for the area of a right triangle, we can plug in the given values and solve for the height of the triangle:




Using the formula for the area of a right triangle, we can plug in the given values and solve for the height of the triangle:
Compare your answer with the correct one above

Triangle  is a right triangle with
is a right triangle with  . What is the length of its height
. What is the length of its height  ?
?

Triangle 


The height AE, divides the triangle ABC, in two triangles AEC and AEB with same proportions as the original triangle ABC, this property holds true for any right triangle.
In other words,  .
.
Therefore, we can calculate, the length of AE:
 .
.
The height AE, divides the triangle ABC, in two triangles AEC and AEB with same proportions as the original triangle ABC, this property holds true for any right triangle.
In other words, 
Therefore, we can calculate, the length of AE:

Compare your answer with the correct one above

Triangle  is a right triangle with sides
is a right triangle with sides  . What is the size of the height
. What is the size of the height  ?
?

Triangle 


As we have previously seen, the height of a right triangle divides a it into two similar triangles with sides of same proportion.
Therefore, we can set up the following equality:  or
or  .
.
By plugging in the numbers, we get,  or
or  .
.
As we have previously seen, the height of a right triangle divides a it into two similar triangles with sides of same proportion.
Therefore, we can set up the following equality: 

By plugging in the numbers, we get, 

Compare your answer with the correct one above

 is a right isosceles triangle, with height
is a right isosceles triangle, with height  .
.  , what is the length of the height
, what is the length of the height  ?
?





Since here ABC is a isosceles right triangle, its height is half the size of the hypotenuse.
We just need to apply the Pythagorean Theorem to get the length of BC, and divide this length by two.
 , so
, so  .
.
Therefore,  and the final answer is
and the final answer is  .
.
Since here ABC is a isosceles right triangle, its height is half the size of the hypotenuse.
We just need to apply the Pythagorean Theorem to get the length of BC, and divide this length by two.


Therefore, 

Compare your answer with the correct one above