Tetrahedrons - GMAT Quantitative Reasoning
Card 0 of 20
The volume of a tetrahedron is  . What is the edge of the tetrahedron?
. What is the edge of the tetrahedron?
The volume of a tetrahedron is 
Write the formula to solve for the edge of a tetrahedron.
![e=\sqrt2 \sqrt[3]{3V}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/317675/gif.latex)
Substitute the given volume to the equation and solve.
![e=\sqrt2 \sqrt[3]{3(9)}= \sqrt2 \sqrt[3]{27}=3\sqrt2](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/317676/gif.latex)
Write the formula to solve for the edge of a tetrahedron.
Substitute the given volume to the equation and solve.
Compare your answer with the correct one above
Suppose the volume of the tetrahedron is  . What is the edge of the tetrahedron?
. What is the edge of the tetrahedron?
Suppose the volume of the tetrahedron is 
Write the formula to solve for the edge of a tetrahedron.
![e=\sqrt2 \sqrt[3]{3V}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/317568/gif.latex)
Substitute the volume and solve.
![e=\sqrt2 \sqrt[3]{3(\frac{1}{3})}= \sqrt2 \sqrt[3]{1}=\sqrt2](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/317569/gif.latex)
Write the formula to solve for the edge of a tetrahedron.
Substitute the volume and solve.
Compare your answer with the correct one above
Find the exact edge length of a tetrahedron if the volume is  .
.
Find the exact edge length of a tetrahedron if the volume is 
Write the tetrahedron formula to solve for the edge.
![e=\sqrt2 \sqrt[3]{3V}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/317627/gif.latex)
Substitute the volume and simplify.
![e=\sqrt2 \sqrt[3]{3(3)}= \sqrt2 \sqrt[3]{9}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/317628/gif.latex)
Write the tetrahedron formula to solve for the edge.
Substitute the volume and simplify.
Compare your answer with the correct one above
The height of one of the equilateral triangle faces on a tetrahedron is  . What is the side length of the tetrahedron?
. What is the side length of the tetrahedron?
The height of one of the equilateral triangle faces on a tetrahedron is 
Because a tetrahedron has four congruent equilateral triangles as its faces, we know the three equal angles of each face, as with all equilateral triangles, are each  . We are given the height of a face, which is the length of a line that bisects one of the
. We are given the height of a face, which is the length of a line that bisects one of the  angles and forms a right triangle with the side length as its hypotenuse. This means the angle between the height and the side length is
angles and forms a right triangle with the side length as its hypotenuse. This means the angle between the height and the side length is  , whose cosine is equal to the adjacent side, the height, over the hypotenuse, the side length. This gives us:
, whose cosine is equal to the adjacent side, the height, over the hypotenuse, the side length. This gives us:



Because a tetrahedron has four congruent equilateral triangles as its faces, we know the three equal angles of each face, as with all equilateral triangles, are each 


Compare your answer with the correct one above
A certain tetrahedron has a surface area of  . What is the length of an edge of the tetrahedron?
. What is the length of an edge of the tetrahedron?
A certain tetrahedron has a surface area of 
A tetrahedron has four congruent equilateral triangle faces, so its surface area is four times the area of one of these equilateral triangles. This gives us:

Where  is the base of the triangle, or the edge length of the tetrahedron, and
is the base of the triangle, or the edge length of the tetrahedron, and  is the height of each triangular face. We want to solve for
is the height of each triangular face. We want to solve for  , but we are only given the surface area and not the height, so we need to express this value in terms of the base. One way of doing this is by recognizing that the height of each equilateral triangle face bisects an angle and forms two congruent right triangles for which it is the base and the edge length, or
, but we are only given the surface area and not the height, so we need to express this value in terms of the base. One way of doing this is by recognizing that the height of each equilateral triangle face bisects an angle and forms two congruent right triangles for which it is the base and the edge length, or  , is the hypotenuse. Each angle in an equilateral triangle is
, is the hypotenuse. Each angle in an equilateral triangle is  , so if one is bisected by the height then the angle between it and the hypotenuse is
, so if one is bisected by the height then the angle between it and the hypotenuse is  . The cosine of this angle is equal to the height over the hypotenuse, which gives us:
. The cosine of this angle is equal to the height over the hypotenuse, which gives us:

Now that we have an expression for the height in terms of the base, we can plug this value into the equation for surface area and be left with only one unknown, the base that is equivalent to the edge length for which we want to solve:



A tetrahedron has four congruent equilateral triangle faces, so its surface area is four times the area of one of these equilateral triangles. This gives us:
Where 





Now that we have an expression for the height in terms of the base, we can plug this value into the equation for surface area and be left with only one unknown, the base that is equivalent to the edge length for which we want to solve:
Compare your answer with the correct one above
In three-dimensional space, the four vertices of a tetrahedron - a solid with four faces - have Cartesian coordinates  .
.
Give the surface area of the tetrahedron.
In three-dimensional space, the four vertices of a tetrahedron - a solid with four faces - have Cartesian coordinates 
Give the surface area of the tetrahedron.
The tetrahedron looks like this:

 is the origin and
is the origin and  are the other three points, which are 60 units away from the origin on each of the three (perpendicular) axes.
are the other three points, which are 60 units away from the origin on each of the three (perpendicular) axes.
The bottom, front, and left faces are each right triangles whose legs each measure 60. Each face has area
 .
.
The remaining face has three edges each a hypotenuse of one of three congruent right triangles, so its sides are congruent, and it is an equilateral triangle. Its sidelength can be found via the 45-45-90 Theorem to be  , so its area is
, so its area is

The total area is

The tetrahedron looks like this:



The bottom, front, and left faces are each right triangles whose legs each measure 60. Each face has area

The remaining face has three edges each a hypotenuse of one of three congruent right triangles, so its sides are congruent, and it is an equilateral triangle. Its sidelength can be found via the 45-45-90 Theorem to be 
The total area is
Compare your answer with the correct one above
The slant height of a pyramid is one and one-half times the perimeter of its square base. The base has sides of length 15 inches. What is the surface area of the pyramid?
The slant height of a pyramid is one and one-half times the perimeter of its square base. The base has sides of length 15 inches. What is the surface area of the pyramid?
The square base of the pyramid has four sides with length 15 inches, making its perimeter four times that, or 60 inches. The slant height is
 inches.
inches.
Therefore, the area of the base is  square inches.
square inches.
Each of the four lateral triangles has area  square inches.
square inches.
The total surface area is  square inches.
square inches.
The square base of the pyramid has four sides with length 15 inches, making its perimeter four times that, or 60 inches. The slant height is

Therefore, the area of the base is 
Each of the four lateral triangles has area 
The total surface area is 
Compare your answer with the correct one above
A regular tetrahedron comprises four faces, each of which is an equilateral triangle. If the sum of the lengths of its edges is 120, what is its surface area?
A regular tetrahedron comprises four faces, each of which is an equilateral triangle. If the sum of the lengths of its edges is 120, what is its surface area?
As shown in the diagram below, a regular tetrahedron has six congruent edges, so each has length  :
:

The area of one face is the area of an equilateral triangle with sidelength 20, which is

The total surface area is four times this, or  .
.
As shown in the diagram below, a regular tetrahedron has six congruent edges, so each has length 

The area of one face is the area of an equilateral triangle with sidelength 20, which is
The total surface area is four times this, or 
Compare your answer with the correct one above

Refer to the above diagram, which shows a tetrahedron.
 , and
, and  . Give the surface area of the tetrahedron.
. Give the surface area of the tetrahedron.

Refer to the above diagram, which shows a tetrahedron.


Three of the surfaces of the tetrahedron -  ,
,  , and
, and  - are isosceles right triangles with hypotenuse 30, so by the 45-45-90 Theorem, each leg measures this length divided by
- are isosceles right triangles with hypotenuse 30, so by the 45-45-90 Theorem, each leg measures this length divided by  , or
, or
 .
.
The area of each of these triangles is half the product of its legs, so each area is

Also, the legs are of the same measure among the triangles, the hypotenuses are as well, so the fourth surface  is an equilateral triangle. Its sidelength is
is an equilateral triangle. Its sidelength is  , so we use the equilateral triangle area formula to calculate its area:
, so we use the equilateral triangle area formula to calculate its area:

Add the areas of the faces:

Three of the surfaces of the tetrahedron - 




The area of each of these triangles is half the product of its legs, so each area is
Also, the legs are of the same measure among the triangles, the hypotenuses are as well, so the fourth surface 

Add the areas of the faces:
Compare your answer with the correct one above
A regular tetrahedron is a solid with four faces, each of which is an equilateral triangle.
If the lengths of all of the edges of a regular tetrahedron are added, the total length is 120. What is the surface area of the tetrahedron?
A regular tetrahedron is a solid with four faces, each of which is an equilateral triangle.
If the lengths of all of the edges of a regular tetrahedron are added, the total length is 120. What is the surface area of the tetrahedron?
A tetrahedron looks like this:

The tetrahedron has six edges, and in a regular tetrahedron, they are congruent, so each edge has length  .
.
The area of one face of the tetrahedron, it being an equilateral triangle, can be calulated using the formula

There are four congruent faces, so the total surface area is

Since  , the surface area of the tetrahedron is
, the surface area of the tetrahedron is

A tetrahedron looks like this:

The tetrahedron has six edges, and in a regular tetrahedron, they are congruent, so each edge has length 
The area of one face of the tetrahedron, it being an equilateral triangle, can be calulated using the formula
There are four congruent faces, so the total surface area is
Since 
Compare your answer with the correct one above
A regular tetrahedron is a solid with four faces, each of which is an equilateral triangle.
Each edge of a regular tetrahedron has length  . What is the surface area of the tetrahedron?
. What is the surface area of the tetrahedron?
A regular tetrahedron is a solid with four faces, each of which is an equilateral triangle.
Each edge of a regular tetrahedron has length 
The area of one face of the tetrahedron, it being an equilateral triangle, can be calulated using the formula

There are four congruent faces, so the total surface area is

Since  , the surface area of the tetrahedron is
, the surface area of the tetrahedron is

The area of one face of the tetrahedron, it being an equilateral triangle, can be calulated using the formula
There are four congruent faces, so the total surface area is
Since 
Compare your answer with the correct one above

Evaluate the surface area of the above tetrahedron.

Evaluate the surface area of the above tetrahedron.
Three of the faces of the tetrahedron are isosceles right triangles with legs of length 8, and, subsequently, by the 45-45-90 Theorem, hypotenuses of length  . The fourth face, consequently, is an equilateral triangle with three sides of length
. The fourth face, consequently, is an equilateral triangle with three sides of length  .
.
Each of the three right triangle faces has area equal to half the product of its legs , which is
 .
.
The equilateral face has as its area






The sum of the areas of the faces is

Three of the faces of the tetrahedron are isosceles right triangles with legs of length 8, and, subsequently, by the 45-45-90 Theorem, hypotenuses of length 

Each of the three right triangle faces has area equal to half the product of its legs , which is

The equilateral face has as its area
The sum of the areas of the faces is
Compare your answer with the correct one above

The cube in the above figure has surface area 384. Give the surface area of the tetrahedron with vertices  , shown in red.
, shown in red.

The cube in the above figure has surface area 384. Give the surface area of the tetrahedron with vertices 
The surface area formula can be used to find the length of each edge of the cube:


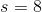
Three faces of the tetrahedron -  ,
, 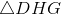 ,
,  - are right triangles with legs of length 8, so the area of each is half the product of the lengths of their legs:
- are right triangles with legs of length 8, so the area of each is half the product of the lengths of their legs:
 .
.
Each triangle is isosceles, so, by the 45-45-90 Theorem, each of their hypotentuses measures  times a leg, or
times a leg, or  . is therefore an equilateral triangle with sidelenghth
. is therefore an equilateral triangle with sidelenghth  . Its area can be found as follows:
. Its area can be found as follows:


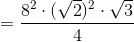

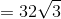
The total surface area is

The surface area formula can be used to find the length of each edge of the cube:
Three faces of the tetrahedron - 
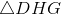


Each triangle is isosceles, so, by the 45-45-90 Theorem, each of their hypotentuses measures 


The total surface area is
Compare your answer with the correct one above

The above diagram shows a regular right triangular pyramid. Its base  is an equilateral triangle; the other three faces are congruent isosceles triangles, with
is an equilateral triangle; the other three faces are congruent isosceles triangles, with  an altitude of
an altitude of  . Give the surface area of the pyramid.
. Give the surface area of the pyramid.

The above diagram shows a regular right triangular pyramid. Its base 


The base is an equilateral triangle with sidelength 12, so its area can be calculated as follows:
 .
.
Each of the three other faces is congruent, with base 12. The area of each is the product of its base and its height. To find the common height, we examine  , which, since
, which, since  is an altitude of isosceles
is an altitude of isosceles  , is a right triangle with hypotenuse of length 18 and one leg of length
, is a right triangle with hypotenuse of length 18 and one leg of length  . We can find
. We can find  using the Pythagorean Theorem:
using the Pythagorean Theorem:





The area of  is half the product of this height and the base:
is half the product of this height and the base:

All three lateral faces have this area.
Now add the areas of the four faces:

The base is an equilateral triangle with sidelength 12, so its area can be calculated as follows:

Each of the three other faces is congruent, with base 12. The area of each is the product of its base and its height. To find the common height, we examine 




The area of 
All three lateral faces have this area.
Now add the areas of the four faces:
Compare your answer with the correct one above
What is the volume of a right pyramid whose height is 20 and whose base is an equilateral triangle with sidelength 10?
What is the volume of a right pyramid whose height is 20 and whose base is an equilateral triangle with sidelength 10?
The volume of a pyramid can be calculated using the formula

where  is the height and
is the height and  is the area of the base.
is the area of the base.
Since the base is an equilateral triangle, its area can be calculated using the formula

Therefore, the volume can be rewritten as

Substitute  :
:




The volume of a pyramid can be calculated using the formula
where 

Since the base is an equilateral triangle, its area can be calculated using the formula
Therefore, the volume can be rewritten as
Substitute 
Compare your answer with the correct one above
A right triangular pyramid has as its base an equilateral triangle with sidelength 10. Its height is 15.
Give its volume.
A right triangular pyramid has as its base an equilateral triangle with sidelength 10. Its height is 15.
Give its volume.
The base of the triangle has an area that can be found using the formula for the area of an equilateral triangle, substituting  :
:




Now, in the formula for the volume of a pyramid, substitute  :
:



The base of the triangle has an area that can be found using the formula for the area of an equilateral triangle, substituting 
Now, in the formula for the volume of a pyramid, substitute 
Compare your answer with the correct one above
The height of a right pyramid and the sidelength of its square base are equal. The perimeter of the base is one yard. Give its volume in cubic inches.
The height of a right pyramid and the sidelength of its square base are equal. The perimeter of the base is one yard. Give its volume in cubic inches.
The perimeter of the base is one yard, or 36 inches; its sidelength - and, sunsequently, its height - are one-fourth of that, or 9 inches, and the area of the base is  square inches. The volume of a pyramid is one-third the product of its height and the area of its base, so substitute
square inches. The volume of a pyramid is one-third the product of its height and the area of its base, so substitute  in the following:
in the following:
 cubic inches.
cubic inches.
The perimeter of the base is one yard, or 36 inches; its sidelength - and, sunsequently, its height - are one-fourth of that, or 9 inches, and the area of the base is 


Compare your answer with the correct one above
In three-dimensional space, the four vertices of a tetrahedron - a solid with four faces - have Cartesian coordinates  .
.
What is the volume of this tetrahedron?
In three-dimensional space, the four vertices of a tetrahedron - a solid with four faces - have Cartesian coordinates 
What is the volume of this tetrahedron?
The tetrahedron looks like this:

 is the origin and
is the origin and  are the other three points, which are 60 units away from the origin on each of the three (mutually perpendicular) axes.
are the other three points, which are 60 units away from the origin on each of the three (mutually perpendicular) axes.
This is a triangular pyramid, and we can consider  the (right triangular) base; its area is half the product of its legs, or
the (right triangular) base; its area is half the product of its legs, or
 .
.
The volume of the tetrahedron is one third the product of its base and its height, the latter of which is 60. Therefore,
 .
.
The tetrahedron looks like this:



This is a triangular pyramid, and we can consider 

The volume of the tetrahedron is one third the product of its base and its height, the latter of which is 60. Therefore,

Compare your answer with the correct one above
In three-dimensional space, the four vertices of a tetrahedron - a solid with four faces - have Cartesian coordinates  .
.
Give its volume.
In three-dimensional space, the four vertices of a tetrahedron - a solid with four faces - have Cartesian coordinates 
Give its volume.
A tetrahedron is a triangular pyramid and can be looked at as such.
Three of the vertices -  - are on the
- are on the  -plane, and can be seen as the vertices of the triangular base. This triangle, as seen below, is isosceles:
-plane, and can be seen as the vertices of the triangular base. This triangle, as seen below, is isosceles:

Its base is 60 and its height is 40, so its area is

The fourth vertex is off the  -plane; its perpendicular distance to the aforementioned face is its
-plane; its perpendicular distance to the aforementioned face is its  -coordinate, 20, so this is the height of the pyramid. The volume of the pyramid is
-coordinate, 20, so this is the height of the pyramid. The volume of the pyramid is
 .
.
A tetrahedron is a triangular pyramid and can be looked at as such.
Three of the vertices - 


Its base is 60 and its height is 40, so its area is
The fourth vertex is off the 


Compare your answer with the correct one above
In three-dimensional space, the four vertices of a tetrahedron - a solid with four faces - have Cartesian coordinates
 ,
,
where 
Give its volume in terms of  .
.
In three-dimensional space, the four vertices of a tetrahedron - a solid with four faces - have Cartesian coordinates

where
Give its volume in terms of 
The tetrahedron looks like this:

 is the origin and
is the origin and  are the other three points, whose distances away from the origin on each of the three (perpendicular) axes are shown.
are the other three points, whose distances away from the origin on each of the three (perpendicular) axes are shown.
This is a triangular pyramid, and we can consider  the (right triangular) base; its area is half the product of its legs, or
the (right triangular) base; its area is half the product of its legs, or
 .
.
The volume of the tetrahedron is one third the product of its base and its height, the latter of which is  . Therefore,
. Therefore,
 .
.
The tetrahedron looks like this:



This is a triangular pyramid, and we can consider 

The volume of the tetrahedron is one third the product of its base and its height, the latter of which is 

Compare your answer with the correct one above