Other Quadrilaterals - GMAT Quantitative Reasoning
Card 0 of 20
Is parallelogram  a rectangle?
a rectangle?
Statement 1: 
Statement 2: 
Is parallelogram 
Statement 1:
Statement 2:
Any two consecutive angles of a parallelogram are supplementary, so if one angle has measure  , all angles can be proven to have measure
, all angles can be proven to have measure  . This is the definition of a rectangle. Statement 1 therefore proves the parallelogram to be a rectangle.
. This is the definition of a rectangle. Statement 1 therefore proves the parallelogram to be a rectangle.
Also, a parallelogram is a rectangle if and only if its diagonals are congruent, which is what Statement 2 asserts.
From either statement, it follows that parallelogram  is a rectangle.
is a rectangle.
Any two consecutive angles of a parallelogram are supplementary, so if one angle has measure 

Also, a parallelogram is a rectangle if and only if its diagonals are congruent, which is what Statement 2 asserts.
From either statement, it follows that parallelogram 
Compare your answer with the correct one above
Given a quadrilateral  , can a circle be circumscribed about it?
, can a circle be circumscribed about it?
Statement 1: Quadrilateral  is not a rectangle.
is not a rectangle.
Statement 2: 
Given a quadrilateral 
Statement 1: Quadrilateral 
Statement 2:
A circle can be circumscribed about a quadrilateral if and only if both pairs of opposite angles are supplementary. This is not proved or disproved by Statement 1 alone:
Case 1: 
This is not a rectangle, and opposite angles are supplementary, so a circle can be constructed to circumscribe the quadrilateral.
Case 2: 
This is not a rectangle, and opposite angles are not supplementary, so a circle cannot be constructed to circumscribe the quadrilateral.
From Statement 2, however, it follows that a two opposite angles are not a supplementary pair, so a circle cannot be circumscribed about it.
A circle can be circumscribed about a quadrilateral if and only if both pairs of opposite angles are supplementary. This is not proved or disproved by Statement 1 alone:
Case 1:
This is not a rectangle, and opposite angles are supplementary, so a circle can be constructed to circumscribe the quadrilateral.
Case 2:
This is not a rectangle, and opposite angles are not supplementary, so a circle cannot be constructed to circumscribe the quadrilateral.
From Statement 2, however, it follows that a two opposite angles are not a supplementary pair, so a circle cannot be circumscribed about it.
Compare your answer with the correct one above
Given a quadrilateral  , can a circle be circumscribed about it?
, can a circle be circumscribed about it?
Statement 1: Quadrilateral  is an isosceles trapezoid.
is an isosceles trapezoid.
Statement 2: 
Given a quadrilateral 
Statement 1: Quadrilateral 
Statement 2:
A circle can be circumscribed about a quadrilateral if and only if both pairs of its opposite angles are supplementary.
An isosceles trapezoid has this characteristic. Assume without loss of generality that  and
and  are the pairs of base angles.
are the pairs of base angles.
Then, since base angles are congruent,  and
and  . Since the bases of a trapezoid are parallel, from the Same-Side Interior Angles Theorem,
. Since the bases of a trapezoid are parallel, from the Same-Side Interior Angles Theorem,  and
and  are supplementary, and, subsequently, so are
are supplementary, and, subsequently, so are  and
and  , as well as
, as well as  and
and  .
.
If  , then
, then  and
and  form a supplementary pair, as their measures total
form a supplementary pair, as their measures total  ; since the measures of the angles of a quadrilateral total
; since the measures of the angles of a quadrilateral total  , the measures of
, the measures of  and
and  also total
also total  , making them supplementary as well.
, making them supplementary as well.
Therefore, it follows from either statement that both pairs of opposite angles are supplementary, and that a circle can be circumscribed about the quadrilateral.
A circle can be circumscribed about a quadrilateral if and only if both pairs of its opposite angles are supplementary.
An isosceles trapezoid has this characteristic. Assume without loss of generality that 

Then, since base angles are congruent, 







If 







Therefore, it follows from either statement that both pairs of opposite angles are supplementary, and that a circle can be circumscribed about the quadrilateral.
Compare your answer with the correct one above
Given Parallelogram  .
.
True or false: 
Statement 1: 
Statement 2: 
Given Parallelogram 
True or false:
Statement 1:
Statement 2:
 and
and  , the diagonals of Parallelogram
, the diagonals of Parallelogram  , are perpendicular if and only if Parallelogram
, are perpendicular if and only if Parallelogram  is also a rhombus.
is also a rhombus.
Opposite sides of a parallelogram are congruent, so if Statement 1 is assumed,  . Parallelogram
. Parallelogram  a rhombus; subsequently,
a rhombus; subsequently,  .
.
The angle measures are irrelevant, so Statement 2 is unhelpful.




Opposite sides of a parallelogram are congruent, so if Statement 1 is assumed, 


The angle measures are irrelevant, so Statement 2 is unhelpful.
Compare your answer with the correct one above
Are the diagonals of Quadrilateral  perpendicular?
perpendicular?
(a) 
(b) 
Are the diagonals of Quadrilateral 
(a)
(b)
For the diagonals of a quadrilateral to be perpendicular, the quadrilateral must be a kite or a rhombus - in either case, there must be two pairs of adjacent congruent sides. Neither statement alone proves this, but both statements together do.
For the diagonals of a quadrilateral to be perpendicular, the quadrilateral must be a kite or a rhombus - in either case, there must be two pairs of adjacent congruent sides. Neither statement alone proves this, but both statements together do.
Compare your answer with the correct one above
Quadrilateral  is inscribed in a circle.
is inscribed in a circle.
What is  ?
?
Statement 1: 
Statement 2: 
Quadrilateral 
What is 
Statement 1:
Statement 2:
From Statement 1 alone, we can calculate  , since two opposite angles of a quadrilateral inscribed inside a circle are supplementary:
, since two opposite angles of a quadrilateral inscribed inside a circle are supplementary:

From Statement 2 alone, we can calculate  , since the degree measure of an inscribed angle of a circle is half that of the arc it intersects:
, since the degree measure of an inscribed angle of a circle is half that of the arc it intersects:

From Statement 1 alone, we can calculate 
From Statement 2 alone, we can calculate 
Compare your answer with the correct one above

The above shows Parallelogram  . Is it a rectangle?
. Is it a rectangle?
Statement 1: 
Statement 2: 

The above shows Parallelogram 
Statement 1:
Statement 2:
To prove that Parallelogram  is also a rectangle, we need to prove that any one of its angles is a right angle.
is also a rectangle, we need to prove that any one of its angles is a right angle.
If we assume Statement 1 alone, that  , then, since
, then, since  and
and  form a linear pair,
form a linear pair,  is right.
is right.
If we assume Statement 2 alone, that  , it follows from the converse of the Pythagorean Theorem that
, it follows from the converse of the Pythagorean Theorem that  is a right triangle with right angle
is a right triangle with right angle  .
.
Either way, we have proved that the parallelogram is a rectangle.
To prove that Parallelogram 
If we assume Statement 1 alone, that 



If we assume Statement 2 alone, that 


Either way, we have proved that the parallelogram is a rectangle.
Compare your answer with the correct one above

Refer to the above figure. You are given that Polygon  is a parallelogram but not that it is a rectangle. Is it a rectangle?
is a parallelogram but not that it is a rectangle. Is it a rectangle?
Statement 1: 
Statement 2:  and
and  are complementary angles.
are complementary angles.

Refer to the above figure. You are given that Polygon 
Statement 1:
Statement 2: 

It is necessary and sufficient to prove that one of the angles of the parallelogram is a right angle.
Assume Statement 1 alone - that  .
.  and
and  are supplementary, since they are same-side interior angles of parallel lines. Since
are supplementary, since they are same-side interior angles of parallel lines. Since  ,
,  is also supplementary to
is also supplementary to  . But as corresponding angles of parallel lines,
. But as corresponding angles of parallel lines,  . Two angles that are conruent and supplementary are both right angles, so
. Two angles that are conruent and supplementary are both right angles, so  is a right angle.
is a right angle.
Assume Statement 2 alone - that  and
and  are complementary angles, or, equivalently,
are complementary angles, or, equivalently,  . Since the angles of a triangle have measures that add up to
. Since the angles of a triangle have measures that add up to  , the third angle of
, the third angle of  , which is
, which is  , measures
, measures  , and is a right angle.
, and is a right angle.
Either statement alone proves  a right angle and subsequently proves
a right angle and subsequently proves  a rectangle.
a rectangle.
It is necessary and sufficient to prove that one of the angles of the parallelogram is a right angle.
Assume Statement 1 alone - that 







Assume Statement 2 alone - that 






Either statement alone proves 

Compare your answer with the correct one above
True or false: Quadrilateral  is a rectangle.
is a rectangle.
Statement 1: 
Statement 2: 
True or false: Quadrilateral 
Statement 1:
Statement 2:
Assume Statement 1 alone. By congruence,  and
and  , making Quadrilateral
, making Quadrilateral  a parallelogram. However, no clue is given to whether any angles are right or not, so whether the quadrilateral is a rectangle or not remains open.
a parallelogram. However, no clue is given to whether any angles are right or not, so whether the quadrilateral is a rectangle or not remains open.
Assume Statement 2 alone. By congruence, opposite sides  , but no clue is provided as to the lengths of opposite sides
, but no clue is provided as to the lengths of opposite sides  and
and  . Also,
. Also,  , but no clue is provided as to whether the angles are right. A rectangle would have both characteristics, but so would an isosceles trapezoid with legs
, but no clue is provided as to whether the angles are right. A rectangle would have both characteristics, but so would an isosceles trapezoid with legs  and
and  .
.
Assume both statements are true. Quadrilateral  is a parallelogram as a consequence of Statement 1. Since
is a parallelogram as a consequence of Statement 1. Since  and
and  are consecutive angles of the parallelogram, they are supplementary, but they are also congruent as a consequence of Statement 2. Therefore, they are right angles, and a parallelogram with right angles is a rectangle.
are consecutive angles of the parallelogram, they are supplementary, but they are also congruent as a consequence of Statement 2. Therefore, they are right angles, and a parallelogram with right angles is a rectangle.
Assume Statement 1 alone. By congruence, 


Assume Statement 2 alone. By congruence, opposite sides 





Assume both statements are true. Quadrilateral 


Compare your answer with the correct one above
True or false: Quadrilateral  is a rectangle.
is a rectangle.
Statement 1:  and
and  are right angles.
are right angles.
Statement 2: 
True or false: Quadrilateral 
Statement 1: 

Statement 2:
Statement 1 alone is insufficient to answer the question; A quadrilateral in which  and
and  are right angles,
are right angles,  , and
, and  fits the statement, as well as a rectangle, which by defintion has four right angles.
fits the statement, as well as a rectangle, which by defintion has four right angles.
Statement 2 alone is insufficient as well, as a parallelogram with acute and obtuse angles, as well as a rectangle, fits the description.
Assume both statements, and construct diagonal  to form two triangles
to form two triangles  and
and  . By Statement 1, both triangles are right with congruent legs
. By Statement 1, both triangles are right with congruent legs  , and congruent hypotenuses, both being the same segment
, and congruent hypotenuses, both being the same segment  . By the Hypotenuse Leg Theorem,
. By the Hypotenuse Leg Theorem,  . By congruence,
. By congruence,  . The quadrilateral, having two sets of congruent opposite sides, is a parallelogram; a parallelogram with right angles is a rectangle.
. The quadrilateral, having two sets of congruent opposite sides, is a parallelogram; a parallelogram with right angles is a rectangle.
Statement 1 alone is insufficient to answer the question; A quadrilateral in which 



Statement 2 alone is insufficient as well, as a parallelogram with acute and obtuse angles, as well as a rectangle, fits the description.
Assume both statements, and construct diagonal 






Compare your answer with the correct one above
Consider rectangle  .
.
I) Side  is
is  fathoms long.
fathoms long.
II) Side  is three fourths of
is three fourths of  .
.
What is the length segment  , the diagonal of
, the diagonal of  ?
?
Consider rectangle 
I) Side 

II) Side 

What is the length segment 

To find the diagonal of a rectangle, we need the length of two sides.
I) Gives us the length of one side.
II) Lets us find the length of the next side.
Use I) and II) with Pythagorean Theorem to find the diagonal.


Conversely, recognize that we are making a 3/4/5 Pythagorean Triple and see that the last side is 30 fathoms.
To find the diagonal of a rectangle, we need the length of two sides.
I) Gives us the length of one side.
II) Lets us find the length of the next side.
Use I) and II) with Pythagorean Theorem to find the diagonal.
Conversely, recognize that we are making a 3/4/5 Pythagorean Triple and see that the last side is 30 fathoms.
Compare your answer with the correct one above
Find the diagonal of a square.
Statement 1: The perimeter of the square is known.
Statement 2: A secondary square with a known area encloses the primary square where all 4 corners of the primary square touch each of secondary square's edges.
Find the diagonal of a square.
Statement 1: The perimeter of the square is known.
Statement 2: A secondary square with a known area encloses the primary square where all 4 corners of the primary square touch each of secondary square's edges.
Statement 1: The perimeter of the square is known.
A square has four equal sides. Write the perimeter formula for squares.

The side length of a square is a fourth of the perimeter.
Statement 2: A secondary square with a known area encloses the primary square where all 4 corners of the primary square touch each of secondary square's edges.
If the primary square corners touch each of the secondary square edges, they must touch at the midpoint of each edge. Since Statement 2 mentions that the secondary square area is known, it is possible to solve for the edge length and the diagonal of the secondary square. Write the formula for the area of a square.

The diagonal of the secondary square can be solved by using the Pythagorean Theorem.
The side length of the secondary square also must equal the diagonal of the primary square.
Therefore:

Statement 1: The perimeter of the square is known.
A square has four equal sides. Write the perimeter formula for squares.
The side length of a square is a fourth of the perimeter.
Statement 2: A secondary square with a known area encloses the primary square where all 4 corners of the primary square touch each of secondary square's edges.
If the primary square corners touch each of the secondary square edges, they must touch at the midpoint of each edge. Since Statement 2 mentions that the secondary square area is known, it is possible to solve for the edge length and the diagonal of the secondary square. Write the formula for the area of a square.
The diagonal of the secondary square can be solved by using the Pythagorean Theorem.
The side length of the secondary square also must equal the diagonal of the primary square.
Therefore:
Compare your answer with the correct one above

What are the lengths of the diagonals in the parallelogram  ?
?
-

-


What are the lengths of the diagonals in the parallelogram 
Each of the statements, 1 and 2, provide something integral to calculating the length of a diagonal: an angle and the length of the sides connected to its vertex. The diagonal would be the third leg of the resulting triangle, and can be calculated using the law of cosines:

Since this is a parellelogram, knowing one angle allows us to know all the angles.
Each of the statements, 1 and 2, provide something integral to calculating the length of a diagonal: an angle and the length of the sides connected to its vertex. The diagonal would be the third leg of the resulting triangle, and can be calculated using the law of cosines:
Since this is a parellelogram, knowing one angle allows us to know all the angles.
Compare your answer with the correct one above

For the parellogram  , the longest diagonal is
, the longest diagonal is  . Is
. Is  ?
?
-
The area of  is
is 
-
The perimeter of  is
is 

For the parellogram 


-
The area of
is
-
The perimeter of
is
Area alone is not enough information. Imagine, for instance, a parallelogram with a shorter side of  and a longer side of
and a longer side of  . The diagonal would be well above
. The diagonal would be well above 
However, with the perimeter, the smaller and larger sides must add up to one half of it,  .
.
The longer diagonal reaches its maximum with the larger internal angle widens towards  degrees, and the parallelogram flattens into a line. Using the law of cosines, this translates to:
degrees, and the parallelogram flattens into a line. Using the law of cosines, this translates to:


 .
.
At its max, the diagonal could be no greater than 
Area alone is not enough information. Imagine, for instance, a parallelogram with a shorter side of 

However, with the perimeter, the smaller and larger sides must add up to one half of it, 
The longer diagonal reaches its maximum with the larger internal angle widens towards 

At its max, the diagonal could be no greater than
Compare your answer with the correct one above
Find the length of the diagonal of a square.
Statement 1: The area is 1.
Statement 2: The square is inscribed inside of a circle with all 4 corners touching the edge of the circle, and the circle has an area of 1.
Find the length of the diagonal of a square.
Statement 1: The area is 1.
Statement 2: The square is inscribed inside of a circle with all 4 corners touching the edge of the circle, and the circle has an area of 1.
Statement 1: The area is 1.
Given the area of a square is sufficient to find the diagonal of the square. The formula to find the side length of the square is:

The Pythagorean theorem can then be used to solve for the length of the diagonal.
Statement 2: The square is inscribed inside of a circle with all 4 corners touching the edge of the circle, and the circle has an area of 1.
This statement is also sufficient to solve for the diagonal. With all 4 corners of the square touching the circle, the diagonal of the square is simply the length from one of the square's opposing 90 degree angles to its opposite angle, which is the diameter of the circle.
Given the area of the circle, use the formula  to determine the diameter of the circle, which is also the diagonal of the square.
to determine the diameter of the circle, which is also the diagonal of the square.
Therefore:

Statement 1: The area is 1.
Given the area of a square is sufficient to find the diagonal of the square. The formula to find the side length of the square is:
The Pythagorean theorem can then be used to solve for the length of the diagonal.
Statement 2: The square is inscribed inside of a circle with all 4 corners touching the edge of the circle, and the circle has an area of 1.
This statement is also sufficient to solve for the diagonal. With all 4 corners of the square touching the circle, the diagonal of the square is simply the length from one of the square's opposing 90 degree angles to its opposite angle, which is the diameter of the circle.
Given the area of the circle, use the formula 
Therefore:
Compare your answer with the correct one above

For rectangle PQRS, the ratio of PQ to QR is 2 to 3. What is the length of SQ?
(1) The length of PS is 9.
(2) The length of SR is 6.

For rectangle PQRS, the ratio of PQ to QR is 2 to 3. What is the length of SQ?
(1) The length of PS is 9.
(2) The length of SR is 6.
With a ratio of sides of 2:3, statement 1 tells us PS and QR are 9 units long. Knowing the ratio we can determine both PQ and SR are 6. Since rectangles have four 90 degree angles, we can use the Pythagorean Theorem to solve for the length of SQ:  . Therefore, statement 1 alone is sufficient.
. Therefore, statement 1 alone is sufficient.
With a ratio of sides of 2:3, statement 2 tells us PQ and SR are 6 units long. Knowing the ratio we can determine both PS and QR are 9 units long. Since rectangles have four 90 degree angles, we can use the Pythagorean Theorem to solve for the length of SQ:  . Therefore, statement 2 alone is sufficient.
. Therefore, statement 2 alone is sufficient.
Therefore, the correct answer is EACH statement ALONE is sufficient.
With a ratio of sides of 2:3, statement 1 tells us PS and QR are 9 units long. Knowing the ratio we can determine both PQ and SR are 6. Since rectangles have four 90 degree angles, we can use the Pythagorean Theorem to solve for the length of SQ: 
With a ratio of sides of 2:3, statement 2 tells us PQ and SR are 6 units long. Knowing the ratio we can determine both PS and QR are 9 units long. Since rectangles have four 90 degree angles, we can use the Pythagorean Theorem to solve for the length of SQ: 
Therefore, the correct answer is EACH statement ALONE is sufficient.
Compare your answer with the correct one above

For parallelogram ABCD, what is the length of AC?
(1) BD is 16.
(2) AE is 9.

For parallelogram ABCD, what is the length of AC?
(1) BD is 16.
(2) AE is 9.
By definition, a parallelogram is a quadrilateral with 2 sets of parallel sides and diagonals that bisect each other.
From statement 1 we cannot determine the length of AC, since ABCD is only defined as a parallelogram and not necessarily a rectangle (which is a special parallelogram with equal diagonals). Therefore, statement 1 alone is not sufficient.
From statement 2, we can determine that  since the definition of a parallelogram states the diagonals bisect each other. Therefore, Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
since the definition of a parallelogram states the diagonals bisect each other. Therefore, Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
By definition, a parallelogram is a quadrilateral with 2 sets of parallel sides and diagonals that bisect each other.
From statement 1 we cannot determine the length of AC, since ABCD is only defined as a parallelogram and not necessarily a rectangle (which is a special parallelogram with equal diagonals). Therefore, statement 1 alone is not sufficient.
From statement 2, we can determine that 
Compare your answer with the correct one above

What is the length of PR?
(1) PQRS is a parallelogram
(2) 

What is the length of PR?
(1) PQRS is a parallelogram
(2)
With the information from statement 1, we don't know the measurements of any parts of PQRS. Therefore, Statement 1 alone is not sufficient.
With the information from statement 2, we know that  , but since we have no confirmed definition of the shape of PQRS, we can't extrapolate the length of SQ to any other length. Therefore, statement 2 alone is not sufficient.
, but since we have no confirmed definition of the shape of PQRS, we can't extrapolate the length of SQ to any other length. Therefore, statement 2 alone is not sufficient.
Even if we look at both statements 1 and 2 together, quadrilateral PQRS looks like a rectangle, but we are only told it is a parallelogram. The figures on the GMAT are not drawn to scale, therefore your eyes cannot be trusted. No difinitive length of PR can be determined. Therefore, statements 1 and 2 together are not sufficient.
Therefore, the correct answer is Statements (1) and (2) TOGETHER are NOT sufficient.
With the information from statement 1, we don't know the measurements of any parts of PQRS. Therefore, Statement 1 alone is not sufficient.
With the information from statement 2, we know that 
Even if we look at both statements 1 and 2 together, quadrilateral PQRS looks like a rectangle, but we are only told it is a parallelogram. The figures on the GMAT are not drawn to scale, therefore your eyes cannot be trusted. No difinitive length of PR can be determined. Therefore, statements 1 and 2 together are not sufficient.
Therefore, the correct answer is Statements (1) and (2) TOGETHER are NOT sufficient.
Compare your answer with the correct one above
Find the length of the diagonal of rectangle DEFT.
I) Side DE is 3 times the length of side TD.
II) The perimeter of the rectangle is  .
.
Find the length of the diagonal of rectangle DEFT.
I) Side DE is 3 times the length of side TD.
II) The perimeter of the rectangle is 
Find the length of the diagonal of rectangle DEFT
I) Side DE is 3 times the length of side TD
II) The perimeter of the rectangle is 
We need to find the diagonal of a rectangle. If we work back from there, we can see that to find the diagonal, we will need to the lengths of both sides of the rectangle.
I) Gives us the relationship between the two sets of sides:

II) Tells us the perimeter, for which we can write and equation:

Now, use the clue from I) to simplify our equation in II) to one variable:




So now that we have our side lengths, use Pythagorean Theorem to find the diagonal:

Find the length of the diagonal of rectangle DEFT
I) Side DE is 3 times the length of side TD
II) The perimeter of the rectangle is
We need to find the diagonal of a rectangle. If we work back from there, we can see that to find the diagonal, we will need to the lengths of both sides of the rectangle.
I) Gives us the relationship between the two sets of sides:
II) Tells us the perimeter, for which we can write and equation:
Now, use the clue from I) to simplify our equation in II) to one variable:
So now that we have our side lengths, use Pythagorean Theorem to find the diagonal:
Compare your answer with the correct one above
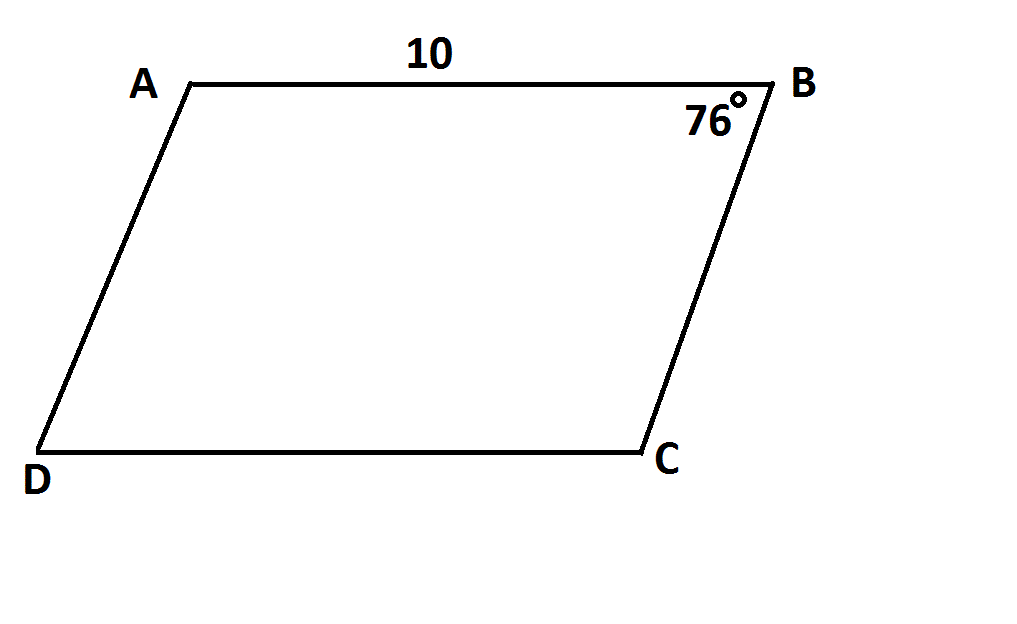
NOTE: Figure NOT drawn to scale.
Is the above figure a parallelogram?
Statement 1: 
Statement 2: 

NOTE: Figure NOT drawn to scale.
Is the above figure a parallelogram?
Statement 1:
Statement 2:
Knowing one pair of sides of a quadrilateral to be congruent is not alone sufficient to prove that figure to be a parallelogram, nor is knowing one pair of sides of a quadrilateral to be parallel. But knowing both about the same pair of sides is sufficient by a theorem of parallelograms.
Knowing one pair of sides of a quadrilateral to be congruent is not alone sufficient to prove that figure to be a parallelogram, nor is knowing one pair of sides of a quadrilateral to be parallel. But knowing both about the same pair of sides is sufficient by a theorem of parallelograms.
Compare your answer with the correct one above