Geometry - GMAT Quantitative Reasoning

Card 0 of 20

Question

Which of the following figures would have exterior angles none of whose degree measures is an integer?

Answer

The sum of the degree measures of any polygon is $360^{\circ }$ . A regular polygon with sides has exterior angles of degree measure $\left (\frac{360}{N} \right )^{\circ }$ . For this to be an integer, 360 must be divisible by .

We can test each of our choices to see which one fails this test.

$360 \div 24 = 15$

$360 \div 30 = 12$

$360 \div 45 = 8$

$360 \div 80 = 4.5$

$360 \div 90 = 4$

Only the eighty-sided regular polygon fails this test, making this the correct choice.

Compare your answer with the correct one above

Question

What is the measure of one exterior angle of a regular twenty-four sided polygon?

Answer

The sum of the measures of the exterior angles of any polygon, one at each vertex, is $360^{\circ }$ . Since a regular polygon with twenty-four sides has twenty-four congruent angles, and therefore, congruent exterior angles, just divide:

$360 \div 24 = 15$

Compare your answer with the correct one above

Question

You are given Pentagon such that:

$m \angle A = \frac{7}{5} m \angle B$

and

$\angle B \cong \angle C \cong \angle D \cong \angle E$

Calculate $m \angle A$

Answer

Let be the common measure of $\angle B$ , $\angle C$ , $\angle D$ , and $\angle E$

Then

$m \angle A = \frac{7}{5} x$

The sum of the measures of the angles of a pentagon is $180 (5 - 2) = 540^{\circ }$ degrees; this translates to the equation

$\frac{7}{5} x + x + x + x + x = 540$

or

$\frac{27}{5} x = 540$

$x = 540 \cdot \frac{5}{27} = 100$

$m \angle A = \frac{7}{5} x = \frac{7}{5} \cdot 100$

$m \angle A = 140$

Compare your answer with the correct one above

Question

The above diagram shows a regular pentagon and a regular hexagon sharing a side. Give $m\angle AVB$ .

Answer

This can more easily be explained if the shared side is extended in one direction, and the new angles labeled.

$\angle1$ and $\angle 2$ are exterior angles of the regular polygons. Also, the measures of the exterior angles of any polygon, one at each vertex, total $360^{\circ }$ . Therefore,

$m \angle1 = \frac{360}{5} = 72^{\circ }$

$m \angle2 = \frac{360}{6} = 60^{\circ }$

Add the measures of the angles to get $m\angle AVB$ :

$m\angle AVB = m\angle 1 + m\angle 2 = 72 + 60 = 132^{\circ }$

Compare your answer with the correct one above

Question

Note: Figure NOT drawn to scale

The figure above shows a square inside a regular pentagon. Give $m\angle 1$ .

Answer

Each angle of a square measures $90^{\circ }$ ; each angle of a regular pentagon measures $180 \cdot3 \div 5 = 108^{\circ }$ . To get $m\angle 1$ , subtract:

$108 - 90 = 18^{\circ }$ .

Compare your answer with the correct one above

Question

Which of the following cannot be the measure of an exterior angle of a regular polygon?

Answer

The sum of the measures of the exterior angles of any polygon, one per vertex, is $360^{\circ }$ . In a regular polygon of sides , then all of these exterior angles are congruent, each measuring $\frac{360^{\circ }}{N}$ .

If is the measure of one of these angles, then $x = \frac{360^{\circ }}{N}$ , or, equivalently, $N = \frac{360^{\circ }}{x}$ . Therefore, for to be a possible measure of an exterior angle, it must divide evenly into 360. We divide each in turn:

$360 \div 6 = 60$

$360 \div 9 = 40$

$360 \div 15 = 24$

$360 \div 16 = 22.5$

Since 16 is the only one of the choices that does not divide evenly into 360, it cannot be the measure of an exterior angle of a regular polygon.

Compare your answer with the correct one above

Question

Note: Figure NOT drawn to scale.

Given:

$\angle A \cong \angle C \cong \angle E$

$\angle B \cong \angle D \cong \angle F$

$m \angle A + 6^{\circ } = m \angle B$

Evaluate $m \angle A$ .

Answer

Call the measure of $\angle A$

$m \angle A = m \angle C = m \angle E = x$

$m \angle A + 6^{\circ } = m \angle B$ , and $\angle B \cong \angle D \cong \angle F$

so

$m \angle B = m \angle D = m \angle F = x + 6$

The sum of the measures of the angles of a hexagon is $180 (6 - 2) = 720 ^{ \circ }$ , so

$m \angle A + m \angle B + m \angle C + m \angle D + m \angle E + m \angle F = 720$

$\ 6x = 702$

$\ x = 702 \div 6 = 117$ , which is the measure of $\angle A$ .

Compare your answer with the correct one above

Question

The above diagram shows a regular pentagon and a regular hexagon sharing a side. What is the measure of $\angle ABC$ ?

Answer

The measure of each interior angle of a regular pentagon is

$\frac{180 (5-2)}{5} = \frac{180 (3)}{5} = 108^{\circ }$

The measure of each interior angle of a regular hexagon is

$\frac{180 (6-2)}{6} = \frac{180 (4)}{6} = 120^{\circ }$

The measure of $\angle ABC$ is the difference of the two, or $12 ^{\circ }$ .

Compare your answer with the correct one above

Question

What is the arithmetic mean of the measures of the angles of a nonagon (a nine-sided polygon)?

Answer

The sum of the measures of the nine angles of any nonagon is calculated as follows:

$180 \cdot \left ( 9-2\right ) =180 \cdot 7= 1,260^{\circ }$

Divide this number by nine to get the arithmetic mean of the measures:

$1,260\div 9 = 140 ^{\circ }$

Compare your answer with the correct one above

Question

What is the median of the measures of the angles of a nonagon (a nine-sided polygon)?

Answer

The sum of the measures of the nine angles of any nonagon is calculated as follows:

$180 \cdot \left ( 9-2\right ) =180 \cdot 7= 1,260^{\circ }$

The median of an odd quantity of numbers is the number that falls in the center position when they are arranged in ascending order; for nine numbers, it will be the fifth-highest number. We now need to show that we need to know the actual numbers in order to find the median.

Case 1: Each angle measures $140 ^{\circ }$ .

The set is $\left { 140,140,140,140,140,140,140,140,140\right }$ and the median is 140.

Case 2: Eight of the angles measure $139 ^{\circ }$ and one of them measures $148 ^{\circ }$ .

The set is $\left {}139, 139, 139, 139, 139, 139, 139, 139, 148 \right }$ and the median is 139.

In both cases, the sum of the angle measures is 1,260, but the medians differ between the two.

Compare your answer with the correct one above

Question

You are given a quadrilateral and a pentagon. What is the mean of the measures of the interior angles of the two polygons?

Answer

The mean of the measures of the four angles of the quadrilateral and the five angles of of the pentagon is their sum divided by 9.

The sum of the measures of the interior angles of any quadrilateral is $180 (4-2) = 360^{\circ }$ . The sum of the measures of the interior angles of any pentagon is $180 (5-2) = 540^{\circ }$ .

The sum of the measures of the interior angles of both polygons is therefore $360 + 540 = 900^{\circ }$ . Divide by 9:

$900 \div 9 = 100^{\circ }$

Compare your answer with the correct one above

Question

Note: Figure NOT drawn to scale.

Given Regular Pentagon . What is $m \angle APN$ ?

Answer

Quadrilateral is a trapezoid, so $m \angle APN + m \angle A = 180 ^{\circ }$ .

$m \angle A = \frac{180 (5-2 )}{5} ^{\circ } = 108 ^{\circ }$ , so

$m \angle APN +108^{\circ } = 180 ^{\circ }$

$m \angle APN +108^{\circ } - 108^{\circ } = 180 ^{\circ } - 108^{\circ }$

$m \angle APN = 72^{\circ }$

Compare your answer with the correct one above

Question

The angles of a pentagon measure $x^{\circ }, \left (x + 10 \right )^{\circ }, \left (x + 10 \right )^{\circ }, \left (x + 15 \right )^{\circ }, \left (x + 25 \right )^{\circ }$ .

Evaluate .

Answer

The sum of the degree measures of the angles of a (five-sided) pentagon is $180 (5 -2 ) ^{\circ } = 540^{\circ }$ , so we can set up and solve the equation:

$x+ \left(x + 10 \right )+ \left (x + 10 \right )+ \left(x + 15 \right )+ \left(x + 25 \right ) = 540$

$5x \div 5 = 480 \div 5$

Compare your answer with the correct one above

Question

The measures of the angles of a pentagon are: $x ^{\circ },\left ( x+23 \right ) {^\circ},\left ( x+23 \right ) {^\circ},\left ( x+33 \right ) {^\circ},\left ( x+41 \right ) {^\circ}$

What is equal to?

Answer

The degree measures of the interior angles of a pentagon total $180 \left ( 5-2\right ) ^{\circ } = 540^{\circ }$ , so

$x + \left ( x+23 \right ) +\left ( x+23 \right ) +\left ( x+33 \right ) +\left ( x+41 \right ) = 540$

$5x \div 5= 420 \div 5$

Compare your answer with the correct one above

Question

What is the measure of an angle in a regular octagon?

Answer

On octagon has sides. The word regular means that all of the angles are equal. Therefore, we can use the general equation for finding the angle measurement of a regular polygon:

$\frac{(n-2)180,\textup{degrees}}{n}$ , where is the number of sides of the polygon.

$\frac{(8-2)180,\textup{degrees}}{8}=135,\textup{degrees}$ .

Compare your answer with the correct one above

Question

Note: Diagram is NOT drawn to scale.

Refer to the above diagram.

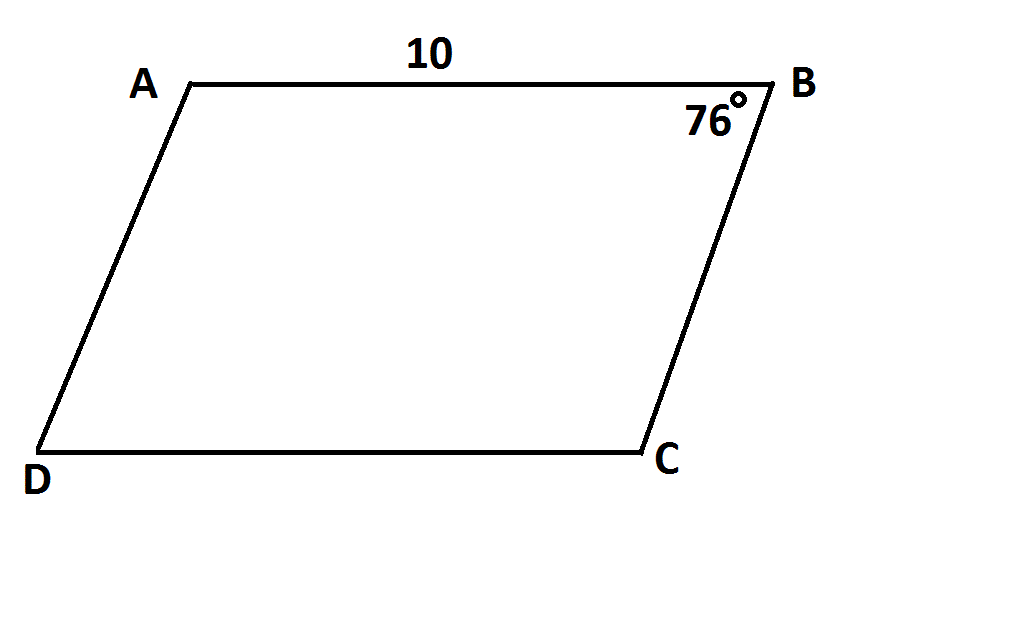
Any of the following facts alone would be enough to prove that $\textrm{Quad} ; ABCD$ is not a parallelogram, EXCEPT:

Answer

Opposite sides of a parallelogram are congruent; if , then , violating this condition.

Consecutive angles of a parallelogram are supplementary; if $m \angle A = 114^{\circ}$ , then $m \angle A + m \angle B= 114 + 76 = 190$ , violating this condition.

Opposite angles of a parallelogram are congruent; if $m \angle D <76^{\circ}$ , then $m \angle D eq m \angle B$ , violating this condition.

Adjacent sides of a parallelogram, however, may or may not be congruent, so the condition that would not by itself prove that the quadrilateral is not a parallelogram.

Compare your answer with the correct one above

Question

Which of the following can not be the measures of the four interior angles of a quadrilateral?

Answer

The four interior angles of a quadrilateral measure a total of $360^{\circ }$ , so we test each group of numbers to see if they have this sum.

This last group does not have the correct sum, so it is the correct choice.

Compare your answer with the correct one above

Question

A circle can be circumscribed about each of the following figures except:

Answer

A circle can be circumscribed about any triangle regardless of its sidelengths or angle measures, so we can eliminate the two triangle choices.

A circle can be circumscribed about a quadrilateral if and only if both pairs of its opposite angles are supplementary. An isosceles trapezoid has this characteristic; this can be proved by the fact that base angles are congruent, and by the Same-Side Interior Angles Statement. For a parallelogram to have this characteristic, since opposite angles are congruent also, all angles must measure $90^{\circ }$ ; the rectangle fits this description, but the rhombus does not.

Compare your answer with the correct one above

Question

Two angles of a parallelogram measure $\left ( x + 70 \right )^{\circ }$ and $\left ( 2x\right +5) ^{\circ }$ . What are the possible values of ?

Answer

Case 1: The two angles are opposite angles of the parallelogram. In this case, they are congruent, and

Case 2: The two angles are consecutive angles of the parallelogram. In this case, they are supplementary, and

$\left ( 2x +5 \right )+\left ( x + 70 \right ) = 180$

$3x \div 3 = 105\div 3$

Compare your answer with the correct one above

Question

Rhombus has two diagonals that intersect at point ; $\angle RHO = 80 ^{\circ }$ .

What is $m \angle RPH$ ?

Answer

The diagonals of a rhombus always intersect at right angles, so $m \angle HPO = 90 ^{\circ }$ . The measures of the interior angles of the rhombus are irrelevant.

Compare your answer with the correct one above

Tap the card to reveal the answer