Calculating arithmetic mean - GMAT Quantitative Reasoning
Card 0 of 20
Consider the following set of numbers:
85, 87, 87, 82, 89
What is the median?
Consider the following set of numbers:
85, 87, 87, 82, 89
What is the median?
Reorder the values in numerical order:82, 85, 87, 87, 89
The median is the center number, 87.
Reorder the values in numerical order:82, 85, 87, 87, 89
The median is the center number, 87.
Compare your answer with the correct one above
Salaries for employees at ABC Company: 1 employee makes $25,000 per year, 4 employees make $40,000 per year, 2 employees make $50,000 per year and 5 employees make $75,000 per year.
What is the average (arithmetic mean) salary for the employees at ABC Company?
Salaries for employees at ABC Company: 1 employee makes $25,000 per year, 4 employees make $40,000 per year, 2 employees make $50,000 per year and 5 employees make $75,000 per year.
What is the average (arithmetic mean) salary for the employees at ABC Company?
The average is found by calculating the total payroll and then dividing by the total number of employees. 

The average is found by calculating the total payroll and then dividing by the total number of employees.
Compare your answer with the correct one above
A bowler had an average (arithmetic mean) score of 215 on the first 5 games she bowled. What must she bowl on the 6th game to average 220 overall?
A bowler had an average (arithmetic mean) score of 215 on the first 5 games she bowled. What must she bowl on the 6th game to average 220 overall?
For the first 5 games the bowler has averaged 215. The equation to calculate the answer is

where  is the score for the sixth game. Next, to solve for the score for the 6th game
is the score for the sixth game. Next, to solve for the score for the 6th game  multiply both sides by 6:
multiply both sides by 6:

which simplifies to:

After subtracting 1,075 from each side we reach the answer:

For the first 5 games the bowler has averaged 215. The equation to calculate the answer is
where 

which simplifies to:
After subtracting 1,075 from each side we reach the answer:
Compare your answer with the correct one above
Ashley averaged a score of 87 on her first 5 tests. She scored a 93 on her 6th test. What is her average test score, assuming all 6 tests are weighted equally?
Ashley averaged a score of 87 on her first 5 tests. She scored a 93 on her 6th test. What is her average test score, assuming all 6 tests are weighted equally?
We can't just average 87 and 93! This will give the wrong answer! The average formula is  .
.
For the first 5 tests,  . Then
. Then  .
.
Now combine that with the 6th test to find the overall average.

We can't just average 87 and 93! This will give the wrong answer! The average formula is 
For the first 5 tests, 

Now combine that with the 6th test to find the overall average.
Compare your answer with the correct one above
Sabrina made $3,000 a month for three months, $4,000 the next month, and $5,200 a month for the following two months. What was her average monthly income for the 6 month period?
Sabrina made $3,000 a month for three months, $4,000 the next month, and $5,200 a month for the following two months. What was her average monthly income for the 6 month period?
Compare your answer with the correct one above
Luke counts the number of gummy bears he eats every day for 1 week: {39, 18, 24, 51, 40, 15, 23}. On average, how many gummy bears does Luke eat each day?
Luke counts the number of gummy bears he eats every day for 1 week: {39, 18, 24, 51, 40, 15, 23}. On average, how many gummy bears does Luke eat each day?
Compare your answer with the correct one above
The average of 10, 25, and 70 is 10 more than the average of 15, 30, and x. What is the missing number?
The average of 10, 25, and 70 is 10 more than the average of 15, 30, and x. What is the missing number?
The average of 10, 25, and 70 is 35: 
So the average of 15, 30, and the unknown number is 25 or, 10 less than the average of 10, 25, and 70 (= 35)
so 



The average of 10, 25, and 70 is 35:
So the average of 15, 30, and the unknown number is 25 or, 10 less than the average of 10, 25, and 70 (= 35)
so
Compare your answer with the correct one above
What is the average of 2_x_, 3_x_ + 2, and 7_x_ +4?
What is the average of 2_x_, 3_x_ + 2, and 7_x_ +4?
Compare your answer with the correct one above
The average high temperature for the week is 85. The first six days of the week have high temperatures of 89, 76, 92, 90, 80, and 84, respectively. What is the high temperature on the seventh day of the week?
The average high temperature for the week is 85. The first six days of the week have high temperatures of 89, 76, 92, 90, 80, and 84, respectively. What is the high temperature on the seventh day of the week?
Compare your answer with the correct one above
Jimmy's grade in his finance class is based on six equally-weighted tests. If Jimmy scored 98, 64, 82, 90, 70, and 88 on the six tests, what was his grade in the class?
Jimmy's grade in his finance class is based on six equally-weighted tests. If Jimmy scored 98, 64, 82, 90, 70, and 88 on the six tests, what was his grade in the class?
Compare your answer with the correct one above

Find the mean of the sample data set.
Find the mean of the sample data set.
The mean of a sample data set is the sum of all of the values divided by the total number of values. In this case:

The mean of a sample data set is the sum of all of the values divided by the total number of values. In this case:
Compare your answer with the correct one above
Sandra's grade in economics depends on seven tests - five hourly tests, a midterm, and a final exam. The midterm counts twice as much as an hourly test; the final, three times as much.
Sandra's grades on the five hourly tests are 84, 86, 76, 89, and 93; her grade on the midterm was 72. What score out of 100 must she achieve on the final exam so that her average score at the end of the term is at least 80?
Sandra's grade in economics depends on seven tests - five hourly tests, a midterm, and a final exam. The midterm counts twice as much as an hourly test; the final, three times as much.
Sandra's grades on the five hourly tests are 84, 86, 76, 89, and 93; her grade on the midterm was 72. What score out of 100 must she achieve on the final exam so that her average score at the end of the term is at least 80?
This is a weighted mean, with the hourly tests assigned a weight of 1, the midterm assigned a weight of 2, and the final assigned a weight of 3. The total of the weights will be
 .
.
If we let  be Sandra's final exam score, Sandra's final weighted average will be
be Sandra's final exam score, Sandra's final weighted average will be



For Sandra to get a final average of 80, then we set the above equal to 80 and calculate  :
:




This is a weighted mean, with the hourly tests assigned a weight of 1, the midterm assigned a weight of 2, and the final assigned a weight of 3. The total of the weights will be

If we let 
For Sandra to get a final average of 80, then we set the above equal to 80 and calculate 
Compare your answer with the correct one above
Consider the following set of numbers:
85, 87, 87, 82, 89
What is the mean?
Consider the following set of numbers:
85, 87, 87, 82, 89
What is the mean?
Compare your answer with the correct one above
The average of the following 6 digits is 75. What is a possible value of  ?
?
80, 78, 78, 70, 71, 
The average of the following 6 digits is 75. What is a possible value of 
80, 78, 78, 70, 71,

Therefore, the sum of all 6 digits must equal 450.


Subtract 377 from both sides.

Therefore, the sum of all 6 digits must equal 450.
Subtract 377 from both sides.
Compare your answer with the correct one above
When assigning a score for the term, a professor takes the mean of all of a student's test scores except for his or her lowest score.
On the first five exams, Donna has achieved the following scores: 76, 84, 80, 65, 91. There is one more exam in the course. Assuming that 100 is the maximum possible score, what is the range of possible final averages she can achieve (nearest tenth, if applicable)?
When assigning a score for the term, a professor takes the mean of all of a student's test scores except for his or her lowest score.
On the first five exams, Donna has achieved the following scores: 76, 84, 80, 65, 91. There is one more exam in the course. Assuming that 100 is the maximum possible score, what is the range of possible final averages she can achieve (nearest tenth, if applicable)?
The worst-case scenario is that she will score 65 or less, in which case her score will be the mean of the scores she has already achieved.

The best-case scenario is that she will score 100, in which case the 65 will be dropped and her score will be the mean of the other five scores.

The worst-case scenario is that she will score 65 or less, in which case her score will be the mean of the scores she has already achieved.
The best-case scenario is that she will score 100, in which case the 65 will be dropped and her score will be the mean of the other five scores.
Compare your answer with the correct one above
If  and
and  , then give the mean of
, then give the mean of  ,
,  ,
,  ,
,  , and
, and  .
.
If 






The mean of  ,
,  ,
,  ,
,  , and
, and  is
is 
If you add both sides of each equation:



or

Equivalently,


 ,
,
making 290 the mean.
The mean of 




If you add both sides of each equation:
or
Equivalently,

making 290 the mean.
Compare your answer with the correct one above
What is the mean of the following data set in terms of  and
and  ?
?

What is the mean of the following data set in terms of 

Add the expressions and divide by the number of terms, 8.
The sum of the expressions is:



Divide this by 8:

Add the expressions and divide by the number of terms, 8.
The sum of the expressions is:
Divide this by 8:
Compare your answer with the correct one above
What is the mean of this data set?

What is the mean of this data set?
Add the numbers and divide by 6:


Add the numbers and divide by 6:
Compare your answer with the correct one above
Julie's grade in a psychology class depends on three tests, each of which are equally weighted; one term paper, which counts half as much as a test; one midterm, which counts for one and one-half as much as a test; and one final, which counts for twice as much as the other tests.
Julie has scored 85%, 84%, and 74% on her three tests, 90% on her term paper, and 72% on her midterm. She is going for an 80% in the course; what is the minimum percent she must score on the final (assuming that 100% is the maximum possible) to achieve this average?
Julie's grade in a psychology class depends on three tests, each of which are equally weighted; one term paper, which counts half as much as a test; one midterm, which counts for one and one-half as much as a test; and one final, which counts for twice as much as the other tests.
Julie has scored 85%, 84%, and 74% on her three tests, 90% on her term paper, and 72% on her midterm. She is going for an 80% in the course; what is the minimum percent she must score on the final (assuming that 100% is the maximum possible) to achieve this average?
Let  be her final grade. Julie's final score is calculated as a weighted mean, so we can set up the following inequality:
be her final grade. Julie's final score is calculated as a weighted mean, so we can set up the following inequality:

Simplify and solve for  :
:








Julie must make a minimum of 82% on the final to meet her goal.
Let 
Simplify and solve for 
Julie must make a minimum of 82% on the final to meet her goal.
Compare your answer with the correct one above
The mean of the following terms is 11. Solve for 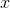 .
.
15, 12, 9, 7, 17, 8, 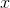
The mean of the following terms is 11. Solve for 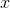
15, 12, 9, 7, 17, 8,
The mean times the number of terms is equal to 77.

The sum of all of the terms must equal 77.



The mean times the number of terms is equal to 77.
The sum of all of the terms must equal 77.
Compare your answer with the correct one above








