Geometry and Graphs - GED Math
Card 0 of 20
What is the measure of each angle of a regular octagon?
What is the measure of each angle of a regular octagon?
The sum of the degree measures of the angles of a polygon with  sides is
sides is  . Since an octagon has eight sides, substitute
. Since an octagon has eight sides, substitute  to get:
to get:

Each angle of a regular polygon has equal measure, so divide this by 8 to get the measure of one angle:
 , the degree measure of one angle.
, the degree measure of one angle.
The sum of the degree measures of the angles of a polygon with 


Each angle of a regular polygon has equal measure, so divide this by 8 to get the measure of one angle:

Compare your answer with the correct one above
Give the number of sides of a regular polygon whose interior angles have measure  .
.
Give the number of sides of a regular polygon whose interior angles have measure 
The easiest way to solve this is to look at the exterior angles, each of which have measure  . Since each exterior angle of a regular polygon with
. Since each exterior angle of a regular polygon with  sides is
sides is  , we solve for
, we solve for  in the following equation:
in the following equation:



The polygon has 36 sides.
The easiest way to solve this is to look at the exterior angles, each of which have measure 



The polygon has 36 sides.
Compare your answer with the correct one above
Give the measure of each interior angle of a regular 72-sided polygon.
Give the measure of each interior angle of a regular 72-sided polygon.
A regular polygon with  sides has interior angles of measure
sides has interior angles of measure  each. Substitute 72 for
each. Substitute 72 for  .
.

A regular polygon with 


Compare your answer with the correct one above

Note: Figure NOT drawn to scale.
The above hexagon is regular. What is  ?
?

Note: Figure NOT drawn to scale.
The above hexagon is regular. What is 
Two of the angles of the quadrilateral formed are angles of a regular hexagon, so each measures
 .
.
The four angles of the quadrilateral are  . Their sum is
. Their sum is  , so we can set up an equation and solve for
, so we can set up an equation and solve for  :
:



Two of the angles of the quadrilateral formed are angles of a regular hexagon, so each measures

The four angles of the quadrilateral are 


Compare your answer with the correct one above

The above octagon is regular. What is  ?
?

The above octagon is regular. What is 
Three of the angles of the pentagon formed are angles of a regular octagon, so each measures
 .
.
The five angles of the pentagon are  . Their sum is
. Their sum is  , so we can set up an equation and solve for
, so we can set up an equation and solve for  :
:



Three of the angles of the pentagon formed are angles of a regular octagon, so each measures

The five angles of the pentagon are 


Compare your answer with the correct one above

Refer to the above diagram.
Which of these is a valid alternative name for  ?
?

Refer to the above diagram.
Which of these is a valid alternative name for 
When naming an angle after three points, the middle letter must be its vertex, or the point at which its sides meet - this is  . The other two letters must refer to points on its two sides. Therefore,
. The other two letters must refer to points on its two sides. Therefore,  includes
includes  on one side, making one of its sides
on one side, making one of its sides  , and
, and  on the other, making the other side
on the other, making the other side  .
.
An alternative name for this angle must be one of two things:
It can be named only after its vertex - that is,  - but only if there is no ambiguity as to which angle is being named. Since more than one angle in the diagram has vertex
- but only if there is no ambiguity as to which angle is being named. Since more than one angle in the diagram has vertex  ,
,  is not a correct choice.
is not a correct choice.
It can be named after three points. Again, the middle letter must be vertex  , so we can throw out
, so we can throw out  and
and  .
.
The only possible choice is  .
.
When naming an angle after three points, the middle letter must be its vertex, or the point at which its sides meet - this is 





An alternative name for this angle must be one of two things:
It can be named only after its vertex - that is, 


It can be named after three points. Again, the middle letter must be vertex 


The only possible choice is 
Compare your answer with the correct one above

Refer to the above figure.  is equilateral, and Quadrilateral
is equilateral, and Quadrilateral  is a square.
is a square.
Evaluate  .
.

Refer to the above figure. 

Evaluate 
By angle addition,
 .
.
 , as an angle of an equilateral triangle, has measure
, as an angle of an equilateral triangle, has measure  .
.
 , as an angle of a square, has measure
, as an angle of a square, has measure  .
.
Therefore,
 .
.
By angle addition,





Therefore,

Compare your answer with the correct one above

Refer to the above figure, which shows Square  and regular Pentagon
and regular Pentagon  .
.
Evaluate  .
.

Refer to the above figure, which shows Square 

Evaluate 
By angle addition,
 .
.
 is an angle of a regular pentagon and has measure
is an angle of a regular pentagon and has measure  .
.
 is one of two acute angles of isosceles right triangle
is one of two acute angles of isosceles right triangle  , so
, so  .
.

By angle addition,






Compare your answer with the correct one above

Note: Figure NOT drawn to scale.
Refer to the above figure.  is equilateral and Pentagon
is equilateral and Pentagon  is regular.
is regular.
Evaluate  .
.

Note: Figure NOT drawn to scale.
Refer to the above figure. 

Evaluate 
First, we find  .
.
By angle addition,
 .
.
 is an angle of a regular pentagon and has measure
is an angle of a regular pentagon and has measure  .
.
 , as an angle of an equilateral triangle, has measure
, as an angle of an equilateral triangle, has measure  .
.


 is equilateral, so
is equilateral, so  ; Pentagon
; Pentagon  is regular, so
is regular, so  . Therefore,
. Therefore,  , and by the Isosceles Triangle Theorem,
, and by the Isosceles Triangle Theorem,  .
.
The degree measures of three angles of a triangle total  , so:
, so:





First, we find 
By angle addition,











The degree measures of three angles of a triangle total 
Compare your answer with the correct one above
Three consecutive even angles add up to  . What must be the value of the second largest angle?
. What must be the value of the second largest angle?
Three consecutive even angles add up to 
Let  be an even angle. The next consecutive even values are
be an even angle. The next consecutive even values are  .
.
Set up an equation such that all angles added equal to 180.



Divide by three on both sides.


The second largest angle is  .
.
Substitute the value of  in to the expression.
in to the expression.

The answer is: 
Let 

Set up an equation such that all angles added equal to 180.
Divide by three on both sides.
The second largest angle is 
Substitute the value of 
The answer is:
Compare your answer with the correct one above
In Rhombus 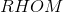 ,
,  . If
. If  is constructed, which of the following is true about
is constructed, which of the following is true about  ?
?
In Rhombus 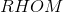



The figure referenced is below.

The sides of a rhombus are congruent by definition, so  , making
, making  isosceles (and possibly equilateral).
isosceles (and possibly equilateral).
Also, consecutive angles of a rhombus are supplementary, as they are with all parallelograms, so
 .
.
 , having measure greater than
, having measure greater than  , is obtuse, making
, is obtuse, making  an obtuse triangle. Also, the triangle is not equilateral, since such a triangle must have three
an obtuse triangle. Also, the triangle is not equilateral, since such a triangle must have three  angles.
angles.
The correct response is that  is obtuse and isosceles, but not equilateral.
is obtuse and isosceles, but not equilateral.
The figure referenced is below.

The sides of a rhombus are congruent by definition, so 

Also, consecutive angles of a rhombus are supplementary, as they are with all parallelograms, so





The correct response is that 
Compare your answer with the correct one above
Given Quadrilateral  , which of these statements would prove that it is a parallelogram?
, which of these statements would prove that it is a parallelogram?
I)  and
and 
II)  and
and 
III)  and
and  are supplementary and
are supplementary and  and
and  are supplementary
are supplementary
Given Quadrilateral 
I) 
II) 
III) 



Statement I asserts that two pairs of consecutive angles are congruent. This does not prove that the figure is a parallelogram. For example, an isosceles trapezoid has two pairs of congruent base angles, which are consecutive.
Statement II asserts that both pairs of opposite angles are congruent. By a theorem of geometry, this proves the quadrilateral to be a parallelogram.
Statement III asserts that two pairs of consecutive angles are supplementary. While all parallelograms have this characteristic, trapezoids do as well, so this does not prove the figure a parallelogram.
The correct response is Statement II only.
Statement I asserts that two pairs of consecutive angles are congruent. This does not prove that the figure is a parallelogram. For example, an isosceles trapezoid has two pairs of congruent base angles, which are consecutive.
Statement II asserts that both pairs of opposite angles are congruent. By a theorem of geometry, this proves the quadrilateral to be a parallelogram.
Statement III asserts that two pairs of consecutive angles are supplementary. While all parallelograms have this characteristic, trapezoids do as well, so this does not prove the figure a parallelogram.
The correct response is Statement II only.
Compare your answer with the correct one above
You are given Parallelogram  with
with  . Which of the following statements, along with what you are given, would be enough to prove that Parallelogram
. Which of the following statements, along with what you are given, would be enough to prove that Parallelogram  is a rectangle?
is a rectangle?
I) 
II) 
III) 
You are given Parallelogram 


I)
II)
III)
A rectangle is defined as a parallelogram with four right, or  , angles.
, angles.
Since opposite angles of a paralellogram are congruent, if one angle measures  , so does its opposite. Since consecutive angles of a paralellogram are supplementary - that is, their degree measures total
, so does its opposite. Since consecutive angles of a paralellogram are supplementary - that is, their degree measures total  - if one angle measures
- if one angle measures  , then both of the neighboring angles measure
, then both of the neighboring angles measure  .
.
In short, in a parallelogram, if one angle is right, all are right and the parallelogram is a rectangle. All three statements assert that one angle is right, so from any one, it follows that the figure is a rectangle. The correct response is Statements I, II, or III.
Note that the sidelengths are irrelevant.
A rectangle is defined as a parallelogram with four right, or 
Since opposite angles of a paralellogram are congruent, if one angle measures 



In short, in a parallelogram, if one angle is right, all are right and the parallelogram is a rectangle. All three statements assert that one angle is right, so from any one, it follows that the figure is a rectangle. The correct response is Statements I, II, or III.
Note that the sidelengths are irrelevant.
Compare your answer with the correct one above
If the rectangle has a width of 5 and a length of 10, what is the area of the rectangle?
If the rectangle has a width of 5 and a length of 10, what is the area of the rectangle?
Write the area for a rectangle.

Substitute the given dimensions.

The answer is: 
Write the area for a rectangle.
Substitute the given dimensions.
The answer is:
Compare your answer with the correct one above
In the figure below, find the measure of the largest angle.

In the figure below, find the measure of the largest angle.

Recall that in a quadrilateral, the interior angles must add up to  .
.
Thus, we can solve for  :
:




Now, to find the largest angle, plug in the value of  into each expression for each angle.
into each expression for each angle.




The largest angle is  .
.
Recall that in a quadrilateral, the interior angles must add up to 
Thus, we can solve for 
Now, to find the largest angle, plug in the value of 
The largest angle is 
Compare your answer with the correct one above
Which of the following can be the measures of the three angles of an acute isosceles triangle?
Which of the following can be the measures of the three angles of an acute isosceles triangle?
For the triangle to be acute, all three angles must measure less than  . We can eliminate
. We can eliminate  and
and  for this reason.
for this reason.
In an isosceles triangle, at least two angles are congruent, so we can eliminate  .
.
The degree measures of the three angles of a triangle must total 180, so, since  , we can eliminate
, we can eliminate  .
.
 is correct.
is correct.
For the triangle to be acute, all three angles must measure less than 


In an isosceles triangle, at least two angles are congruent, so we can eliminate 
The degree measures of the three angles of a triangle must total 180, so, since 


Compare your answer with the correct one above
Which of the following describes a triangle with sides of length 9 feet, 3 yards, and 90 inches?
Which of the following describes a triangle with sides of length 9 feet, 3 yards, and 90 inches?
One yard is equal to three feet, and one foot is equal to twelve inches. Therefore, 9 feet is equal to  inches, and 3 yards is equal to
inches, and 3 yards is equal to  inches. The triangle has sides of measure 90 inches, 108 inches, and 108 inches. Exactly two sides are of equal measure, so it is isosceles but not equilateral.
inches. The triangle has sides of measure 90 inches, 108 inches, and 108 inches. Exactly two sides are of equal measure, so it is isosceles but not equilateral.
One yard is equal to three feet, and one foot is equal to twelve inches. Therefore, 9 feet is equal to 

Compare your answer with the correct one above

Note: Figure NOT drawn to scale.
Refer to the above triangle. Evaluate  .
.

Note: Figure NOT drawn to scale.
Refer to the above triangle. Evaluate 
The degree measures of a triangle total  , so
, so






The degree measures of a triangle total 
Compare your answer with the correct one above

Note: Figure NOT drawn to scale.
Refer to the above figure. Evaluate  .
.

Note: Figure NOT drawn to scale.
Refer to the above figure. Evaluate 
The degree measures of the interior angles of a triangle total  , so, if we let
, so, if we let  be the measure of the unmarked angle, then
be the measure of the unmarked angle, then



Three angles with measures  together form a straight angle, so
together form a straight angle, so






The degree measures of the interior angles of a triangle total 

Three angles with measures 
Compare your answer with the correct one above

Figure drawn to scale.
Refer to the above diagram.
Which of the following is a valid description of  ?
?

Figure drawn to scale.
Refer to the above diagram.
Which of the following is a valid description of 
One of the angles of  - namely,
- namely,  - can be seen to be an obtuse angle, as it is wider than a right angle. This makes
- can be seen to be an obtuse angle, as it is wider than a right angle. This makes  , by definition, an obtuse triangle.
, by definition, an obtuse triangle.
One of the angles of 


Compare your answer with the correct one above