Squares, Rectangles, and Parallelograms - GED Math
Card 0 of 20
In Rhombus 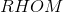 ,
,  . If
. If  is constructed, which of the following is true about
is constructed, which of the following is true about  ?
?
In Rhombus 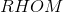



The figure referenced is below.

The sides of a rhombus are congruent by definition, so  , making
, making  isosceles (and possibly equilateral).
isosceles (and possibly equilateral).
Also, consecutive angles of a rhombus are supplementary, as they are with all parallelograms, so
 .
.
 , having measure greater than
, having measure greater than  , is obtuse, making
, is obtuse, making  an obtuse triangle. Also, the triangle is not equilateral, since such a triangle must have three
an obtuse triangle. Also, the triangle is not equilateral, since such a triangle must have three  angles.
angles.
The correct response is that  is obtuse and isosceles, but not equilateral.
is obtuse and isosceles, but not equilateral.
The figure referenced is below.

The sides of a rhombus are congruent by definition, so 

Also, consecutive angles of a rhombus are supplementary, as they are with all parallelograms, so





The correct response is that 
Compare your answer with the correct one above
Given Quadrilateral  , which of these statements would prove that it is a parallelogram?
, which of these statements would prove that it is a parallelogram?
I)  and
and 
II)  and
and 
III)  and
and  are supplementary and
are supplementary and  and
and  are supplementary
are supplementary
Given Quadrilateral 
I) 
II) 
III) 



Statement I asserts that two pairs of consecutive angles are congruent. This does not prove that the figure is a parallelogram. For example, an isosceles trapezoid has two pairs of congruent base angles, which are consecutive.
Statement II asserts that both pairs of opposite angles are congruent. By a theorem of geometry, this proves the quadrilateral to be a parallelogram.
Statement III asserts that two pairs of consecutive angles are supplementary. While all parallelograms have this characteristic, trapezoids do as well, so this does not prove the figure a parallelogram.
The correct response is Statement II only.
Statement I asserts that two pairs of consecutive angles are congruent. This does not prove that the figure is a parallelogram. For example, an isosceles trapezoid has two pairs of congruent base angles, which are consecutive.
Statement II asserts that both pairs of opposite angles are congruent. By a theorem of geometry, this proves the quadrilateral to be a parallelogram.
Statement III asserts that two pairs of consecutive angles are supplementary. While all parallelograms have this characteristic, trapezoids do as well, so this does not prove the figure a parallelogram.
The correct response is Statement II only.
Compare your answer with the correct one above
You are given Parallelogram  with
with  . Which of the following statements, along with what you are given, would be enough to prove that Parallelogram
. Which of the following statements, along with what you are given, would be enough to prove that Parallelogram  is a rectangle?
is a rectangle?
I) 
II) 
III) 
You are given Parallelogram 


I)
II)
III)
A rectangle is defined as a parallelogram with four right, or  , angles.
, angles.
Since opposite angles of a paralellogram are congruent, if one angle measures  , so does its opposite. Since consecutive angles of a paralellogram are supplementary - that is, their degree measures total
, so does its opposite. Since consecutive angles of a paralellogram are supplementary - that is, their degree measures total  - if one angle measures
- if one angle measures  , then both of the neighboring angles measure
, then both of the neighboring angles measure  .
.
In short, in a parallelogram, if one angle is right, all are right and the parallelogram is a rectangle. All three statements assert that one angle is right, so from any one, it follows that the figure is a rectangle. The correct response is Statements I, II, or III.
Note that the sidelengths are irrelevant.
A rectangle is defined as a parallelogram with four right, or 
Since opposite angles of a paralellogram are congruent, if one angle measures 



In short, in a parallelogram, if one angle is right, all are right and the parallelogram is a rectangle. All three statements assert that one angle is right, so from any one, it follows that the figure is a rectangle. The correct response is Statements I, II, or III.
Note that the sidelengths are irrelevant.
Compare your answer with the correct one above
If the rectangle has a width of 5 and a length of 10, what is the area of the rectangle?
If the rectangle has a width of 5 and a length of 10, what is the area of the rectangle?
Write the area for a rectangle.

Substitute the given dimensions.

The answer is: 
Write the area for a rectangle.
Substitute the given dimensions.
The answer is:
Compare your answer with the correct one above
In the figure below, find the measure of the largest angle.

In the figure below, find the measure of the largest angle.

Recall that in a quadrilateral, the interior angles must add up to  .
.
Thus, we can solve for  :
:




Now, to find the largest angle, plug in the value of  into each expression for each angle.
into each expression for each angle.




The largest angle is  .
.
Recall that in a quadrilateral, the interior angles must add up to 
Thus, we can solve for 
Now, to find the largest angle, plug in the value of 
The largest angle is 
Compare your answer with the correct one above
Find the area of the trapezoid:

Find the area of the trapezoid:

The area of a trapezoid is calculated using the following equation:

The area of a trapezoid is calculated using the following equation:
Compare your answer with the correct one above
A rectangle has length 10 inches and width 5 inches. Each dimension is increased by 3 inches. By what percent has the area of the rectangle increased?
A rectangle has length 10 inches and width 5 inches. Each dimension is increased by 3 inches. By what percent has the area of the rectangle increased?
The area of a rectangle is its length times its width.
Its original area is  square inches; its new area is
square inches; its new area is  square inches. The area has increased by
square inches. The area has increased by
 .
.
The area of a rectangle is its length times its width.
Its original area is 


Compare your answer with the correct one above
A rectangle has length 10 inches and width 8 inches. Its length is increased by 2 inches, and its width is decreased by 2 inches. By what percent has the area of the rectangle decreased?
A rectangle has length 10 inches and width 8 inches. Its length is increased by 2 inches, and its width is decreased by 2 inches. By what percent has the area of the rectangle decreased?
The area of a rectangle is its length times its width.
Its original area is  square inches; its new area is
square inches; its new area is  square inches. The area has decreased by
square inches. The area has decreased by
 .
.
The area of a rectangle is its length times its width.
Its original area is 


Compare your answer with the correct one above
The length of each side of a square is increased by 10%. By what percent has its area increased?
The length of each side of a square is increased by 10%. By what percent has its area increased?
Let  be the original sidelength of the square. Increasing this by 10% is the same as adding 0.1 times that sidelength to the original sidelength. The new sidelength is therefore
be the original sidelength of the square. Increasing this by 10% is the same as adding 0.1 times that sidelength to the original sidelength. The new sidelength is therefore

The area of a square is the square of its sidelength.
The area of the square was originally  ; it is now
; it is now

That is, the area has increased by
 .
.
Let 
The area of a square is the square of its sidelength.
The area of the square was originally 
That is, the area has increased by

Compare your answer with the correct one above

The above figure depicts the rectangular swimming pool at an apartment. The apartment manager needs to purchase a tarp that will cover this pool completely. However, because of the cutting device the pool store uses, the length and the width of the tarp must each be a multiple of four yards. Also, the tarp must be at least one yard longer and one yard wider than the pool.
What will be the minimum area of the tarp the manager purchases?

The above figure depicts the rectangular swimming pool at an apartment. The apartment manager needs to purchase a tarp that will cover this pool completely. However, because of the cutting device the pool store uses, the length and the width of the tarp must each be a multiple of four yards. Also, the tarp must be at least one yard longer and one yard wider than the pool.
What will be the minimum area of the tarp the manager purchases?
Three feet make a yard, so the length and width of the pool are  yards and
yards and  yards, respectively. Since the dimensions of the tarp must exceed those of the pool by at least one yard, the tarp must be at least
yards, respectively. Since the dimensions of the tarp must exceed those of the pool by at least one yard, the tarp must be at least  yards by
yards by  yards; but since both dimensions must be multiples of four yards, we take the next multiple of four for each.
yards; but since both dimensions must be multiples of four yards, we take the next multiple of four for each.
The tarp must be 20 yards by 16 yards, so the area of the tarp is the product of these dimensions, or
 square yards.
square yards.
Three feet make a yard, so the length and width of the pool are 



The tarp must be 20 yards by 16 yards, so the area of the tarp is the product of these dimensions, or

Compare your answer with the correct one above

Note: Figure NOT drawn to scale
Refer to the above figure, which shows a rectangular garden (in green) surrounded by a dirt path five feet wide throughout. What is the area of that dirt path?

Note: Figure NOT drawn to scale
Refer to the above figure, which shows a rectangular garden (in green) surrounded by a dirt path five feet wide throughout. What is the area of that dirt path?
The dirt path can be seen as the region between two rectangles. The outer rectangle has length and width 100 feet and 60 feet, respectively, so its area is
 square feet.
square feet.
The inner rectangle has length and width  feet and
feet and  feet, respectively, so its area is
feet, respectively, so its area is
 square feet.
square feet.
The area of the path is the difference of the two:
 square feet.
square feet.
The dirt path can be seen as the region between two rectangles. The outer rectangle has length and width 100 feet and 60 feet, respectively, so its area is

The inner rectangle has length and width 


The area of the path is the difference of the two:

Compare your answer with the correct one above

Note: Figure NOT drawn to scale
Refer to the above figure, which shows a rectangular garden (in green) surrounded by a dirt path (in brown). The dirt path is  feet wide throughout. Which of the following polynomials gives the area of the garden?
feet wide throughout. Which of the following polynomials gives the area of the garden?

Note: Figure NOT drawn to scale
Refer to the above figure, which shows a rectangular garden (in green) surrounded by a dirt path (in brown). The dirt path is 
The length of the garden is  feet less than that of the entire lot, or
feet less than that of the entire lot, or
 .
.
The width of the garden is  feet less than that of the entire lot, or
feet less than that of the entire lot, or
 .
.
The area of the garden is their product:




The length of the garden is 

The width of the garden is 

The area of the garden is their product:
Compare your answer with the correct one above

Note: Figure NOT drawn to scale.
Refer to the above figure, which shows a rectangular garden (in green) surrounded by a dirt path (in brown). The dirt path is five feet wide throughout. Which of the following polynomials gives the area of the garden in square feet?

Note: Figure NOT drawn to scale.
Refer to the above figure, which shows a rectangular garden (in green) surrounded by a dirt path (in brown). The dirt path is five feet wide throughout. Which of the following polynomials gives the area of the garden in square feet?
The length of the garden is  feet less than that of the entire lot, or
feet less than that of the entire lot, or
 .
.
The width of the garden is  less than that of the entire lot, or
less than that of the entire lot, or
 .
.
The area of the garden is their product:




The length of the garden is 

The width of the garden is 

The area of the garden is their product:
Compare your answer with the correct one above

Note: Figure NOT drawn to scale
Refer to the above diagram.
Half of Rectangle  is pink.
is pink.  .
.
Evaluate  .
.

Note: Figure NOT drawn to scale
Refer to the above diagram.
Half of Rectangle 

Evaluate 
Rectangle  has length
has length  and width
and width  , so it has area
, so it has area
 .
.
The area of Rectangle  is twice that of Rectangle
is twice that of Rectangle  , or 600. Its length is
, or 600. Its length is
 .
.
Its width is
 .
.
Plug in what we know and solve for  :
:




Rectangle 



The area of Rectangle 


Its width is

Plug in what we know and solve for 
Compare your answer with the correct one above

Note: Figure NOT drawn to scale

What percent of Rectangle  is pink?
is pink?

Note: Figure NOT drawn to scale
What percent of Rectangle 
The pink region is Rectangle  . Its length and width are
. Its length and width are


so its area is the product of these, or
 .
.
The length and width of Rectangle  are
are


so its area is the product of these, or
 .
.
So we want to know what percent 112 is of 240, which can be answered as follows:

The pink region is Rectangle 
so its area is the product of these, or

The length and width of Rectangle 
so its area is the product of these, or

So we want to know what percent 112 is of 240, which can be answered as follows:
Compare your answer with the correct one above

Note: Figure NOT drawn to scale

What percent of Rectangle  is white?
is white?

Note: Figure NOT drawn to scale
What percent of Rectangle 
The pink region is Rectangle  . Its length and width are
. Its length and width are


so its area is the product of these, or
 .
.
The length and width of Rectangle  are
are


so its area is the product of these, or
 .
.
The white region is Rectangle  cut from Rectangle
cut from Rectangle  , so its area is the difference of the two:
, so its area is the difference of the two:
 .
.
So we want to know what percent 102 is of 200, which can be answered as follows:

The pink region is Rectangle 
so its area is the product of these, or

The length and width of Rectangle 
so its area is the product of these, or

The white region is Rectangle 


So we want to know what percent 102 is of 200, which can be answered as follows:
Compare your answer with the correct one above

Note: Figure NOT drawn to scale.
Calculate the area of Rhombus  in the above diagram if:
in the above diagram if:



Note: Figure NOT drawn to scale.
Calculate the area of Rhombus 
The area of a rhombus is half the product of the lengths of diagonals  and
and  . This is
. This is
 .
.
The area of a rhombus is half the product of the lengths of diagonals 


Compare your answer with the correct one above
Find the area of a square with a side of  .
.
Find the area of a square with a side of 
Write the formula for the area of a square.

Substitute the side into the equation.

Simplify the equation.
The answer is: 
Write the formula for the area of a square.
Substitute the side into the equation.
Simplify the equation.
The answer is:
Compare your answer with the correct one above
If a rectangle has a length of 18cm and a width that is half the length, what is the area of the rectangle?
If a rectangle has a length of 18cm and a width that is half the length, what is the area of the rectangle?
To find the area of a rectangle, we will use the following formula:

where l is the length and w is the width of the rectangle.
Now, we know the length of the rectangle is 18cm. We also know the width is half the length. Therefore, the width is 9cm. So, we can substitute. We get


To find the area of a rectangle, we will use the following formula:
where l is the length and w is the width of the rectangle.
Now, we know the length of the rectangle is 18cm. We also know the width is half the length. Therefore, the width is 9cm. So, we can substitute. We get
Compare your answer with the correct one above
If a square has a length of 10in, find the area.
If a square has a length of 10in, find the area.
To find the area of a square, we will use the following formula:

where l is the length and w is the width of the square.
Now, we know the length of the square is 10in. Because it is a square, all sides are equal. Therefore, the length is also 10in. So, we can substitute. We get


To find the area of a square, we will use the following formula:
where l is the length and w is the width of the square.
Now, we know the length of the square is 10in. Because it is a square, all sides are equal. Therefore, the length is also 10in. So, we can substitute. We get
Compare your answer with the correct one above