Nonhomogeneous Linear Systems - Differential Equations
Card 0 of 1
Solve the following system. 
Solve the following system.
First, we will need the complementary solution, and a fundamental matrix for the homogeneous system. Thus, we find the characteristic equation of the matrix given.
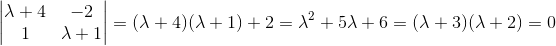
Using  , we then find the eigenvectors by solving for the eigenspace.
, we then find the eigenvectors by solving for the eigenspace.


This has solutions  , or
, or  . So a suitable eigenvector is simply
. So a suitable eigenvector is simply  .
.
Repeating for  ,
,

This has solutions 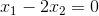 , and thus a suitable eigenvector is
, and thus a suitable eigenvector is  . Thus, our complementary solution is
. Thus, our complementary solution is  and our fundamental matrix (though in this case, not the matrix exponential) is
and our fundamental matrix (though in this case, not the matrix exponential) is  . Variation of parameters tells us that the particular solution is given by
. Variation of parameters tells us that the particular solution is given by 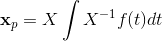 , so first we find
, so first we find  using the inverse rule for 2x2 matrices. Thus,
using the inverse rule for 2x2 matrices. Thus,  . Plugging in, we have
. Plugging in, we have  . So
. So 
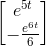 .
.
Finishing up, we have  .
.
Adding the particular solution to the homogeneous, we get a final general solution of 
First, we will need the complementary solution, and a fundamental matrix for the homogeneous system. Thus, we find the characteristic equation of the matrix given.
Using 
This has solutions 


Repeating for 
This has solutions 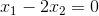



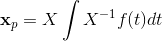




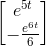
Finishing up, we have 
Adding the particular solution to the homogeneous, we get a final general solution of
Compare your answer with the correct one above