Prove Geometric Theorems: Lines and Angles - Common Core: High School - Geometry
Card 0 of 20
Which of the following describes 
and 
?
Which of the following describes 
To answer this question, we must understand the definition of vertically opposite angles. Vertically opposite angles are angles that are formed opposite of each other when two lines intersect. Vertically opposite angles are always congruent to each other.
To answer this question, we must understand the definition of vertically opposite angles. Vertically opposite angles are angles that are formed opposite of each other when two lines intersect. Vertically opposite angles are always congruent to each other.
Compare your answer with the correct one above
Which of the following describes 
and 
?
Which of the following describes 
To answer this question, we must understand the definition of alternate exterior angles. When a transversal line intersects two parallel lines, 4 exterior angles are formed. Alternate exterior angles are angles on the outsides of these two parallel lines and opposite of each other.
To answer this question, we must understand the definition of alternate exterior angles. When a transversal line intersects two parallel lines, 4 exterior angles are formed. Alternate exterior angles are angles on the outsides of these two parallel lines and opposite of each other.
Compare your answer with the correct one above
True or False: Lines AB and CD are parallel.
True or False: Lines AB and CD are parallel.
We know that lines AB and CD are parallel due to the information we get from the angles formed by the transversal line. There are:
- two pairs of congruent vertically opposite angles
- two pairs of congruent alternate interior angles
- two pairs of congruent alternate exterior angles
- two pairs of congruent corresponding angles
Just using any one of these facts is enough proof that lines AB and CD are parallel.
We know that lines AB and CD are parallel due to the information we get from the angles formed by the transversal line. There are:
- two pairs of congruent vertically opposite angles
- two pairs of congruent alternate interior angles
- two pairs of congruent alternate exterior angles
- two pairs of congruent corresponding angles
Just using any one of these facts is enough proof that lines AB and CD are parallel.
Compare your answer with the correct one above
What does it mean for two angles to be complementary angles?
What does it mean for two angles to be complementary angles?
The definition of complementary angles is: any two angles that sum to 90. We most often see these angles as the two angles in a right triangle that are not the right angle. These two angles do not have to only be in right triangles, however. Complementary triangles are any pair of angles that add up to be 90.
The definition of complementary angles is: any two angles that sum to 90. We most often see these angles as the two angles in a right triangle that are not the right angle. These two angles do not have to only be in right triangles, however. Complementary triangles are any pair of angles that add up to be 90.
Compare your answer with the correct one above
Lines 
and 
are parallel. Using this information, find the values for angles 
, and 
.
Lines 
We must use the fact that lines 
and 
are parallel lines to solve for the missing angles. We will break it down to solve for each angle one at a time.
Angle 
:
We know that angle 
’s supplementary angle. Supplementary angles are two angles that add up to 180 degrees. These two are supplementary angles because they form a straight line and straight lines are always 180 degrees. So to solve for angle 
we simply subtract it’s supplementary angle from 180.
Angle 
:
We now know that angle 
is 130 degrees. We can either use that fact that angles 
and 
are opposite vertical angles to find the value of angle 
or we can use that fact that angle 
’s supplementary angle is the given angle of 50 degrees. If we use the latter, we would use the same procedure as last time to solve for angle 
. If we use the fact that angles 
and 
are opposite vertical angles, we know that they are congruent. Since angle 
then angle 
.
Angle 
:
To find angle 
we can use the fact that angles 
and 
are corresponding angles and therefore are congruent or we can use the fact that angles 
and 
are alternate interior angles and therefore are congruent. Either method that we use will show that 
.
Angle 
:
To find angle 
we can use that fact that the given angle of 50 degrees and angle 
are alternate exterior angles and therefore are congruent, or we can use the fact that angle 
is angle 
's supplementary angle. We know that the given angle and angle 
are alternate exterior angles so 
.
We must use the fact that lines 
Angle 
We know that angle
Angle 
We now know that angle 
Angle 
To find angle 
Angle 
To find angle 
Compare your answer with the correct one above
True or False: The following figure shows a line segment.
True or False: The following figure shows a line segment.
The figure shows a ray. A ray has a single endpoint and the other end extends infinitely. This is represented by an arrowhead on the end that extends infinitely.
The figure shows a ray. A ray has a single endpoint and the other end extends infinitely. This is represented by an arrowhead on the end that extends infinitely.
Compare your answer with the correct one above
Solve for 
?
Solve for 
and the given angle are supplementary angles. This means that they sum up to 180 degrees.
So
So
Compare your answer with the correct one above
Are lines 
and 
parallel?
Are lines 
The angles formed by the transversal line intersecting lines 
and 
does not form congruent opposite vertical angles. Therefore these two lines are not congruent.
The angles formed by the transversal line intersecting lines 
Compare your answer with the correct one above
What are the values of angles 
and 
?
What are the values of angles 
We are able to use the relationship of opposite vertical angles to solve this problem. The given angle and angle 
are opposite vertical angles and therefore must be congruent. So 
. 
is supplementary to both angles 
and 
so they must be congruent. 
and 
are also opposite vertical angles so they must be congruent in that respect as well. So
We are able to use the relationship of opposite vertical angles to solve this problem. The given angle and angle 
Compare your answer with the correct one above
Solve for angle 1.
Solve for angle 1.
Even though it may not be obvious at first, the given angle is actually a supplementary angle to angle 
. This is because the given angle is corresponding (and therefore congruent) angles to the angle adjacent to angle 
. Since they are supplementary we can set up the following equation.
Even though it may not be obvious at first, the given angle is actually a supplementary angle to angle 
Compare your answer with the correct one above
True or False: The Vertical Angle Theorem states that if two angles are vertical angles, then they have equal measure.
True or False: The Vertical Angle Theorem states that if two angles are vertical angles, then they have equal measure.
This is a true statement. If two lines are intersecting, then their vertical angles are congruent. Vertical angles are the opposite angles formed when two lines intersect. The figure below shows an example of this.
This is a true statement. If two lines are intersecting, then their vertical angles are congruent. Vertical angles are the opposite angles formed when two lines intersect. The figure below shows an example of this.
Compare your answer with the correct one above
Which of the following is the Same Side Interior Angles Theorem?
Which of the following is the Same Side Interior Angles Theorem?
Consider the figure below. If a transversal line intersects two parallel lines, then the two interior angles on the same side of the transversal (the two consecutive, interior angles of the transversal) are supplementary. This means that they add up to be 180.
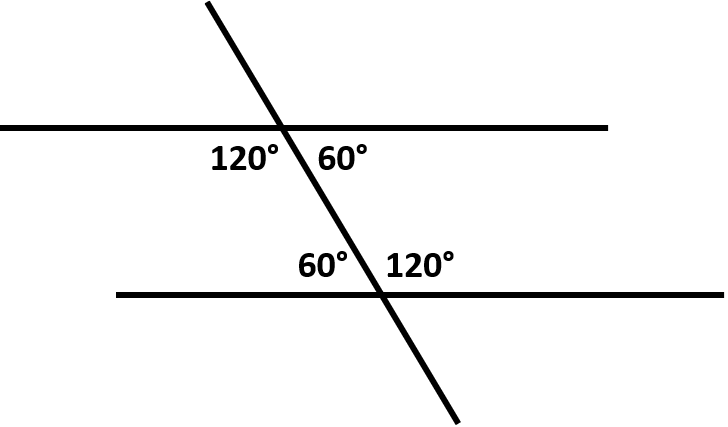
Consider the figure below. If a transversal line intersects two parallel lines, then the two interior angles on the same side of the transversal (the two consecutive, interior angles of the transversal) are supplementary. This means that they add up to be 180.
Compare your answer with the correct one above
Prove that if the following lines 
and 
are parallel, then their alternate interior angles are equal.
Prove that if the following lines 
Follow the detailed proof below.
Follow the detailed proof below.
Compare your answer with the correct one above
Prove that if the following lines 
and 
are parallel, then the interior angles on the same side of the transversal are supplementary.
Prove that if the following lines 
Follow the detailed proof below.
Follow the detailed proof below.
Compare your answer with the correct one above
Prove that if 
, then lines 
and 
are parallel.
Prove that if 
Follow the detailed proof below.
Follow the detailed proof below.
Compare your answer with the correct one above
True or False: The Corresponding Angles Theorem states that if two parallel lines are cut by a transversal then the pair of corresponding angles are supplementary.
True or False: The Corresponding Angles Theorem states that if two parallel lines are cut by a transversal then the pair of corresponding angles are supplementary.
The Corresponding Angles Theorem states that if two parallel lines are cut by a transversal line then the pair of corresponding angles are congruent. Corresponding angles are angles formed when a transversal line cuts two lines and they lie in the same position at each intersection. The figure below illustrates corresponding lines.
The Corresponding Angles Theorem states that if two parallel lines are cut by a transversal line then the pair of corresponding angles are congruent. Corresponding angles are angles formed when a transversal line cuts two lines and they lie in the same position at each intersection. The figure below illustrates corresponding lines.
Compare your answer with the correct one above
Which of the following correctly state the Alternate Interior Angles Theorem?
Which of the following correctly state the Alternate Interior Angles Theorem?
The correct answer is "If two parallel lines are cut by a transversal line, the alternate interior angles are congruent."
Alternate interior angles are pairs of angles on the inner sides of parallel lines but on the opposite sides of a transversal line which is intersecting parallel lines. These angles are always congruent. Alternate interior angles are illustrated in the figure below.
The correct answer is "If two parallel lines are cut by a transversal line, the alternate interior angles are congruent."
Alternate interior angles are pairs of angles on the inner sides of parallel lines but on the opposite sides of a transversal line which is intersecting parallel lines. These angles are always congruent. Alternate interior angles are illustrated in the figure below.
Compare your answer with the correct one above
Prove that if lines 
and 
are parallel, then the same side interior angles, 
and 
, are congruent.
Prove that if lines 
Follow the detailed proof below.
Follow the detailed proof below.
Compare your answer with the correct one above
Prove that angles 1 and 2 are complementary.
Prove that angles 1 and 2 are complementary.
Follow the detailed proof below.
Follow the detailed proof below.
Compare your answer with the correct one above
True or False: Alternate exterior angles are congruent.
True or False: Alternate exterior angles are congruent.
This is true according to the Alternate Exterior Angle Theorem which can be proven in a similar way to the Alternate Interior Angle Theorem. Alternate exterior angles are illustrated in the figure below.
This is true according to the Alternate Exterior Angle Theorem which can be proven in a similar way to the Alternate Interior Angle Theorem. Alternate exterior angles are illustrated in the figure below.
Compare your answer with the correct one above