Construct Inscribed Figures (Equilateral Triangles, Squares, Regular Hexagons) - Common Core: High School - Geometry
Card 0 of 20
Given only the line segment 
, what is the first step to construct a diamond.
Given only the line segment
Given only a line segment there are numerous steps that need to be taken to construct a diamond. Recall a diamond is a parallelogram with four equilateral sides where the diagonals are vertical and horizontal.
The first step in constructing a diamond would be to calculate the length of the line segment 
. After the length is known then the slope can be found and from there, each of the connecting lines can be drawn.
Therefore, the correct answer is,
"Calculate the length of 
."
Given only a line segment there are numerous steps that need to be taken to construct a diamond. Recall a diamond is a parallelogram with four equilateral sides where the diagonals are vertical and horizontal.
The first step in constructing a diamond would be to calculate the length of the line segment
Therefore, the correct answer is,
"Calculate the length of
Compare your answer with the correct one above
Which of the following images is a triangle that is inscribed in a circle?
Which of the following images is a triangle that is inscribed in a circle?
To determine which image illustrates a triangle that is inscribed in a circle, first understand what the term "inscribed" means.
"Inscribed" means to draw inside of. Therefore, a triangle inscribed in a circle means the triangle will be drawn inside of a circle.
The image that illustrates this is as followed.
To determine which image illustrates a triangle that is inscribed in a circle, first understand what the term "inscribed" means.
"Inscribed" means to draw inside of. Therefore, a triangle inscribed in a circle means the triangle will be drawn inside of a circle.
The image that illustrates this is as followed.
Compare your answer with the correct one above
Which of the following images is a circle that is inscribed in a triangle?
Which of the following images is a circle that is inscribed in a triangle?
To determine which image illustrates a circle that is inscribed in a triangle, first understand what the term "inscribed" means.
"Inscribed" means to draw inside of. Therefore, a circle inscribed in a triangle means the circle will be drawn inside of a triangle.
The image that illustrates this is as followed.
To determine which image illustrates a circle that is inscribed in a triangle, first understand what the term "inscribed" means.
"Inscribed" means to draw inside of. Therefore, a circle inscribed in a triangle means the circle will be drawn inside of a triangle.
The image that illustrates this is as followed.
Compare your answer with the correct one above
Which of the following images is a rectangle that is inscribed in a circle?
Which of the following images is a rectangle that is inscribed in a circle?
To determine which image illustrates a rectangle that is inscribed in a circle, first understand what the term "inscribed" means.
"Inscribed" means to draw inside of. Therefore, a rectangle inscribed in a circle means the rectangle will be drawn inside of a circle.
The image that illustrates this is as followed.
To determine which image illustrates a rectangle that is inscribed in a circle, first understand what the term "inscribed" means.
"Inscribed" means to draw inside of. Therefore, a rectangle inscribed in a circle means the rectangle will be drawn inside of a circle.
The image that illustrates this is as followed.
Compare your answer with the correct one above
Which of the following images is a circle that is inscribed in a rectangle?
Which of the following images is a circle that is inscribed in a rectangle?
To determine which image illustrates a circle that is inscribed in a rectangle, first understand what the term "inscribed" means.
"Inscribed" means to draw inside of. Therefore, a circle inscribed in a rectangle means the circle will be drawn inside of a rectangle.
The image that illustrates this is as followed.
To determine which image illustrates a circle that is inscribed in a rectangle, first understand what the term "inscribed" means.
"Inscribed" means to draw inside of. Therefore, a circle inscribed in a rectangle means the circle will be drawn inside of a rectangle.
The image that illustrates this is as followed.
Compare your answer with the correct one above
If a rectangle is inscribed in a circle what can be said about the relationship between the circles diameter and a measurement on the rectangle?
If a rectangle is inscribed in a circle what can be said about the relationship between the circles diameter and a measurement on the rectangle?
First understand what the term "inscribed" means.
"Inscribed" means to draw inside of. Therefore, a rectangle inscribed in a circle means the rectangle will be drawn inside of a circle.
From here the following image can be constructed.
The diameter of the circle is any and all straight lines that cut the circle in half. Since the rectangle is inscribed in that circle and all corners touch the circle then the diameter of the circle is equivalent to the length of the rectangle's diagonal.
First understand what the term "inscribed" means.
"Inscribed" means to draw inside of. Therefore, a rectangle inscribed in a circle means the rectangle will be drawn inside of a circle.
From here the following image can be constructed.
The diameter of the circle is any and all straight lines that cut the circle in half. Since the rectangle is inscribed in that circle and all corners touch the circle then the diameter of the circle is equivalent to the length of the rectangle's diagonal.
Compare your answer with the correct one above
Which of the following images is a pentagon that is inscribed in a circle?
Which of the following images is a pentagon that is inscribed in a circle?
To determine which image illustrates a pentagon that is inscribed in a circle, first understand what the term "inscribed" means.
"Inscribed" means to draw inside of. Therefore, a pentagon inscribed in a circle means the pentagon will be drawn inside of a circle.
The image that illustrates this is as followed.
To determine which image illustrates a pentagon that is inscribed in a circle, first understand what the term "inscribed" means.
"Inscribed" means to draw inside of. Therefore, a pentagon inscribed in a circle means the pentagon will be drawn inside of a circle.
The image that illustrates this is as followed.
Compare your answer with the correct one above
Which of the following images is a circle that is inscribed in a pentagon?
Which of the following images is a circle that is inscribed in a pentagon?
To determine which image illustrates a circle that is inscribed in a pentagon, first understand what the term "inscribed" means.
"Inscribed" means to draw inside of. Therefore, a circle inscribed in a pentagon means the circle will be drawn inside of a pentagon.
The image that illustrates this is as followed.
To determine which image illustrates a circle that is inscribed in a pentagon, first understand what the term "inscribed" means.
"Inscribed" means to draw inside of. Therefore, a circle inscribed in a pentagon means the circle will be drawn inside of a pentagon.
The image that illustrates this is as followed.
Compare your answer with the correct one above
Determine whether the statement is true or false:
For an object to be inscribed in a circle only one of its points must lie within the circle.
Determine whether the statement is true or false:
For an object to be inscribed in a circle only one of its points must lie within the circle.
To determine whether this particular statement is true or false, first understand what the term "inscribed" means.
"Inscribed" means to draw inside of. Therefore, for any object to be inscribed in a circle that means all points of that object must also be inside the circle.
Thus the statement, "For an object to be inscribed in a circle only one of its points must lie within the circle." is false.
To determine whether this particular statement is true or false, first understand what the term "inscribed" means.
"Inscribed" means to draw inside of. Therefore, for any object to be inscribed in a circle that means all points of that object must also be inside the circle.
Thus the statement, "For an object to be inscribed in a circle only one of its points must lie within the circle." is false.
Compare your answer with the correct one above
Determine whether the statement is true or false:
Polygons can be both inscribed inside a circle and have circles inscribed inside of them.
Determine whether the statement is true or false:
Polygons can be both inscribed inside a circle and have circles inscribed inside of them.
To determine whether this particular statement is true or false, first understand what the term "inscribed" means.
"Inscribed" means to draw inside of. Therefore, any and all polygons can be inscribed in a circle and circles can be inscribed in all polygons.
Thus, the statement, "Polygons can be both inscribed inside a circle and have circles inscribed inside of them." is true.
To determine whether this particular statement is true or false, first understand what the term "inscribed" means.
"Inscribed" means to draw inside of. Therefore, any and all polygons can be inscribed in a circle and circles can be inscribed in all polygons.
Thus, the statement, "Polygons can be both inscribed inside a circle and have circles inscribed inside of them." is true.
Compare your answer with the correct one above
Which of the following images is a diamond that is inscribed in a circle?
Which of the following images is a diamond that is inscribed in a circle?
To determine which image illustrates a diamond that is inscribed in a circle, first understand what the term "inscribed" means.
"Inscribed" means to draw inside of. Therefore, a diamond inscribed in a circle means the diamond will be drawn inside of a circle.
The image that illustrates this is as followed.
To determine which image illustrates a diamond that is inscribed in a circle, first understand what the term "inscribed" means.
"Inscribed" means to draw inside of. Therefore, a diamond inscribed in a circle means the diamond will be drawn inside of a circle.
The image that illustrates this is as followed.
Compare your answer with the correct one above
Which of the following images is a circle that is inscribed in a diamond?
Which of the following images is a circle that is inscribed in a diamond?
o determine which image illustrates a circle that is inscribed in a diamond, first understand what the term "inscribed" means.
"Inscribed" means to draw inside of. Therefore, a circle inscribed in a diamond means the circle will be drawn inside of a diamond.
The image that illustrates this is as followed.
o determine which image illustrates a circle that is inscribed in a diamond, first understand what the term "inscribed" means.
"Inscribed" means to draw inside of. Therefore, a circle inscribed in a diamond means the circle will be drawn inside of a diamond.
The image that illustrates this is as followed.
Compare your answer with the correct one above
True or False: An inscribed figure is a shape that fits inside another geometric shape.
True or False: An inscribed figure is a shape that fits inside another geometric shape.
This is true. An inscribed figure is one that fits inside another shape; it can touch the sides of the shape it is inside but it cannot cross over these sides. Below is a circle inscribed in a square. We could also say that the square is circumscribed about the circle.
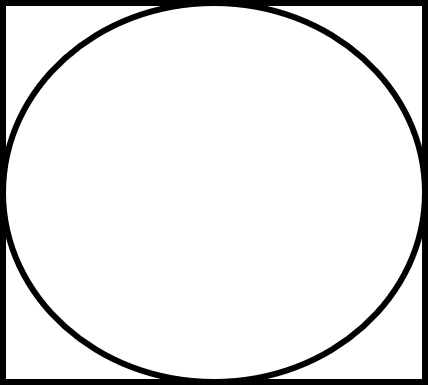
This is true. An inscribed figure is one that fits inside another shape; it can touch the sides of the shape it is inside but it cannot cross over these sides. Below is a circle inscribed in a square. We could also say that the square is circumscribed about the circle.
Compare your answer with the correct one above
How does one find the incenter of a triangle when trying to inscribe a circle within the triangle?
How does one find the incenter of a triangle when trying to inscribe a circle within the triangle?
The incenter is the intersection of the triangle’s three angle bisectors. Drawing two of these angle bisectors is sufficient enough to find the incenter. Below is a figure that illustrates the incenter of a triangle as point A.
The incenter is the intersection of the triangle’s three angle bisectors. Drawing two of these angle bisectors is sufficient enough to find the incenter. Below is a figure that illustrates the incenter of a triangle as point A.
Compare your answer with the correct one above
What are the steps to inscribing an equilateral triangle in a circle?
What are the steps to inscribing an equilateral triangle in a circle?
Explanation: The steps are shown below along with figures for more explanation
1. Make a point at any point on the circle’s circumference
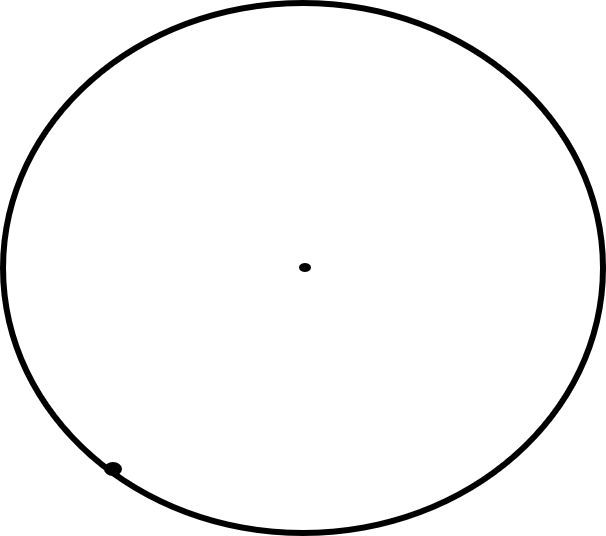
2. Draw an arc across the circle with a compass that is set to the length of the radius, this will be the next vertex
3. Draw arcs in this fashion until there are six vertices
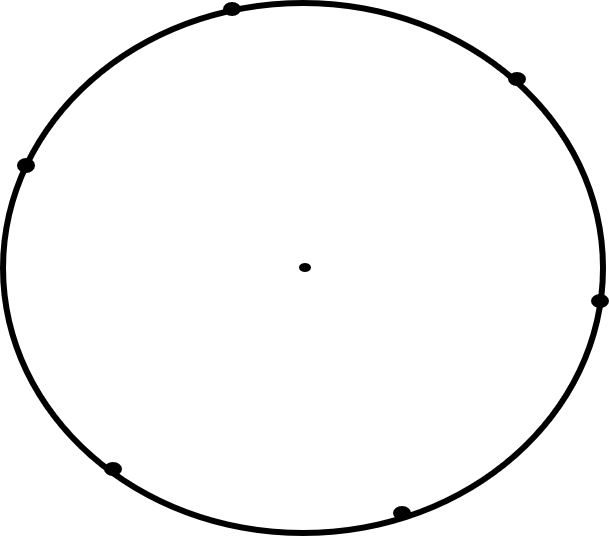
4. Label every other vertex so that there are three vertices
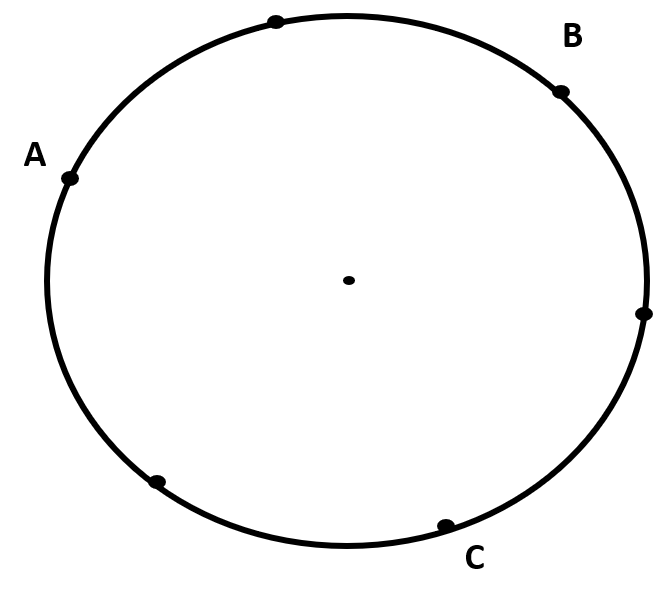
5. Connect these three vertices making three equal sides
Explanation: The steps are shown below along with figures for more explanation
1. Make a point at any point on the circle’s circumference
2. Draw an arc across the circle with a compass that is set to the length of the radius, this will be the next vertex
3. Draw arcs in this fashion until there are six vertices
4. Label every other vertex so that there are three vertices
5. Connect these three vertices making three equal sides
Compare your answer with the correct one above
What are the steps to inscribing a square inside a circle?
What are the steps to inscribing a square inside a circle?
Explanation: The steps are shown below along with figures for more explanation
1. Given a circle (or draw a circle) draw a line across the diameter
2. Draw a line perpendicular to the diameter that also bisects the diameter
3. Label all points that intersect the circumference of the circle
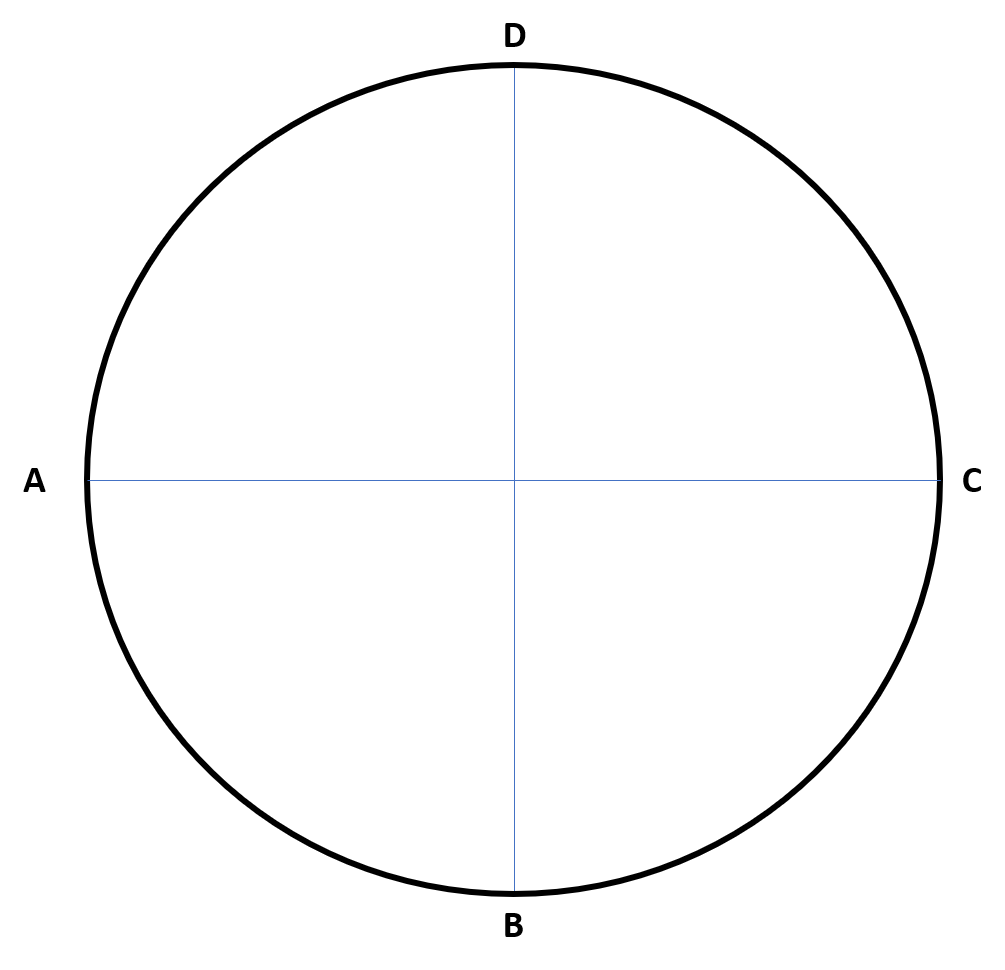
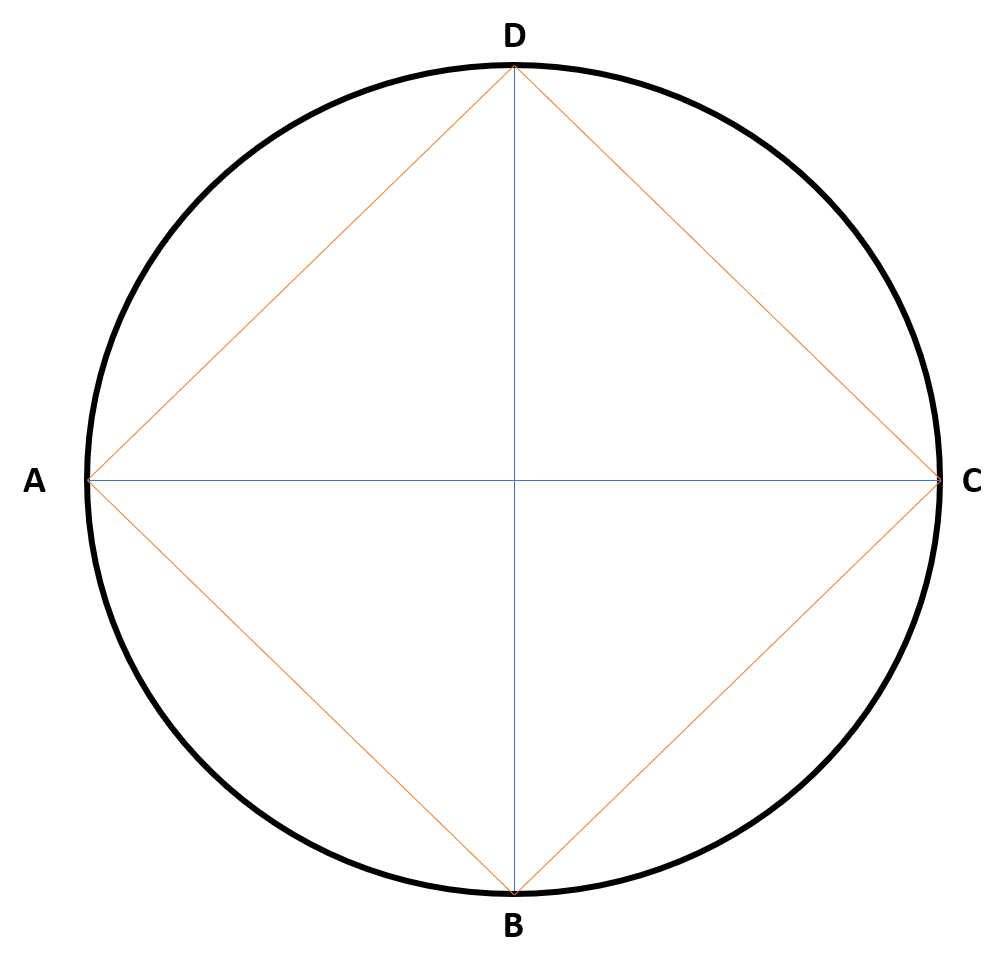
4. Connect the points on the outer edge of the circle to form the four sides of the square
Explanation: The steps are shown below along with figures for more explanation
1. Given a circle (or draw a circle) draw a line across the diameter
2. Draw a line perpendicular to the diameter that also bisects the diameter
3. Label all points that intersect the circumference of the circle
4. Connect the points on the outer edge of the circle to form the four sides of the square
Compare your answer with the correct one above
Which of the following is the correct way to inscribe a square in a right triangle?
Which of the following is the correct way to inscribe a square in a right triangle?
This becomes clear when demonstrated through a picture. Not only does this allow us to inscribe a square within a right triangle, but it also gives us the largest square possible within the right triangle.
This becomes clear when demonstrated through a picture. Not only does this allow us to inscribe a square within a right triangle, but it also gives us the largest square possible within the right triangle.
Compare your answer with the correct one above
Find the side lengths of the square inscribed in the triangle. The area of the entire triangle is 20.
Find the side lengths of the square inscribed in the triangle. The area of the entire triangle is 20.
Since we are finding the side lengths of a square, we really only need to find one side since all sides are congruent in a square. Recall that the formula for the area of a triangle is 
. We can find the area of the square by finding the area of the triangle and subtracting the area of the square. Having the area of the square will just be one of the side lengths squared, so if we take the square root of the area of the square, we will have our answer.
First, consider the small triangle in the upper corner. This is shown below:
The area of this triangle would be
We will consider the lower two triangles combined to be the second triangle:
The area of this triangle would be
And then we need to consider a third area which is the square
The area of the square would be
To get the total area of the triangle, we can sum all three areas.
We can sub in our areas and solve for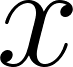 
to solve this problem
(multiply by 2 to get rid of fractions)
Since we are finding the side lengths of a square, we really only need to find one side since all sides are congruent in a square. Recall that the formula for the area of a triangle is 
First, consider the small triangle in the upper corner. This is shown below:
The area of this triangle would be
We will consider the lower two triangles combined to be the second triangle:
The area of this triangle would be
And then we need to consider a third area which is the square
The area of the square would be
To get the total area of the triangle, we can sum all three areas.
We can sub in our areas and solve for
Compare your answer with the correct one above
What are the steps to inscribe a hexagon in a circle?
What are the steps to inscribe a hexagon in a circle?
Explanation: The steps are shown below along with figures for more explanation
1. Make a point at any point on the circle’s circumference
2. Draw an arc across the circle with a compass that is set to the length of the radius, this will be the next vertex
3. Draw arcs in this fashion until there are six vertices
4. These are the six vertices of the hexagon
5. Connect these six vertices making three equal sides
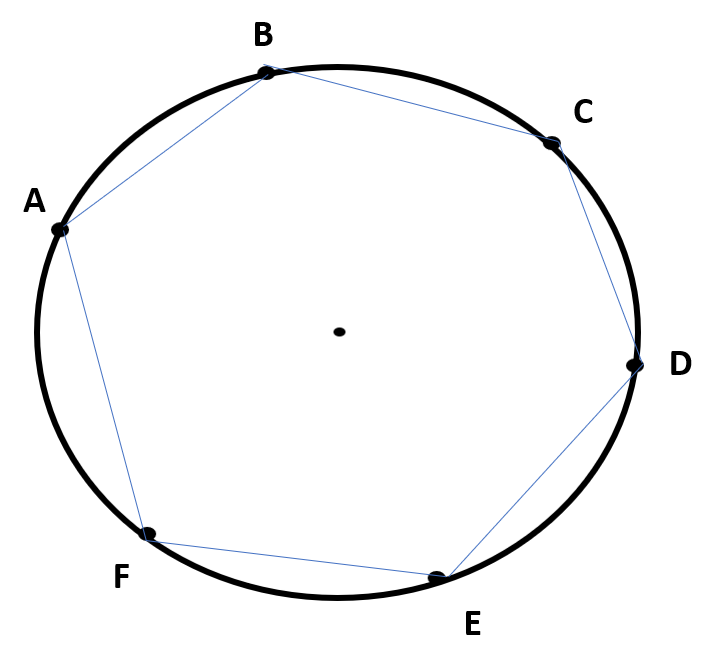
Explanation: The steps are shown below along with figures for more explanation
1. Make a point at any point on the circle’s circumference
2. Draw an arc across the circle with a compass that is set to the length of the radius, this will be the next vertex
3. Draw arcs in this fashion until there are six vertices
4. These are the six vertices of the hexagon
5. Connect these six vertices making three equal sides
Compare your answer with the correct one above
Line 
is perpendicular to line 
where both lines are the diameter of the circle. From this information triangle 
must be a(n) _______ triangle.
Line 
Line 
is perpendicular to line 
and is 90 degrees. We know this because line 
intercepts an arc of 180 degrees. An inscribed angle is half the measure of the intercepted arc. Therefore this must be a right triangle.
Line 
Compare your answer with the correct one above