Graph Square Root, Cube Root, and Piecewise Functions: CCSS.Math.Content.HSF-IF.C.7b - Common Core: High School - Functions
Card 0 of 12
Graph the following function

Graph the following function
This question tests one's ability to graph a square root function.
For the purpose of Common Core Standards, "graph square root, cube root, and piecewise-defined functions, including step functions and absolute value functions" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Make a table of  coordinates for the function.
coordinates for the function.

The values in the table are found by substituting in the x values into the function as follows.

Step 2: Plot the points on a coordinate grid

Step 3: Connect the points with a smooth curve.
Recall that a square root function cannot have negative values under the radical therefore, no x values less than negative four will be in the domain.
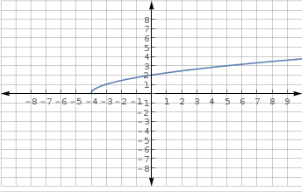
This question tests one's ability to graph a square root function.
For the purpose of Common Core Standards, "graph square root, cube root, and piecewise-defined functions, including step functions and absolute value functions" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Make a table of 
The values in the table are found by substituting in the x values into the function as follows.
Step 2: Plot the points on a coordinate grid

Step 3: Connect the points with a smooth curve.
Recall that a square root function cannot have negative values under the radical therefore, no x values less than negative four will be in the domain.

Compare your answer with the correct one above
Graph the following function.

Graph the following function.
This question tests one's ability to graph a square root function.
For the purpose of Common Core Standards, "graph square root, cube root, and piecewise-defined functions, including step functions and absolute value functions" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Make a table of  coordinates for the function.
coordinates for the function.

The values in the table are found by substituting in the x values into the function as follows.

Step 2: Plot the points on a coordinate grid

Step 3: Connect the points with a smooth curve.
Recall that a square root function cannot have negative values under the radical therefore, no x values more than two will be in the domain.

This question tests one's ability to graph a square root function.
For the purpose of Common Core Standards, "graph square root, cube root, and piecewise-defined functions, including step functions and absolute value functions" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Make a table of 
The values in the table are found by substituting in the x values into the function as follows.
Step 2: Plot the points on a coordinate grid

Step 3: Connect the points with a smooth curve.
Recall that a square root function cannot have negative values under the radical therefore, no x values more than two will be in the domain.

Compare your answer with the correct one above
Graph the following function.

Graph the following function.
This question tests one's ability to graph a square root function.
For the purpose of Common Core Standards, "graph square root, cube root, and piecewise-defined functions, including step functions and absolute value functions" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Make a table of  coordinates for the function.
coordinates for the function.

The values in the table are found by substituting in the x values into the function as follows.

Step 2: Plot the points on a coordinate grid

Step 3: Connect the points with a smooth curve.
Recall that a square root function cannot have negative values under the radical therefore, no x values greater than one will be in the domain.

This question tests one's ability to graph a square root function.
For the purpose of Common Core Standards, "graph square root, cube root, and piecewise-defined functions, including step functions and absolute value functions" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Make a table of 
The values in the table are found by substituting in the x values into the function as follows.
Step 2: Plot the points on a coordinate grid

Step 3: Connect the points with a smooth curve.
Recall that a square root function cannot have negative values under the radical therefore, no x values greater than one will be in the domain.

Compare your answer with the correct one above
Graph the following function.

Graph the following function.
This question tests one's ability to graph a square root function.
For the purpose of Common Core Standards, "graph square root, cube root, and piecewise-defined functions, including step functions and absolute value functions" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Make a table of  coordinates for the function.
coordinates for the function.

The values in the table are found by substituting in the x values into the function as follows.

Step 2: Plot the points on a coordinate grid and connect them with a smooth curve.
Recall that a square root function cannot have negative values under the radical therefore, no x values less than zero will be in the domain.

This question tests one's ability to graph a square root function.
For the purpose of Common Core Standards, "graph square root, cube root, and piecewise-defined functions, including step functions and absolute value functions" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Make a table of 
The values in the table are found by substituting in the x values into the function as follows.
Step 2: Plot the points on a coordinate grid and connect them with a smooth curve.
Recall that a square root function cannot have negative values under the radical therefore, no x values less than zero will be in the domain.

Compare your answer with the correct one above
Graph the following function.

Graph the following function.
This question tests one's ability to graph a square root function.
For the purpose of Common Core Standards, "graph square root, cube root, and piecewise-defined functions, including step functions and absolute value functions" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Make a table of  coordinates for the function.
coordinates for the function.

The values in the table are found by substituting in the x values into the function as follows.

Step 2: Plot the points on a coordinate grid and connect them with a smooth curve.
Recall that a square root function cannot have negative values under the radical therefore, no x values less than negative two will be in the domain.

This question tests one's ability to graph a square root function.
For the purpose of Common Core Standards, "graph square root, cube root, and piecewise-defined functions, including step functions and absolute value functions" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Make a table of 
The values in the table are found by substituting in the x values into the function as follows.
Step 2: Plot the points on a coordinate grid and connect them with a smooth curve.
Recall that a square root function cannot have negative values under the radical therefore, no x values less than negative two will be in the domain.

Compare your answer with the correct one above
Graph the following function.

Graph the following function.
This question tests one's ability to graph a square root function.
For the purpose of Common Core Standards, "graph square root, cube root, and piecewise-defined functions, including step functions and absolute value functions" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Make a table of  coordinates for the function.
coordinates for the function.

The values in the table are found by substituting in the x values into the function as follows.

Step 2: Plot the points on a coordinate grid and connect them with a smooth curve.
Recall that a square root function cannot have negative values under the radical therefore, no x values less than two will be in the domain.

This question tests one's ability to graph a square root function.
For the purpose of Common Core Standards, "graph square root, cube root, and piecewise-defined functions, including step functions and absolute value functions" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Make a table of 
The values in the table are found by substituting in the x values into the function as follows.
Step 2: Plot the points on a coordinate grid and connect them with a smooth curve.
Recall that a square root function cannot have negative values under the radical therefore, no x values less than two will be in the domain.

Compare your answer with the correct one above
Graph the following function.

Graph the following function.
This question tests one's ability to graph a square root function.
For the purpose of Common Core Standards, "graph square root, cube root, and piecewise-defined functions, including step functions and absolute value functions" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Make a table of  coordinates for the function.
coordinates for the function.

The values in the table are found by substituting in the x values into the function as follows.

Step 2: Plot the points on a coordinate grid and connect them with a smooth curve.
Recall that a square root function cannot have negative values under the radical therefore, no x values less than three will be in the domain.

This question tests one's ability to graph a square root function.
For the purpose of Common Core Standards, "graph square root, cube root, and piecewise-defined functions, including step functions and absolute value functions" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Make a table of 
The values in the table are found by substituting in the x values into the function as follows.
Step 2: Plot the points on a coordinate grid and connect them with a smooth curve.
Recall that a square root function cannot have negative values under the radical therefore, no x values less than three will be in the domain.

Compare your answer with the correct one above
Graph the following function.

Graph the following function.
This question tests one's ability to graph a square root function.
For the purpose of Common Core Standards, "graph square root, cube root, and piecewise-defined functions, including step functions and absolute value functions" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Make a table of  coordinates for the function.
coordinates for the function.

The values in the table are found by substituting in the x values into the function as follows.

Step 2: Plot the points on a coordinate grid and connect them with a smooth curve.
Recall that a square root function cannot have negative values under the radical therefore, no x values less than zero will be in the domain.

This question tests one's ability to graph a square root function.
For the purpose of Common Core Standards, "graph square root, cube root, and piecewise-defined functions, including step functions and absolute value functions" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Make a table of 
The values in the table are found by substituting in the x values into the function as follows.
Step 2: Plot the points on a coordinate grid and connect them with a smooth curve.
Recall that a square root function cannot have negative values under the radical therefore, no x values less than zero will be in the domain.

Compare your answer with the correct one above
Graph the following function.

Graph the following function.
This question tests one's ability to graph a square root function.
For the purpose of Common Core Standards, "graph square root, cube root, and piecewise-defined functions, including step functions and absolute value functions" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Make a table of  coordinates for the function.
coordinates for the function.

The values in the table are found by substituting in the x values into the function as follows.

Step 2: Plot the points on a coordinate grid and connect them with a smooth curve.
Recall that a square root function cannot have negative values under the radical therefore, no x values less than zero will be in the domain.

This question tests one's ability to graph a square root function.
For the purpose of Common Core Standards, "graph square root, cube root, and piecewise-defined functions, including step functions and absolute value functions" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Make a table of 
The values in the table are found by substituting in the x values into the function as follows.
Step 2: Plot the points on a coordinate grid and connect them with a smooth curve.
Recall that a square root function cannot have negative values under the radical therefore, no x values less than zero will be in the domain.

Compare your answer with the correct one above
Graph the following function.

Graph the following function.
This question tests one's ability to graph a square root function.
For the purpose of Common Core Standards, "graph square root, cube root, and piecewise-defined functions, including step functions and absolute value functions" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Make a table of  coordinates for the function.
coordinates for the function.

The values in the table are found by substituting in the x values into the function as follows.

Step 2: Plot the points on a coordinate grid and connect them with a smooth curve.
Recall that a square root function cannot have negative values under the radical therefore, no x values less than one half will be in the domain.

This question tests one's ability to graph a square root function.
For the purpose of Common Core Standards, "graph square root, cube root, and piecewise-defined functions, including step functions and absolute value functions" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Make a table of 
The values in the table are found by substituting in the x values into the function as follows.
Step 2: Plot the points on a coordinate grid and connect them with a smooth curve.
Recall that a square root function cannot have negative values under the radical therefore, no x values less than one half will be in the domain.

Compare your answer with the correct one above
Graph the following function.

Graph the following function.
This question tests one's ability to graph a square root function.
For the purpose of Common Core Standards, "graph square root, cube root, and piecewise-defined functions, including step functions and absolute value functions" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Make a table of  coordinates for the function.
coordinates for the function.

The values in the table are found by substituting in the x values into the function as follows.

Step 2: Plot the points on a coordinate grid and connect them with a smooth curve.
Recall that a square root function cannot have negative values under the radical therefore, no x values greater than zero will be in the domain.

This question tests one's ability to graph a square root function.
For the purpose of Common Core Standards, "graph square root, cube root, and piecewise-defined functions, including step functions and absolute value functions" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Make a table of 
The values in the table are found by substituting in the x values into the function as follows.
Step 2: Plot the points on a coordinate grid and connect them with a smooth curve.
Recall that a square root function cannot have negative values under the radical therefore, no x values greater than zero will be in the domain.

Compare your answer with the correct one above
Graph the following function.

Graph the following function.
This question tests one's ability to graph a square root function.
For the purpose of Common Core Standards, "graph square root, cube root, and piecewise-defined functions, including step functions and absolute value functions" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Make a table of  coordinates for the function.
coordinates for the function.

The values in the table are found by substituting in the x values into the function as follows.

Step 2: Plot the points on a coordinate grid and connect them with a smooth curve.
Recall that a square root function cannot have negative values under the radical therefore, no x values greater than zero will be in the domain.

This question tests one's ability to graph a square root function.
For the purpose of Common Core Standards, "graph square root, cube root, and piecewise-defined functions, including step functions and absolute value functions" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Make a table of 
The values in the table are found by substituting in the x values into the function as follows.
Step 2: Plot the points on a coordinate grid and connect them with a smooth curve.
Recall that a square root function cannot have negative values under the radical therefore, no x values greater than zero will be in the domain.

Compare your answer with the correct one above