Understand Linear and Nonlinear Functions: CCSS.Math.Content.8.F.A.3 - Common Core: 8th Grade Math
Card 0 of 18
Which of the following graphs matches the function  ?
?
Which of the following graphs matches the function 
Start by visualizing the graph associated with the function  :
:

Terms within the parentheses associated with the squared x-variable will shift the parabola horizontally, while terms outside of the parentheses will shift the parabola vertically. In the provided equation, 2 is located outside of the parentheses and is subtracted from the terms located within the parentheses; therefore, the parabola in the graph will shift down by 2 units. A simplified graph of  looks like this:
looks like this:

Remember that there is also a term within the parentheses. Within the parentheses, 1 is subtracted from the x-variable; thus, the parabola in the graph will shift to the right by 1 unit. As a result, the following graph matches the given function  :
:

Start by visualizing the graph associated with the function 

Terms within the parentheses associated with the squared x-variable will shift the parabola horizontally, while terms outside of the parentheses will shift the parabola vertically. In the provided equation, 2 is located outside of the parentheses and is subtracted from the terms located within the parentheses; therefore, the parabola in the graph will shift down by 2 units. A simplified graph of 

Remember that there is also a term within the parentheses. Within the parentheses, 1 is subtracted from the x-variable; thus, the parabola in the graph will shift to the right by 1 unit. As a result, the following graph matches the given function 

Compare your answer with the correct one above
Which equation best represents the following graph?
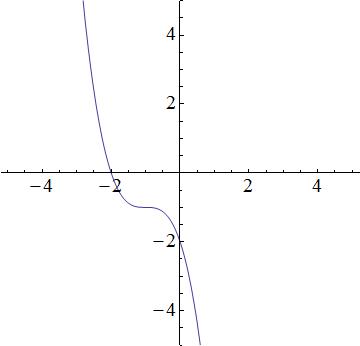
Which equation best represents the following graph?

We have the following answer choices.




The first equation is a cubic function, which produces a function similar to the graph. The second equation is quadratic and thus, a parabola. The graph does not look like a prabola, so the 2nd equation will be incorrect. The third equation describes a line, but the graph is not linear; the third equation is incorrect. The fourth equation is incorrect because it is an exponential, and the graph is not an exponential. So that leaves the first equation as the best possible choice.
We have the following answer choices.
The first equation is a cubic function, which produces a function similar to the graph. The second equation is quadratic and thus, a parabola. The graph does not look like a prabola, so the 2nd equation will be incorrect. The third equation describes a line, but the graph is not linear; the third equation is incorrect. The fourth equation is incorrect because it is an exponential, and the graph is not an exponential. So that leaves the first equation as the best possible choice.
Compare your answer with the correct one above
For the graph below, match the graph b with one of the following equations:








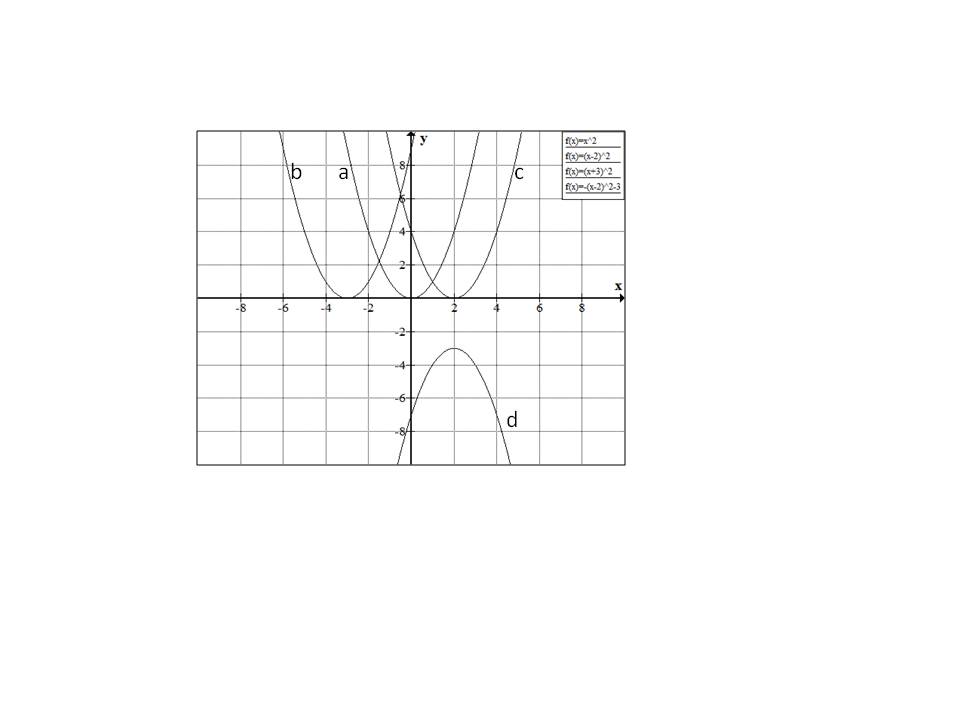
For the graph below, match the graph b with one of the following equations:





Starting with 
 moves the parabola
moves the parabola  by
by  units to the right.
units to the right.
Similarly  moves the parabola by
moves the parabola by  units to the left.
units to the left.
Hence the correct answer is option  .
.
Starting with



Similarly 

Hence the correct answer is option 
Compare your answer with the correct one above
Which graph depicts a function?
Which graph depicts a function?
A function may only have one y-value for each x-value.
The vertical line test can be used to identify the function. If at any point on the graph, a straight vertical line intersects the curve at more than one point, the curve is not a function.
A function may only have one y-value for each x-value.
The vertical line test can be used to identify the function. If at any point on the graph, a straight vertical line intersects the curve at more than one point, the curve is not a function.
Compare your answer with the correct one above
Which of the graphs best represents the following function?

Which of the graphs best represents the following function?

The highest exponent of the variable term is two ( ). This tells that this function is quadratic, meaning that it is a parabola.
). This tells that this function is quadratic, meaning that it is a parabola.
The graph below will be the answer, as it shows a parabolic curve.

The highest exponent of the variable term is two (
The graph below will be the answer, as it shows a parabolic curve.

Compare your answer with the correct one above
What is the equation of a parabola with vertex  and
and  -intercept
-intercept  ?
?
What is the equation of a parabola with vertex 


From the vertex, we know that the equation of the parabola will take the form  for some
for some  .
.
To calculate that  , we plug in the values from the other point we are given,
, we plug in the values from the other point we are given,  , and solve for
, and solve for  :
:






Now the equation is  . This is not an answer choice, so we need to rewrite it in some way.
. This is not an answer choice, so we need to rewrite it in some way.
Expand the squared term:

Distribute the fraction through the parentheses:

Combine like terms:

From the vertex, we know that the equation of the parabola will take the form 

To calculate that 


Now the equation is 
Expand the squared term:
Distribute the fraction through the parentheses:
Combine like terms:
Compare your answer with the correct one above
Select the equation that best represents a linear function.
Select the equation that best represents a linear function.
In order to determine if an equation defines a linear function, we want to make sure that the equation of the line is in slope-intercept form:

If we are unable to put an equation in this form, then the equation is not linear.
Let's take a look at our answer choices:

Notice that in this equation our  value is to the third power, which does not match our slope-intercept form.
value is to the third power, which does not match our slope-intercept form.

Though this equation is not written in  form, we can tell straight away that this does not define a linear function because the
form, we can tell straight away that this does not define a linear function because the  value is to the second power.
value is to the second power.

Again, though this equation is not written in  form, we can tell straight away that this does not define a linear function because the
form, we can tell straight away that this does not define a linear function because the  value is to the second power.
value is to the second power.

For this equation, we can solve for  to make sure this equation can be written is slope-intercept form. From first glance it looks to be correct because none of our variables are written to a power. In order to tell for certain, we need to isolate the y variable on the left side of the equation.
to make sure this equation can be written is slope-intercept form. From first glance it looks to be correct because none of our variables are written to a power. In order to tell for certain, we need to isolate the y variable on the left side of the equation.
First, we can subtract  from both sides:
from both sides:
![\frac{\begin{array}[b]{r}6y+4x=16\ -4x-4x\end{array}}{\\6y=-4x+16}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/963213/gif.latex)
Next, we can divide each side by 


This equation is in slope-intercept form; thus,  is the correct answer.
is the correct answer.
In order to determine if an equation defines a linear function, we want to make sure that the equation of the line is in slope-intercept form:
If we are unable to put an equation in this form, then the equation is not linear.
Let's take a look at our answer choices:
Notice that in this equation our 
Though this equation is not written in 

Again, though this equation is not written in 

For this equation, we can solve for 
First, we can subtract 
Next, we can divide each side by
This equation is in slope-intercept form; thus, 
Compare your answer with the correct one above
Select the equation that best represents a linear function.
Select the equation that best represents a linear function.
In order to determine if an equation defines a linear function, we want to make sure that the equation of the line is in slope-intercept form:

If we are unable to put an equation in this form, then the equation is not linear.
Let's take a look at our answer choices:

Notice that in this equation our  value is to the third power, which does not match our slope-intercept form.
value is to the third power, which does not match our slope-intercept form.

Though this equation is not written in  form, we can tell straight away that this does not define a linear function because the
form, we can tell straight away that this does not define a linear function because the  value is to the second power.
value is to the second power.

Again, though this equation is not written in  form, we can tell straight away that this does not define a linear function because the
form, we can tell straight away that this does not define a linear function because the  value is to the second power.
value is to the second power.

For this equation, we can solve for  to make sure this equation can be written is slope-intercept form. From first glance it looks to be correct because none of our variables are written to a power. In order to tell for certain, we need to isolate the y variable on the left side of the equation.
to make sure this equation can be written is slope-intercept form. From first glance it looks to be correct because none of our variables are written to a power. In order to tell for certain, we need to isolate the y variable on the left side of the equation.
We can add  to both sides:
to both sides:
![\frac{\begin{array}[b]{r}y-2x=6\ +2x+2x\end{array}}{\\y=2x+6}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/963326/gif.latex)
This equation is in slope-intercept form; thus,  is the correct answer.
is the correct answer.
In order to determine if an equation defines a linear function, we want to make sure that the equation of the line is in slope-intercept form:
If we are unable to put an equation in this form, then the equation is not linear.
Let's take a look at our answer choices:
Notice that in this equation our 
Though this equation is not written in 

Again, though this equation is not written in 

For this equation, we can solve for 
We can add 
This equation is in slope-intercept form; thus, 
Compare your answer with the correct one above
Select the equation that best represents a linear function.
Select the equation that best represents a linear function.
In order to determine if an equation defines a linear function, we want to make sure that the equation of the line is in slope-intercept form:

If we are unable to put an equation in this form, then the equation is not linear.
Let's take a look at our answer choices:

Notice that in this equation our  value is to the third power, which does not match our slope-intercept form.
value is to the third power, which does not match our slope-intercept form.

Though this equation is not written in  form, we can tell straight away that this does not define a linear function because the
form, we can tell straight away that this does not define a linear function because the  value is to the second power.
value is to the second power.

Again, though this equation is not written in  form, we can tell straight away that this does not define a linear function because the
form, we can tell straight away that this does not define a linear function because the  value is to the second power.
value is to the second power.

For this equation, we can solve for  to make sure this equation can be written is slope-intercept form. From first glance it looks to be correct because none of our variables are written to a power. In order to tell for certain, we need to isolate the y variable on the left side of the equation.
to make sure this equation can be written is slope-intercept form. From first glance it looks to be correct because none of our variables are written to a power. In order to tell for certain, we need to isolate the y variable on the left side of the equation.
We can add  to both sides:
to both sides:
![\frac{\begin{array}[b]{r}y-3x=4x+3\ +3x+3x\ \ \ \ \ \end{array}}{\\y=7x+3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/963260/gif.latex)
This equation is in slope-intercept form; thus,  is the correct answer.
is the correct answer.
In order to determine if an equation defines a linear function, we want to make sure that the equation of the line is in slope-intercept form:
If we are unable to put an equation in this form, then the equation is not linear.
Let's take a look at our answer choices:
Notice that in this equation our 
Though this equation is not written in 

Again, though this equation is not written in 

For this equation, we can solve for 
We can add 
This equation is in slope-intercept form; thus, 
Compare your answer with the correct one above
Select the equation that best represents a linear function.
Select the equation that best represents a linear function.
In order to determine if an equation defines a linear function, we want to make sure that the equation of the line is in slope-intercept form:

If we are unable to put an equation in this form, then the equation is not linear.
Let's take a look at our answer choices:

Notice that in this equation our  value is to the third power, which does not match our slope-intercept form.
value is to the third power, which does not match our slope-intercept form.

Though this equation is not written in  form, we can tell straight away that this does not define a linear function because the
form, we can tell straight away that this does not define a linear function because the  value is to the second power.
value is to the second power.

Again, though this equation is not written in  form, we can tell straight away that this does not define a linear function because the
form, we can tell straight away that this does not define a linear function because the  value is to the second power.
value is to the second power.

For this equation, we can solve for  to make sure this equation can be written is slope-intercept form. From first glance it looks to be correct because none of our variables are written to a power. In order to tell for certain, we need to isolate the y variable on the left side of the equation.
to make sure this equation can be written is slope-intercept form. From first glance it looks to be correct because none of our variables are written to a power. In order to tell for certain, we need to isolate the y variable on the left side of the equation.
First, we can subtract  from both sides:
from both sides:
![\frac{\begin{array}[b]{r}2y+4x=8x+20\ -4x-4x\ \ \ \ \ \ \end{array}}{\\2y=4x+20}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/963295/gif.latex)
Next, we can divide each side by 


This equation is in slope-intercept form; thus,  is the correct answer.
is the correct answer.
In order to determine if an equation defines a linear function, we want to make sure that the equation of the line is in slope-intercept form:
If we are unable to put an equation in this form, then the equation is not linear.
Let's take a look at our answer choices:
Notice that in this equation our 
Though this equation is not written in 

Again, though this equation is not written in 

For this equation, we can solve for 
First, we can subtract 
Next, we can divide each side by
This equation is in slope-intercept form; thus, 
Compare your answer with the correct one above
Select the equation that best represents a linear function.
Select the equation that best represents a linear function.
In order to determine if an equation defines a linear function, we want to make sure that the equation of the line is in slope-intercept form:

If we are unable to put an equation in this form, then the equation is not linear.
Let's take a look at our answer choices:

Notice that in this equation our  value is to the third power, which does not match our slope-intercept form.
value is to the third power, which does not match our slope-intercept form.

Though this equation is not written in  form, we can tell straight away that this does not define a linear function because the
form, we can tell straight away that this does not define a linear function because the  value is to the second power.
value is to the second power.

Again, though this equation is not written in  form, we can tell straight away that this does not define a linear function because the
form, we can tell straight away that this does not define a linear function because the  value is to the second power.
value is to the second power.

For this equation, we can solve for  to make sure this equation can be written is slope-intercept form. From first glance it looks to be correct because none of our variables are written to a power. In order to tell for certain, we need to isolate the y variable on the left side of the equation.
to make sure this equation can be written is slope-intercept form. From first glance it looks to be correct because none of our variables are written to a power. In order to tell for certain, we need to isolate the y variable on the left side of the equation.
First, we can subtract  from both sides:
from both sides:
![\frac{\begin{array}[b]{r}y+9x=3x+17\ -9x-9x\ \ \ \ \ \ \ \end{array}}{\\y=-6x+17}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/963284/gif.latex)
This equation is in slope-intercept form; thus,  is the correct answer.
is the correct answer.
In order to determine if an equation defines a linear function, we want to make sure that the equation of the line is in slope-intercept form:
If we are unable to put an equation in this form, then the equation is not linear.
Let's take a look at our answer choices:
Notice that in this equation our 
Though this equation is not written in 

Again, though this equation is not written in 

For this equation, we can solve for 
First, we can subtract 
This equation is in slope-intercept form; thus, 
Compare your answer with the correct one above
Select the equation that best represents a linear function.
Select the equation that best represents a linear function.
In order to determine if an equation defines a linear function, we want to make sure that the equation of the line is in slope-intercept form:

If we are unable to put an equation in this form, then the equation is not linear.
Let's take a look at our answer choices:

Notice that in this equation our  value is to the third power, which does not match our slope-intercept form.
value is to the third power, which does not match our slope-intercept form.

Though this equation is not written in  form, we can tell straight away that this does not define a linear function because the
form, we can tell straight away that this does not define a linear function because the  value is to the second power.
value is to the second power.

Again, though this equation is not written in  form, we can tell straight away that this does not define a linear function because the
form, we can tell straight away that this does not define a linear function because the  value is to the second power.
value is to the second power.

For this equation, we can solve for  to make sure this equation can be written is slope-intercept form. From first glance it looks to be correct because none of our variables are written to a power. In order to tell for certain, we need to isolate the y variable on the left side of the equation.
to make sure this equation can be written is slope-intercept form. From first glance it looks to be correct because none of our variables are written to a power. In order to tell for certain, we need to isolate the y variable on the left side of the equation.
First, we can subtract  from both sides:
from both sides:
![\frac{\begin{array}[b]{r}3y+12x=-6x+9\ -12x-12x\ \ \ \ \ \end{array}}{\\3y=-18x+9}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/963316/gif.latex)
Next, we can divide each side by 


This equation is in slope-intercept form; thus,  is the correct answer.
is the correct answer.
In order to determine if an equation defines a linear function, we want to make sure that the equation of the line is in slope-intercept form:
If we are unable to put an equation in this form, then the equation is not linear.
Let's take a look at our answer choices:
Notice that in this equation our 
Though this equation is not written in 

Again, though this equation is not written in 

For this equation, we can solve for 
First, we can subtract 
Next, we can divide each side by
This equation is in slope-intercept form; thus, 
Compare your answer with the correct one above
Select the equation that best represents a linear function.
Select the equation that best represents a linear function.
In order to determine if an equation defines a linear function, we want to make sure that the equation of the line is in slope-intercept form:

If we are unable to put an equation in this form, then the equation is not linear.
Let's take a look at our answer choices:

Notice that in this equation our  value is to the third power, which does not match our slope-intercept form.
value is to the third power, which does not match our slope-intercept form.

Though this equation is not written in  form, we can tell straight away that this does not define a linear function because the
form, we can tell straight away that this does not define a linear function because the  value is to the second power.
value is to the second power.

Again, though this equation is not written in  form, we can tell straight away that this does not define a linear function because the
form, we can tell straight away that this does not define a linear function because the  value is to the second power.
value is to the second power.

For this equation, we can solve for  to make sure this equation can be written is slope-intercept form. From first glance it looks to be correct because none of our variables are written to a power. In order to tell for certain, we need to isolate the y variable on the left side of the equation.
to make sure this equation can be written is slope-intercept form. From first glance it looks to be correct because none of our variables are written to a power. In order to tell for certain, we need to isolate the y variable on the left side of the equation.
First, we can subtract  from both sides:
from both sides:
![\frac{\begin{array}[b]{r}y+8x=24\ -8x-8x\end{array}}{\\y=-8x+24}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/963337/gif.latex)
This equation is in slope-intercept form; thus,  is the correct answer.
is the correct answer.
In order to determine if an equation defines a linear function, we want to make sure that the equation of the line is in slope-intercept form:
If we are unable to put an equation in this form, then the equation is not linear.
Let's take a look at our answer choices:
Notice that in this equation our 
Though this equation is not written in 

Again, though this equation is not written in 

For this equation, we can solve for 
First, we can subtract 
This equation is in slope-intercept form; thus, 
Compare your answer with the correct one above
Select the equation that best represents a linear function.
Select the equation that best represents a linear function.
In order to determine if an equation defines a linear function, we want to make sure that the equation of the line is in slope-intercept form:

If we are unable to put an equation in this form, then the equation is not linear.
Let's take a look at our answer choices:

Notice that in this equation our  value is to the third power, which does not match our slope-intercept form.
value is to the third power, which does not match our slope-intercept form.

Though this equation is not written in  form, we can tell straight away that this does not define a linear function because the
form, we can tell straight away that this does not define a linear function because the  value is to the second power.
value is to the second power.

Again, though this equation is not written in  form, we can tell straight away that this does not define a linear function because the
form, we can tell straight away that this does not define a linear function because the  value is to the second power.
value is to the second power.

This equation is in slope-intercept form; thus,  is the correct answer.
is the correct answer.
In order to determine if an equation defines a linear function, we want to make sure that the equation of the line is in slope-intercept form:
If we are unable to put an equation in this form, then the equation is not linear.
Let's take a look at our answer choices:
Notice that in this equation our 
Though this equation is not written in 

Again, though this equation is not written in 

This equation is in slope-intercept form; thus, 
Compare your answer with the correct one above
Select the equation that best represents a linear function.
Select the equation that best represents a linear function.
In order to determine if an equation defines a linear function, we want to make sure that the equation of the line is in slope-intercept form:

If we are unable to put an equation in this form, then the equation is not linear.
Let's take a look at our answer choices:

Notice that in this equation our  value is to the third power, which does not match our slope-intercept form.
value is to the third power, which does not match our slope-intercept form.

Though this equation is not written in  form, we can tell straight away that this does not define a linear function because the
form, we can tell straight away that this does not define a linear function because the  value is to the second power.
value is to the second power.

Again, though this equation is not written in  form, we can tell straight away that this does not define a linear function because the
form, we can tell straight away that this does not define a linear function because the  value is to the second power.
value is to the second power.

This equation is in slope-intercept form; thus,  is the correct answer.
is the correct answer.
In order to determine if an equation defines a linear function, we want to make sure that the equation of the line is in slope-intercept form:
If we are unable to put an equation in this form, then the equation is not linear.
Let's take a look at our answer choices:
Notice that in this equation our 
Though this equation is not written in 

Again, though this equation is not written in 

This equation is in slope-intercept form; thus, 
Compare your answer with the correct one above
Select the equation that best represents a linear function.
Select the equation that best represents a linear function.
In order to determine if an equation defines a linear function, we want to make sure that the equation of the line is in slope-intercept form:

If we are unable to put an equation in this form, then the equation is not linear.
Let's take a look at our answer choices:

Notice that in this equation our  value is to the third power, which does not match our slope-intercept form.
value is to the third power, which does not match our slope-intercept form.

Though this equation is not written in  form, we can tell straight away that this does not define a linear function because the
form, we can tell straight away that this does not define a linear function because the  value is to the second power.
value is to the second power.

Again, though this equation is not written in  form, we can tell straight away that this does not define a linear function because the
form, we can tell straight away that this does not define a linear function because the  value is to the second power.
value is to the second power.

For this equation, we can solve for  to make sure this equation can be written is slope-intercept form. From first glance it looks to be correct because none of our variables are written to a power. In order to tell for certain, we need to isolate the y variable on the left side of the equation.
to make sure this equation can be written is slope-intercept form. From first glance it looks to be correct because none of our variables are written to a power. In order to tell for certain, we need to isolate the y variable on the left side of the equation.
First, we can subtract  from both sides:
from both sides:
![\frac{\begin{array}[b]{r}y+6x=2x-14\ -6x-6x\ \ \ \ \ \ \ \end{array}}{\\y=-4x+14}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/963507/gif.latex)
This equation is in slope-intercept form; thus,  is the correct answer.
is the correct answer.
In order to determine if an equation defines a linear function, we want to make sure that the equation of the line is in slope-intercept form:
If we are unable to put an equation in this form, then the equation is not linear.
Let's take a look at our answer choices:
Notice that in this equation our 
Though this equation is not written in 

Again, though this equation is not written in 

For this equation, we can solve for 
First, we can subtract 
This equation is in slope-intercept form; thus, 
Compare your answer with the correct one above
Select the equation that best represents a linear function.
Select the equation that best represents a linear function.
In order to determine if an equation defines a linear function, we want to make sure that the equation of the line is in slope-intercept form:

If we are unable to put an equation in this form, then the equation is not linear.
Let's take a look at our answer choices:

Notice that in this equation our  value is to the third power, which does not match our slope-intercept form.
value is to the third power, which does not match our slope-intercept form.

Though this equation is not written in  form, we can tell straight away that this does not define a linear function because the
form, we can tell straight away that this does not define a linear function because the  value is to the second power.
value is to the second power.

Again, though this equation is not written in  form, we can tell straight away that this does not define a linear function because the
form, we can tell straight away that this does not define a linear function because the  value is to the second power.
value is to the second power.

For this equation, we can solve for  to make sure this equation can be written is slope-intercept form. From first glance it looks to be correct because none of our variables are written to a power. In order to tell for certain, we need to isolate the y variable on the left side of the equation.
to make sure this equation can be written is slope-intercept form. From first glance it looks to be correct because none of our variables are written to a power. In order to tell for certain, we need to isolate the y variable on the left side of the equation.
First, we can subtract  from both sides:
from both sides:
![\frac{\begin{array}[b]{r}3y+12x=21\ -12x-12x\end{array}}{\\3y=-12x+21}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/963514/gif.latex)
Next, we can divide each side by 


This equation is in slope-intercept form; thus,  is the correct answer.
is the correct answer.
In order to determine if an equation defines a linear function, we want to make sure that the equation of the line is in slope-intercept form:
If we are unable to put an equation in this form, then the equation is not linear.
Let's take a look at our answer choices:
Notice that in this equation our 
Though this equation is not written in 

Again, though this equation is not written in 

For this equation, we can solve for 
First, we can subtract 
Next, we can divide each side by
This equation is in slope-intercept form; thus, 
Compare your answer with the correct one above
Select the equation that best represents a linear function.
Select the equation that best represents a linear function.
In order to determine if an equation defines a linear function, we want to make sure that the equation of the line is in slope-intercept form:

If we are unable to put an equation in this form, then the equation is not linear.
Let's take a look at our answer choices:

Notice that in this equation our  value is to the third power, which does not match our slope-intercept form.
value is to the third power, which does not match our slope-intercept form.

Though this equation is not written in  form, we can tell straight away that this does not define a linear function because the
form, we can tell straight away that this does not define a linear function because the  value is to the second power.
value is to the second power.

Again, though this equation is not written in  form, we can tell straight away that this does not define a linear function because the
form, we can tell straight away that this does not define a linear function because the  value is to the second power.
value is to the second power.

This equation is in slope-intercept form; thus,  is the correct answer.
is the correct answer.
In order to determine if an equation defines a linear function, we want to make sure that the equation of the line is in slope-intercept form:
If we are unable to put an equation in this form, then the equation is not linear.
Let's take a look at our answer choices:
Notice that in this equation our 
Though this equation is not written in 

Again, though this equation is not written in 

This equation is in slope-intercept form; thus, 
Compare your answer with the correct one above