Add, Subtract, Multiply, and Divide Decimals to Hundredths: CCSS.Math.Content.5.NBT.B.7 - Common Core: 5th Grade Math
Card 0 of 20
Add:
![\frac{\begin{array}[b]{r}.45\ +\ .13\end{array}}{\ \ \ \ }](//cdn-s3.varsitytutors.com/uploads/formula_image/image/1087569/gif.latex)
Add:
We can use base ten blocks to help us solve this problem. Let's review what our base ten blocks are by using a whole number 

When we put this together, we add:

To use base ten blocks to add decimal numbers, we need to think of the base ten blocks a little differently. We think of the hundreds block as one whole. The tens block as tenths because you would need ten of these to make one whole. Finally, the ones block as hundredths because you would need a hundred of these to make one whole:

Let's look at this problem:
![\frac{\begin{array}[b]{r}.45\ +\ .13\end{array}}{\ \ \ \ }](//cdn-s3.varsitytutors.com/uploads/formula_image/image/1087572/gif.latex)
First, we want to represent the  with four tenths blocks and five hundredths blocks:
with four tenths blocks and five hundredths blocks:

Next, we want to represent the  with one tenths block and three hundredths blocks:
with one tenths block and three hundredths blocks:

Now, we want to combine our blocks together:

We can see that we now have five tenths blocks and eight hundredths blocks, which means our answer is 

We can use base ten blocks to help us solve this problem. Let's review what our base ten blocks are by using a whole number

When we put this together, we add:
To use base ten blocks to add decimal numbers, we need to think of the base ten blocks a little differently. We think of the hundreds block as one whole. The tens block as tenths because you would need ten of these to make one whole. Finally, the ones block as hundredths because you would need a hundred of these to make one whole:

Let's look at this problem:
First, we want to represent the 

Next, we want to represent the 

Now, we want to combine our blocks together:

We can see that we now have five tenths blocks and eight hundredths blocks, which means our answer is

Compare your answer with the correct one above
Add the following:
![\frac{\begin{array}[b]{r}.15\ +\ .32\end{array}}{\ \ \ \ }](//cdn-s3.varsitytutors.com/uploads/formula_image/image/1087576/gif.latex)
Add the following:
We can use base ten blocks to help us solve this problem. Let's review what our base ten blocks are by using a whole number 

When we put this together, we add:

To use base ten blocks to add decimal numbers, we need to think of the base ten blocks a little differently. We think of the hundreds block as one whole. The tens block as tenths because you would need ten of these to make one whole. Finally, the ones block as hundredths because you would need a hundred of these to make one whole:

Let's look at this problem:
![\frac{\begin{array}[b]{r}.15\ +\ .32\end{array}}{\ \ \ \ }](//cdn-s3.varsitytutors.com/uploads/formula_image/image/1087579/gif.latex)
First, we want to represent the  with one tenths block and five hundredths blocks:
with one tenths block and five hundredths blocks:

Next, we want to represent the  with three tenths block and two hundredths blocks:
with three tenths block and two hundredths blocks:

Now, we want to combine our blocks together:

We can see that we now have four tenths blocks and seven hundredths blocks, which means our answer is 

We can use base ten blocks to help us solve this problem. Let's review what our base ten blocks are by using a whole number

When we put this together, we add:
To use base ten blocks to add decimal numbers, we need to think of the base ten blocks a little differently. We think of the hundreds block as one whole. The tens block as tenths because you would need ten of these to make one whole. Finally, the ones block as hundredths because you would need a hundred of these to make one whole:

Let's look at this problem:
First, we want to represent the 

Next, we want to represent the 

Now, we want to combine our blocks together:

We can see that we now have four tenths blocks and seven hundredths blocks, which means our answer is

Compare your answer with the correct one above
Add:
![\frac{\begin{array}[b]{r}.56\ +\ .17\end{array}}{\ \ \ \ }](//cdn-s3.varsitytutors.com/uploads/formula_image/image/1087650/gif.latex)
Add:
We can use base ten blocks to help us solve this problem. Let's review what our base ten blocks are by using a whole number 

When we put this together, we add:

To use base ten blocks to add decimal numbers, we need to think of the base ten blocks a little differently. We think of the hundreds block as one whole. The tens block as tenths because you would need ten of these to make one whole. Finally, the ones block as hundredths because you would need a hundred of these to make one whole:

Let's look at this problem:
![\frac{\begin{array}[b]{r}.56\ +\ .17\end{array}}{\ \ \ \ }](//cdn-s3.varsitytutors.com/uploads/formula_image/image/1087653/gif.latex)
First, we want to represent the  with five tenths blocks and six hundredths blocks:
with five tenths blocks and six hundredths blocks:
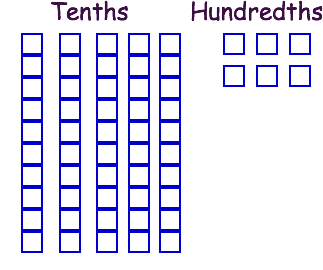
Next, we want to represent the  with one tenths block and seven hundredths blocks:
with one tenths block and seven hundredths blocks:

Now, we want to combine our blocks together:

Notice that we have more than ten hundredths blocks. This means we can take ten of the hundredths blocks and make another tenths block:


We can see that we now have seven tenths blocks and three hundredths blocks, which means our answer is 

We can use base ten blocks to help us solve this problem. Let's review what our base ten blocks are by using a whole number

When we put this together, we add:
To use base ten blocks to add decimal numbers, we need to think of the base ten blocks a little differently. We think of the hundreds block as one whole. The tens block as tenths because you would need ten of these to make one whole. Finally, the ones block as hundredths because you would need a hundred of these to make one whole:

Let's look at this problem:
First, we want to represent the 

Next, we want to represent the 

Now, we want to combine our blocks together:

Notice that we have more than ten hundredths blocks. This means we can take ten of the hundredths blocks and make another tenths block:


We can see that we now have seven tenths blocks and three hundredths blocks, which means our answer is

Compare your answer with the correct one above
Add:
![\frac{\begin{array}[b]{r}.35\ +\ .13\end{array}}{\ \ \ \ }](//vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1170419/gif.latex)
Add:
When we add decimals, we can treat it like a normal addition problem, we just need to remember out decimal:
![\frac{\begin{array}[b]{r}.35\ +\ .13\end{array}}{\ \ \ \ }](//vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1170420/gif.latex)

When we add decimals, we can treat it like a normal addition problem, we just need to remember out decimal:
Compare your answer with the correct one above
Add:
![\frac{\begin{array}[b]{r}.51\ +\ .11\end{array}}{\ \ \ \ }](//vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1170427/gif.latex)
Add:
Adding decimals is just like adding regular numbers, you just must remember to bring down your decimal point:
![\frac{\begin{array}[b]{r}.51\ +\ .11\end{array}}{\ \ \ \ }](//vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1170428/gif.latex)

Adding decimals is just like adding regular numbers, you just must remember to bring down your decimal point:
Compare your answer with the correct one above
Add:
![\frac{\begin{array}[b]{r}.24\ +\ .05\end{array}}{\ \ \ \ }](//vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1170422/gif.latex)
Add:
Adding decimals is like adding regular numbers, you just need to remember your decimal:
![\frac{\begin{array}[b]{r}.24\ +\ .05\end{array}}{\ \ \ \ }](//vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1170423/gif.latex)

Adding decimals is like adding regular numbers, you just need to remember your decimal:
Compare your answer with the correct one above
Adding decimals is just like adding whole numbers. But, you must remember your decimal in your answer.
You start adding on the far right which in this case is the hundredths place.  . We have to carry a
. We have to carry a  from the sum
from the sum  above the tenths place and place the other
above the tenths place and place the other  below the hundredths place.
below the hundredths place. 
Next, add the tenths place. 
The decimal will be carried down and remain between the tenths place and the ones place. 
The final addition portion is the ones place. 
The final answer is 
Adding decimals is just like adding whole numbers. But, you must remember your decimal in your answer.
You start adding on the far right which in this case is the hundredths place. 




Next, add the tenths place. 
The decimal will be carried down and remain between the tenths place and the ones place. 
The final addition portion is the ones place. 
The final answer is
Compare your answer with the correct one above
Adding decimals is just like adding whole numbers. But, you must remember your decimal in your answer.
You start adding on the far right which in this case is the hundredths place.  . We have to carry a
. We have to carry a  from the sum
from the sum  above the tenths place and place the
above the tenths place and place the  below the hundredths place.
below the hundredths place. 
Next, add the tenths place. 
The decimal will be carried down and remain between the tenths place and the ones place. 
The final addition portion is the ones place. 
The final answer is 
Adding decimals is just like adding whole numbers. But, you must remember your decimal in your answer.
You start adding on the far right which in this case is the hundredths place. 




Next, add the tenths place. 
The decimal will be carried down and remain between the tenths place and the ones place. 
The final addition portion is the ones place. 
The final answer is
Compare your answer with the correct one above
Adding decimals is just like adding whole numbers. But, you must remember your decimal in your answer.
You start adding on the far right which in this case is the hundredths place. 
Next, add the tenths place.  . We have to carry a
. We have to carry a  from the sum
from the sum  above the ones place and place the
above the ones place and place the  below the tenths place.
below the tenths place. 
The decimal will be carried down and remain between the tenths place and the ones place. 
The final addition portion is the ones place. 
The final answer is 
Adding decimals is just like adding whole numbers. But, you must remember your decimal in your answer.
You start adding on the far right which in this case is the hundredths place. 
Next, add the tenths place. 




The decimal will be carried down and remain between the tenths place and the ones place. 
The final addition portion is the ones place. 
The final answer is
Compare your answer with the correct one above
Adding decimals is just like adding whole numbers. But, you must remember your decimal in your answer.
You start adding on the far right which in this case is the hundredths place. 
Next, add the tenths place. 
The decimal will be carried down and remain between the tenths place and the ones place. 
The final addition portion is the ones place.  . The first
. The first  in
in  will be carried into the tens place.
will be carried into the tens place. 
The final answer is 
Adding decimals is just like adding whole numbers. But, you must remember your decimal in your answer.
You start adding on the far right which in this case is the hundredths place. 
Next, add the tenths place. 
The decimal will be carried down and remain between the tenths place and the ones place. 
The final addition portion is the ones place. 



The final answer is
Compare your answer with the correct one above
No explanation available
No explanation available
Compare your answer with the correct one above
Solve the following:

Solve the following:
We can use base ten blocks to help us solve this problem. First, we want to use base ten blocks to represent 

Because we are dividing  by
by  , we need to split up our
, we need to split up our  into groups of
into groups of 

As you can see, we have  groups; thus,
groups; thus, 
We can use base ten blocks to help us solve this problem. First, we want to use base ten blocks to represent

Because we are dividing 



As you can see, we have 
Compare your answer with the correct one above
Divide:

Divide:
We can use base ten blocks to help us solve this problem. First, we want to use base ten blocks to represent 

Because we are dividing  by
by  , we need to split up our
, we need to split up our  into groups of
into groups of  :
:

As you can see, we have  groups; thus,
groups; thus, 
We can use base ten blocks to help us solve this problem. First, we want to use base ten blocks to represent

Because we are dividing 




As you can see, we have 
Compare your answer with the correct one above
Divide:

Divide:
We can use base ten blocks to help us solve this problem. First, we want to use base ten blocks to represent 

Because we are dividing  by
by  , we need to split up our
, we need to split up our  into groups of
into groups of  :
:

As you can see, we have  groups; thus,
groups; thus, 
We can use base ten blocks to help us solve this problem. First, we want to use base ten blocks to represent

Because we are dividing 




As you can see, we have 
Compare your answer with the correct one above
Divide:

Divide:
We can use base ten blocks to help us solve this problem. First, we want to use base ten blocks to represent 

Because we are dividing  by
by  , we need to split up our
, we need to split up our  into groups of
into groups of 

We can see that we have 2 groups of 2, thus the answer is 2.
We can use base ten blocks to help us solve this problem. First, we want to use base ten blocks to represent

Because we are dividing 



We can see that we have 2 groups of 2, thus the answer is 2.
Compare your answer with the correct one above
Divide:

Divide:
We can use base ten blocks to help us solve this problem. First, we want to use base ten blocks to represent 

Because we are dividing by
by  , we need to split up our
, we need to split up our  into groups of
into groups of 

As you can see, we have  groups. Thus the answer is
groups. Thus the answer is  .
.
We can use base ten blocks to help us solve this problem. First, we want to use base ten blocks to represent

Because we are dividing



As you can see, we have 

Compare your answer with the correct one above
Divide:

Divide:
We can use base ten blocks to help us solve this problem. First, we want to use base ten blocks to represent .2

Because we are dividing .2 by .2, we need to split up our .2 into groups of .2:

We can see that we have 1 group, thus our answer is 1.
We can use base ten blocks to help us solve this problem. First, we want to use base ten blocks to represent .2

Because we are dividing .2 by .2, we need to split up our .2 into groups of .2:

We can see that we have 1 group, thus our answer is 1.
Compare your answer with the correct one above

The problem that you are challenged to solve is  .
.
 is the dividend, this is what is being broken up into groups.
is the dividend, this is what is being broken up into groups.  is our divisor which is the number of groups you are making. We need to split
is our divisor which is the number of groups you are making. We need to split  in half to see how many are in each group.
in half to see how many are in each group.
The first step is to place your decimal above your equation in the same place. It will line up with the decimal inside of your "long-division house".

Next, we need to use or multiplication facts to determine what  can be multiplied by to make
can be multiplied by to make  or get close to it without going over.
or get close to it without going over.  is the fact that works best (
is the fact that works best ( is too large). We will place the numeral
is too large). We will place the numeral  directly above the
directly above the  in the ones place to indicate that
in the ones place to indicate that  groups of
groups of  fit into the
fit into the  . We will put the product of
. We will put the product of  which was
which was  underneath the
underneath the  in the ones place and subtract the difference. The numbers above the "house" are our quotient or answer to the division problem.
in the ones place and subtract the difference. The numbers above the "house" are our quotient or answer to the division problem.

Next, we will carry the  in the tenths place down and put it next to the
in the tenths place down and put it next to the  . We will work with the numbers as if they were
. We will work with the numbers as if they were  when thinking of multiplication facts, but it should be noted this is actually
when thinking of multiplication facts, but it should be noted this is actually  when you consider the decimal placement.
when you consider the decimal placement.  so we place the
so we place the  above the "house" in the tenths place of our quotient and subtract the
above the "house" in the tenths place of our quotient and subtract the  . We are left with
. We are left with  remaining so there is no remainder.
remaining so there is no remainder.

Our final answer is  , which means that half of
, which means that half of  is
is 
The problem that you are challenged to solve is 



The first step is to place your decimal above your equation in the same place. It will line up with the decimal inside of your "long-division house".

Next, we need to use or multiplication facts to determine what 












Next, we will carry the 








Our final answer is 

Compare your answer with the correct one above

The problem that you are challenged to solve is  .
.

 is the dividend, this is what is being broken up into groups.
is the dividend, this is what is being broken up into groups.  is our divisor which is the number of groups you are making. We need to split
is our divisor which is the number of groups you are making. We need to split  in thirds to see how many are in each group.
in thirds to see how many are in each group.
The first step is to place your decimal above your equation in the same place. It will line up with the decimal inside of your "long-division house".

Next, we need to use or multiplication facts to determine what  can be multiplied by to make
can be multiplied by to make  or get close to it without going over.
or get close to it without going over.  is the fact that works best (
is the fact that works best ( is too large). We will place the numeral
is too large). We will place the numeral  directly above the
directly above the  in the ones place to indicate that
in the ones place to indicate that  groups of
groups of  fit into the
fit into the  . We will put the product of
. We will put the product of  which was
which was  underneath the
underneath the  and subtract the difference. The numbers above the "house" are our quotient or answer to the division problem.
and subtract the difference. The numbers above the "house" are our quotient or answer to the division problem.

Next, we will carry the  in the tenths place down and put it next to the
in the tenths place down and put it next to the  . We will work with the numbers as if they were
. We will work with the numbers as if they were  when thinking of multiplication facts, but it should be noted this is actually
when thinking of multiplication facts, but it should be noted this is actually  when you consider the decimal placement.
when you consider the decimal placement.  so we place the
so we place the  above the "house" in the tenths place of our quotient and subtract the
above the "house" in the tenths place of our quotient and subtract the  . We are left with
. We are left with  remaining.
remaining.

Finally, we carry down the  from the hundredths place and place it next to the
from the hundredths place and place it next to the  giving us
giving us  (or
(or  for the purpose of our multiplication facts.)
for the purpose of our multiplication facts.)  so we place the
so we place the  above the
above the  in the hundredths place on top of our "house" and subtract the
in the hundredths place on top of our "house" and subtract the  leaving us with a remainder of
leaving us with a remainder of  .
.

Our final answer is 
The problem that you are challenged to solve is 




The first step is to place your decimal above your equation in the same place. It will line up with the decimal inside of your "long-division house".

Next, we need to use or multiplication facts to determine what 












Next, we will carry the 








Finally, we carry down the 









Our final answer is
Compare your answer with the correct one above

The problem that you are challenged to solve is  .
.

 is the dividend, this is what is being broken up into groups.
is the dividend, this is what is being broken up into groups.  is our divisor which is the number of groups you are making. We need to split
is our divisor which is the number of groups you are making. We need to split  in quarters to see how many are in each group.
in quarters to see how many are in each group.
The first step is to place your decimal above your equation in the same place. It will line up with the decimal inside of your "long-division house".

Next, we need to use or multiplication facts to determine what  can be multiplied by to make
can be multiplied by to make  or get close to it without going over.
or get close to it without going over.  is the fact that works best. We will place the numeral
is the fact that works best. We will place the numeral  directly above the
directly above the  in the ones place to indicate that
in the ones place to indicate that  groups of
groups of  fit into the
fit into the  . We will put the product of
. We will put the product of  which was
which was  underneath the
underneath the  and subtract the difference. The numbers above the "house" are our quotient or answer to the division problem.
and subtract the difference. The numbers above the "house" are our quotient or answer to the division problem.

Next, we will carry the  in the tenths place down and put it next to the
in the tenths place down and put it next to the  .
.  so we place the
so we place the  above the "house" in the tenths place of our quotient and subtract the
above the "house" in the tenths place of our quotient and subtract the  . We are left with
. We are left with  remaining.
remaining.

Finally, we carry down the  from the hundredths place and place it next to the
from the hundredths place and place it next to the  .
.  so we place the
so we place the  above the
above the  in the hundredths place on top of our "house" and subtract the
in the hundredths place on top of our "house" and subtract the  leaving us with a remainder of
leaving us with a remainder of  .
.

Our final answer is 
The problem that you are challenged to solve is 




The first step is to place your decimal above your equation in the same place. It will line up with the decimal inside of your "long-division house".

Next, we need to use or multiplication facts to determine what 











Next, we will carry the 






Finally, we carry down the 







Our final answer is
Compare your answer with the correct one above
![\frac{\begin{array}[b]{r}.45\ +\ .13\end{array}}{\ \ \ \ }](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1087569/gif.latex)


![\frac{\begin{array}[b]{r}.45\ +\ .13\end{array}}{\ \ \ \ }](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1087572/gif.latex)

![\frac{\begin{array}[b]{r}.15\ +\ .32\end{array}}{\ \ \ \ }](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1087576/gif.latex)


![\frac{\begin{array}[b]{r}.15\ +\ .32\end{array}}{\ \ \ \ }](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1087579/gif.latex)

![\frac{\begin{array}[b]{r}.56\ +\ .17\end{array}}{\ \ \ \ }](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1087650/gif.latex)


![\frac{\begin{array}[b]{r}.56\ +\ .17\end{array}}{\ \ \ \ }](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1087653/gif.latex)

![\frac{\begin{array}[b]{r}.35\ +\ .13\end{array}}{\ \ \ \ }](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1170419/gif.latex)
![\frac{\begin{array}[b]{r}.35\ +\ .13\end{array}}{\ \ \ \ }](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1170420/gif.latex)

![\frac{\begin{array}[b]{r}.51\ +\ .11\end{array}}{\ \ \ \ }](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1170427/gif.latex)
![\frac{\begin{array}[b]{r}.51\ +\ .11\end{array}}{\ \ \ \ }](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1170428/gif.latex)

![\frac{\begin{array}[b]{r}.24\ +\ .05\end{array}}{\ \ \ \ }](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1170422/gif.latex)
![\frac{\begin{array}[b]{r}.24\ +\ .05\end{array}}{\ \ \ \ }](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1170423/gif.latex)

![\frac{\begin{array}[b]{r}7.17\ +\ 2.24\end{array}}{\ \ \ \ }](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1177883/gif.latex)

![\frac{\begin{array}[b]{r}3.64\ +\ 2.26\end{array}}{\ \ \ \ }](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1177871/gif.latex)

![\frac{\begin{array}[b]{r}0.84\ +\ 0.64\end{array}}{\ \ \ \ }](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1177877/gif.latex)

![\frac{\begin{array}[b]{r}8.13\ +\ 2.34\end{array}}{\ \ \ \ }](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1177897/gif.latex)





















