Solve Two-Step Word Problems Using the Four Operations: CCSS.Math.Content.3.OA.D.8 - Common Core: 3rd Grade Math
Card 0 of 15
In Spot’s toy basket he has 
balls. There are 
more stuffed animals than balls and there is double the number of ropes than balls. How many toys does Spot have in his basket?
In Spot’s toy basket he has
To solve this problem, we first have to find our unknowns. Our unknowns are the number of ropes and stuffed animals that Spot has. We can set up equations for these unknowns by letting 
represent ropes and 
represent stuffed animals.
because he has 
more stuffed animals than his 
balls.
because double means 
times more.
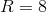
Now we need to add up our number of balls, stuffed animals and ropes to find our total.
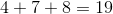
To solve this problem, we first have to find our unknowns. Our unknowns are the number of ropes and stuffed animals that Spot has. We can set up equations for these unknowns by letting
Now we need to add up our number of balls, stuffed animals and ropes to find our total.
Compare your answer with the correct one above
In Spot’s toy basket he has 
balls. There are 
more stuffed animals than balls and there is five times the number of ropes than balls. How many toys does Spot have in his basket?
In Spot’s toy basket he has
To solve this problem, we first have to find our unknowns. Our unknowns are the number of ropes and stuffed animals that Spot has. We can set up equations for these unknowns by letting 
represent ropes and 
represent stuffed animals.
because he has 
more stuffed animals than his 
balls.
because he has five times as many ropes as his 
balls.
Now we need to add up our number of balls, stuffed animals and ropes to find our total.
To solve this problem, we first have to find our unknowns. Our unknowns are the number of ropes and stuffed animals that Spot has. We can set up equations for these unknowns by letting
Now we need to add up our number of balls, stuffed animals and ropes to find our total.
Compare your answer with the correct one above
Jessica has been collecting beads all summer. She started with 
beads and by the end of the summer she was able to add 
more beads to her collection. On the first day of school she wants to evenly split the beads up amongst her 
friends. How many beads will each friend get?
Jessica has been collecting beads all summer. She started with
To solve this problem, we first have to find our unknowns. Our unknowns are the number of beads she will have by the end of the summer and the number of beads each of her friends will receive. We can set up equations for these unknowns by letting 
represent the beads that she has at the end of the summer and 
represent the number of beads each of her friends will receive.
because she gets 
more beads by the end of the summer.
because she is splitting up her total amount of beads between 
friends. When you split something up evenly you divide.
To solve this problem, we first have to find our unknowns. Our unknowns are the number of beads she will have by the end of the summer and the number of beads each of her friends will receive. We can set up equations for these unknowns by letting
Compare your answer with the correct one above
Emily has been collecting beads all summer. She started with 
beads and by the end of the summer she was able to add 
more beads to her collection. On the first day of school she wants to evenly split the beads up amongst her 
friends. How many beads will each friend get?
Emily has been collecting beads all summer. She started with
To solve this problem, we first have to find our unknowns. Our unknowns are the number of beads she will have by the end of the summer and the number of beads each of her friends will receive. We can set up equations for these unknowns by letting 
represent the beads that she has at the end of the summer and 
represent the number of beads each of her friends will receive.
because she gets 
more beads by the end of the summer.
because she is splitting up her total amount of beads between 
friends. When you split something up evenly you divide.
To solve this problem, we first have to find our unknowns. Our unknowns are the number of beads she will have by the end of the summer and the number of beads each of her friends will receive. We can set up equations for these unknowns by letting
Compare your answer with the correct one above
Sara is hanging up flyers around her school. She started with 
flyers. She hung 
flyers around the east side of the building, but she hung half as many flyers on the west side of the building. How many flyers does she have left?
Sara is hanging up flyers around her school. She started with
To solve this problem, we first have to find our unknowns. Our unknowns are the number of flyers that she hung on the west side of the building and the number of flyers she has left over. We can set up equations for these unknowns by letting 
represent the flyers she hung on the west side and 
represent the flyers that she has left.
because she hung half as many flyers on the west side as she hung on the east side. When we half something we always divide by 
.
To find the total number of flyers that she hung we add the amount of flyers on the east side and the amount on the west side.
To find how many flyers she has left, we subtract that total flyers that were hung from the 
flyers that she started with.
To solve this problem, we first have to find our unknowns. Our unknowns are the number of flyers that she hung on the west side of the building and the number of flyers she has left over. We can set up equations for these unknowns by letting
To find the total number of flyers that she hung we add the amount of flyers on the east side and the amount on the west side.
To find how many flyers she has left, we subtract that total flyers that were hung from the
Compare your answer with the correct one above
Ali is hanging up flyers around her school. She started with 
flyers. She hung 
flyers around the east side of the building, but she hung half as many flyers on the west side of the building. How many flyers does she have left?
Ali is hanging up flyers around her school. She started with
To solve this problem, we first have to find our unknowns. Our unknowns are the number of flyers that she hung on the west side of the building and the number of flyers she has left over. We can set up equations for these unknowns by letting 
represent the flyers she hung on the west side and 
represent the flyers that she has left.
because she hung half as many flyers on the west side as she hung on the east side. When we half something we always divide by 
.
To find the total number of flyers that she hung we add the amount of flyers on the east side and the amount on the west side.
To find how many flyers she has left, we subtract that total flyers that were hung from the 
flyers that she started with.
To solve this problem, we first have to find our unknowns. Our unknowns are the number of flyers that she hung on the west side of the building and the number of flyers she has left over. We can set up equations for these unknowns by letting
To find the total number of flyers that she hung we add the amount of flyers on the east side and the amount on the west side.
To find how many flyers she has left, we subtract that total flyers that were hung from the
Compare your answer with the correct one above
Charlie swims laps in the pool every day during the week before school. On Monday and Tuesday he swims 
laps each day. On Wednesday and Thursday he triples the number of laps he swims. By Friday, he does 
less laps than he does on Monday. How many total laps does he swim during the week?
Charlie swims laps in the pool every day during the week before school. On Monday and Tuesday he swims
To solve this problem, we first have to find our unknowns. Our unknowns are the number of laps he swims on Wednesday and Thursday and the number of laps he swims on Friday. We can set up equations for these unknowns by letting 
represent the laps that he swims on Wednesday and Thursday and 
represent the number of laps he swims on Friday.
because when we triple something we multiply by 
.
because he is swimming 
less laps than he did on Monday, which means we subtract.
To find the total amount of laps that he swam, we need to add up the laps that he did each day.
To solve this problem, we first have to find our unknowns. Our unknowns are the number of laps he swims on Wednesday and Thursday and the number of laps he swims on Friday. We can set up equations for these unknowns by letting
To find the total amount of laps that he swam, we need to add up the laps that he did each day.
Compare your answer with the correct one above
Tim swims laps in the pool every day during the week before school. On Monday and Tuesday he swims 
laps each day. On Wednesday and Thursday he doubles the number of laps he swims. On Friday, he swims 
fewer laps than he swam on Monday. How many total laps does he swim during the week?
Tim swims laps in the pool every day during the week before school. On Monday and Tuesday he swims
To solve this problem, we first have to find our unknowns. Our unknowns are the number of laps he swims on Wednesday and Thursday and the number of laps he swims on Friday. We can set up equations for these unknowns by letting 
represent the laps that he swims on Wednesday and Thursday and 
represent the number of laps he swims on Friday.
because when we double something we multiply by 
.
because he is swimming 
less laps than he did on Monday, which means we subtract.
To find the total amount of laps that he swam, we need to add up the laps that he did each day.
To solve this problem, we first have to find our unknowns. Our unknowns are the number of laps he swims on Wednesday and Thursday and the number of laps he swims on Friday. We can set up equations for these unknowns by letting
To find the total amount of laps that he swam, we need to add up the laps that he did each day.
Compare your answer with the correct one above
Justin loves to run and is training for a marathon at the end of the month. His training program has him running 
miles three times during the week, and 
miles on a weekend day. How many miles does he run in a week?
Justin loves to run and is training for a marathon at the end of the month. His training program has him running
To solve this problem, we first have to find our unknowns. Our unknowns are the number of miles he runs during the week and the total miles that he runs. We can set up equations for these unknowns by letting 
represent the miles that he runs during the weekdays and 
represent the total miles that he runs in 
week.
because he is running 
miles 
times.
because to find the total we need to add the miles he runs during the week and on the weekend.
To solve this problem, we first have to find our unknowns. Our unknowns are the number of miles he runs during the week and the total miles that he runs. We can set up equations for these unknowns by letting
Compare your answer with the correct one above
Jason loves to run and is training for a marathon at the end of the month. His training program has him running 
miles three times a week, and 
miles one time a week. How many miles does he run in a week?
Jason loves to run and is training for a marathon at the end of the month. His training program has him running
To solve this problem, we first have to find our unknowns. Our unknowns are the number of miles he runs during the week and the total miles that he runs. We can set up equations for these unknowns by letting 
represent the miles that he runs during the weekdays and 
represent the total miles that he runs in 
week.
because he is running 
miles 
times.
because to find the total we need to add the miles he runs during the week and on the weekend.
To solve this problem, we first have to find our unknowns. Our unknowns are the number of miles he runs during the week and the total miles that he runs. We can set up equations for these unknowns by letting
Compare your answer with the correct one above
Hannah is making a red fruit salad because red is her favorite color. She cuts up 
pieces of watermelon and puts it in a bowl. Because she really loves strawberries, she wants 
times as many pieces of strawberries as pieces of watermelon. Then she adds half as many raspberries as strawberries. How many pieces of fruit are in her fruit salad?
Hannah is making a red fruit salad because red is her favorite color. She cuts up
To solve this problem, we first have to find our unknowns. Our unknowns are the number strawberries and raspberries she puts in the fruit salad. We can set up equations for these unknowns by letting 
represent strawberries and 
represent raspberries.
because she has 
times as many strawberries than watermelon.
because when we half something we always divide by 
Now we need to add the watermelon, strawberries, and raspberries together to find our total.
To solve this problem, we first have to find our unknowns. Our unknowns are the number strawberries and raspberries she puts in the fruit salad. We can set up equations for these unknowns by letting
Now we need to add the watermelon, strawberries, and raspberries together to find our total.
Compare your answer with the correct one above
Hannah is making a red fruit salad because red is her favorite color. She cuts up 
pieces of watermelon and puts it in a bowl. Because she really loves strawberries, she wants 
times as many pieces of strawberries as pieces of watermelon. Then she adds half as many raspberries as strawberries. How many pieces of fruit are in her fruit salad?
Hannah is making a red fruit salad because red is her favorite color. She cuts up
To solve this problem, we first have to find our unknowns. Our unknowns are the number strawberries and raspberries she puts in the fruit salad. We can set up equations for these unknowns by letting 
represent strawberries and 
represent raspberries.
because she has 
times as many strawberries than watermelon.
because when we half something we always divide by 
Now we need to add the watermelon, strawberries, and raspberries together to find our total.
To solve this problem, we first have to find our unknowns. Our unknowns are the number strawberries and raspberries she puts in the fruit salad. We can set up equations for these unknowns by letting
Now we need to add the watermelon, strawberries, and raspberries together to find our total.
Compare your answer with the correct one above
There were 
families of meerkats that lived in the same burrows. Each family had 
meerkats. 
meerkats went out to find food, how many are left in the burrows?
There were 
To solve this problem, we first have to find our unknowns. Our unknowns are how many meerkats there are total (T) and how many meerkats are left in the burrow (L).
because there are 
families of meerkats and each of them has 
members of the family. Each is a keyword for multiplication so that gives us a hint.
because there are 
meerkats total in the burrows and 
meerkats are subtracted because they left the burrow.
There are 
meerkats left in the burrows.
To solve this problem, we first have to find our unknowns. Our unknowns are how many meerkats there are total (T) and how many meerkats are left in the burrow (L).
There are 
Compare your answer with the correct one above
Patrick got 
baseball trading cards for his birthday from his best friend. The next day he received 
more cards from his uncle. He decided to share them equally between himself and his two brothers. How many cards will each child receive?
Patrick got 
To solve this problem, we first have to find our unknowns. Our unknowns are how many baseball cards Patrick received in total (T) and how many cards each child will receive (C).
because he received 
cards from his friend and then another 
from his uncle. The cards would be added together to find the total.
÷
because there are 
cards total and they are being shared equally among Patrick AND his two brothers so there are 
children total. "Shared equally" is a keyword for division.
Each child will receive 
cards in total.
To solve this problem, we first have to find our unknowns. Our unknowns are how many baseball cards Patrick received in total (T) and how many cards each child will receive (C).
Each child will receive 
Compare your answer with the correct one above
In Denver, it snowed 5 inches on Monday, 6 inches on Tuesday, 3 inches on Thursday, and 1 inch on Friday. On Saturday, it snowed three times as much as the rest of the week. How much did it snow on Saturday?
In Denver, it snowed 5 inches on Monday, 6 inches on Tuesday, 3 inches on Thursday, and 1 inch on Friday. On Saturday, it snowed three times as much as the rest of the week. How much did it snow on Saturday?
To solve this problem, we first have to find our unknowns. Our unknowns are how much did it snow during the weekdays (W) and how much did it snow on Saturday (S).
because we need to know how much it snowed during the weekdays in total. We must add together the amount of snow from Monday, Tuesday, Thursday, and Friday.
because it snowed 
times as much on Saturday as it did the rest of the week. The total snow from the weekdays will be multiplied by 
to find out how much it snowed on Saturday.
On Saturday it snowed a total of 
inches.
To solve this problem, we first have to find our unknowns. Our unknowns are how much did it snow during the weekdays (W) and how much did it snow on Saturday (S).
On Saturday it snowed a total of 
Compare your answer with the correct one above